matlab分水岭算法分割图像的结果说明_图像分割-分水岭算法
分水岭(Watershed)是基于地理形态的分析的图像分割算法,模仿地理结构(比如山川、沟壑,盆地)来实现对不同物体的分类。
分水岭算法中会用到一个重要的概念——测地线距离。
测地线距离(Geodesic Distance)
测地线距离就是地球表面两点之间的最短路径(可执行路径)的距离,在图论中,Geodesic Distance 就是图中两节点的最短路径的距离,这与平时在几何空间通常用到的 Euclidean Distance(欧氏距离),即两点之间的最短距离有所区别。
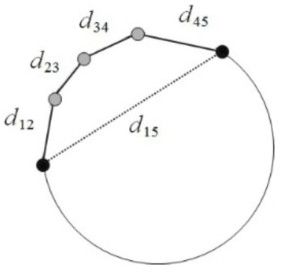
在下图中,两个黑点的 Euclidean Distance 是用虚线所表示的线段的长度
在三维曲面空间中两点间的测地距离就是两点间沿着三维曲面的表面走的最短路径。
分水岭算法
图像的灰度空间很像地球表面的整个地理结构,每个像素的灰度值代表高度。其中的灰度值较大的像素连成的线可以看做山脊,也就是分水岭。其中的水就是用于二值化的gray threshold level,二值化阈值可以理解为水平面,比水平面低的区域会被淹没,刚开始用水填充每个孤立的山谷(局部最小值)。
当水平面上升到一定高度时,水就会溢出当前山谷,可以通过在分水岭上修大坝,从而避免两个山谷的水汇集,这样图像就被分成2个像素集,一个是被水淹没的山谷像素集,一个是分水岭线像素集。最终这些大坝形成的线就对整个图像进行了分区,实现对图像的分割。
图2在该算法中,空间上相邻并且灰度值相近的像素被划分为一个区域。
分水岭算法的整个过程:
- 把梯度图像中的所有像素按照灰度值进行分类,并设定一个测地距离阈值。
- 找到灰度值最小的像素点(默认标记为灰度值最低点),让threshold从最小值开始增长,这些点为起始点。
- 水平面在增长的过程中,会碰到周围的邻域像素,测量这些像素到起始点(灰度值最低点)的测地距离,如果小于设定阈值,则将这些像素淹没,否则在这些像素上设置大坝,这样就对这些邻域像素进行了分类。
4. 随着水平面越来越高,会设置更多更高的大坝,直到灰度值的最大值,所有区域都在分水岭线上相遇,这些大坝就对整个图像像素的进行了分区。
整个过程可以查看下面这个动图:
图4用上面的算法对图像进行分水岭运算,由于噪声点或其它因素的干扰,可能会得到密密麻麻的小区域,即图像被分得太细(over-segmented,过度分割),这因为图像中有非常多的局部极小值点,每个点都会自成一个小区域。
其中的解决方法:
- 对图像进行高斯平滑操作,抹除很多小的最小值,这些小分区就会合并。
- 不从最小值开始增长,可以将相对较高的灰度值像素作为起始点(需要用户手动标记),从标记处开始进行淹没,则很多小区域都会被合并为一个区域,这被称为基于图像标记(mark)的分水岭算法。
下面三个图分别是原图,分水岭过分割的图以及基于标记的分水岭算法得到的图:
图5其中标记的每个点就相当于分水岭中的注水点,从这些点开始注水使得水平面上升,但是如上图所示,图像中需要分割的区域太多了,手动标记太麻烦,我们可是使用距离转换的方法进行标记,OpenCV中就是使用的这种方法。
OpenCV中分水岭算法
在OpenCV中,我们需要给不同区域贴上不同的标签。用大于1的整数表示我们确定为前景或对象的区域,用1表示我们确定为背景或非对象的区域,最后用0表示我们无法确定的区域。然后应用分水岭算法,我们的标记图像将被更新,更新后的标记图像的边界像素值为-1。
下面对相互接触的硬币应用距离变换和分水岭分割。
图6先使用 Otsu's 二值化对图像进行二值化。
import cv2
import numpy as np
img = cv2.imread('coins.png')
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
ret, thresh = cv2.threshold(gray, 0, 255, cv2.THRESH_BINARY_INV+cv2.THRESH_OTSU)先使用开运算去除图像中的细小白色噪点,然后通过腐蚀运算移除边界像素,得到的图像中的白色区域肯定是真实前景,即靠近硬币中心的区域(下面左边的图);膨胀运算使得一部分背景成为了物体到的边界,得到的图像中的黑色区域肯定是真实背景,即远离硬币的区域(下面中间的图)。
剩下的区域(硬币的边界附近)还不能确定是前景还是背景。可通过膨胀图减去腐蚀图得到,下图中的白色部分为不确定区域(下面右边的图)。
# noise removal
kernel = cv2.getStructuringElement(cv2.MORPH_RECT, (3,3))
opening = cv2.morphologyEx(thresh, cv2.MORPH_OPEN, kernel, iterations=2)
sure_bg = cv2.dilate(opening, kernel, iterations=2) # sure background area
sure_fg = cv2.erode(opening, kernel, iterations=2) # sure foreground area
unknown = cv2.subtract(sure_bg, sure_fg) # unknown area剩下的区域不确定是硬币还是背景,这些区域通常在前景和背景接触的区域(或者两个不同硬币接触的区域),我们称之为边界。通过分水岭算法应该能找到确定的边界。
由于硬币之间彼此接触,我们使用另一个确定前景的方法,就是带阈值的距离变换。
下面左边的图为得到的距离转换图像,其中每个像素的值为其到最近的背景像素(灰度值为0)的距离,可以看到硬币的中心像素值最大(中心离背景像素最远)。对其进行二值处理就得到了分离的前景图(下面中间的图),白色区域肯定是硬币区域,而且还相互分离,下面右边的图为之前的膨胀图减去中间这个表示前景的图。
# Perform the distance transform algorithm
dist_transform = cv2.distanceTransform(opening, cv2.DIST_L2, 5)
# Normalize the distance image for range = {0.0, 1.0}
cv2.normalize(dist_transform, dist_transform, 0, 1.0, cv2.NORM_MINMAX)
# Finding sure foreground area
ret, sure_fg = cv2.threshold(dist_transform, 0.5*dist_transform.max(), 255, 0)
# Finding unknown region
sure_fg = np.uint8(sure_fg)
unknown = cv2.subtract(sure_bg,sure_fg)现在我们可以确定哪些是硬币区域,哪些是背景区域。然后创建标记(marker,它是一个与原始图像大小相同的矩阵,int32数据类型),表示其中的每个区域。分水岭算法将标记的0的区域视为不确定区域,将标记为1的区域视为背景区域,将标记大于1的正整数表示我们想得到的前景。
我们可以使用 cv2.connectedComponents() 来实现这个功能,它是用0标记图像的背景,用大于0的整数标记其他对象。所以我们需要对其进行加一,用1来标记图像的背景。
cv2.connectedComponents() 将传入图像中的白色区域视为组件(前景)。
# Marker labelling
ret, markers = cv2.connectedComponents(sure_fg)
# Add one to all labels so that sure background is not 0, but 1
markers = markers+1
# Now, mark the region of unknown with zero
markers[unknown==255] = 0注意:得到的markers矩阵的元素类型为 int32,要使用 imshow() 进行显示,需要将其转换为 uint8 类型( markers=np.uint8(markers) )。
我们对得到的markers进行显示:
markers_copy = markers.copy()
markers_copy[markers==0] = 150 # 灰色表示背景
markers_copy[markers==1] = 0 # 黑色表示背景
markers_copy[markers>1] = 255 # 白色表示前景
markers_copy = np.uint8(markers_copy)标记图像已经完成了,最后应用分水岭算法。然后标记图像将被修改,边界区域将被标记为-1。
# 使用分水岭算法执行基于标记的图像分割,将图像中的对象与背景分离
markers = cv2.watershed(img, markers)
img[markers==-1] = [0,0,255] # 将边界标记为红色经过分水岭算法得到的新的标记图像和分割后的图像如下图所示:
图11任何两个相邻连接的组件不一定被分水岭边界(-1的像素)分开;例如在传递给 watershed 函数的初始标记图像中的物体相互接触。
总结
我们通过一个例子介绍了分水岭算法的整个过程,主要分为以下几步:
- 对图进行灰度化和二值化得到二值图像
- 通过膨胀得到确定的背景区域,通过距离转换得到确定的前景区域,剩余部分为不确定区域
- 对确定的前景图像进行连接组件处理,得到标记图像
- 根据标记图像对原图像应用分水岭算法,更新标记图像
参考:
OpenCV Watershed Algorithm
IMAGE SEGMENTATION AND MATHEMATICAL MORPHOLOGY
Classic Watershed
基于标记的分水岭分割算法/OpenCV中距离变换
剪刀手/分水岭分割法
The Watershed Transform
对扑克牌应用分水岭的例子