分类算法——逻辑回归

分类算法

说到分类算法，不能不提到的就是Logistics Regressio(以下均称逻辑回归)

个人认为逻辑回归在分类算法中有着非常重要的地位，因此会花很大的篇幅总结逻辑回归模型。

逻辑回归的模型构建

1. 广义线性模型

为了解决线性回归本身线性结构的局限性，人们在线性回归的基础上在等号的左边或右边加上一个函数，从而更好的捕捉数据的一般规律，此时这种模型就被称为广义线性模型，上面提及的函数被称为联系函数。

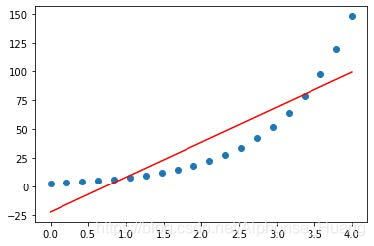
有这么一组数据集，假设数据之间的关系是
$$y=e^{x+1}$$
若此时以线性方程来预测，即
$$y=\omega \cdot x+b$$
则此时模型本身与数据本身的拟合如下图

可以发现，线性模型预测结果和真实结果差距较大。但此时如果我们在等号右边加上以为底的指数运算，也就是将线性方程输出结果进行以为底的指数运算转换之后去预测y，即将方程改写为

$$y=e^{\omega \cdot x}$$

等价于
$$\ln y={\omega }^T\cdot x$$

即相当于是线性方程输出结果去预测取以为底的对数运算之后的结果。

通过上面的过程，我们不难发现，通过在模型左右两端加上某些函数，能够让线性模型也具备捕捉非线性规律的能力。而在上例中，这种捕捉非线性规律的本质，是在方程加入对数函数之后，能够使得模型的输入空间（特征所在空间）到输出空间（标签所在空间）进行了非线性的函数映射。而这种连接线性方程左右两端、并且实际上能够拓展模型性能的函数，就被称为联系函数，而加入了联系函数的模型也被称为广义线性模型。广义线性模型的一般形式可表示如下：

$$g(y)={\omega }^T\cdot x$$

等价于

$$y=g^{-1}({\omega }^T\cdot x)$$

2.对数几率模型

• 几率（odd）与对数几率

  几率不是概率，而是一个事件发生与不发生的概率的比值。假设某事件发生的概率为p，则该事件不发生的概率为1-p，该事件的几率为：
  $$odd(p)=\frac{p}{1-p}$$

  在几率的基础上取（自然底数的）对数，则构成该事件的对数几率（logit）
  $$logit(p)=\ln \frac{p}{1-p}$$

• 对数几率模型

  我们将对数几率看成是一个函数，并将其作为联系函数，即$g(y)=\ln \frac{y}{1-y}$，则该广义线性模型为：

  $$g(y)=\ln \frac{y}{1-y}={\omega }^T\cdot x$$

  此时模型就被称为对数几率回归（logistic regression），也被称为逻辑回归。

---

进一步地，如果我们想将上述的对数几率模型“反解”出来，就是改成$y=f(x)$的形式，即有

原式子:
$$\ln \frac{y}{1-y}={\omega }^T\cdot x$$

一步变换:
$$\frac{y}{1-y}=e^{{\omega }^T\cdot x}$$

经过一系列变换:
$$y=\frac{1}{1+e^{-{\omega }^T\cdot x}}=g^{-1}({\omega }^T\cdot x)$$

最后得到逻辑回归的模型为:
$$y=\frac{1}{1+e^{-{\omega }^T\cdot x}}$$

同时也可以看到，对数几率函数的反函数为
$$f(x)=\frac{1}{1+e^{-x}}$$

同时$f(x)$也被成为$sigmoid$函数。

3.逻辑回归模型输出结果与模型可解释性

从整体情况来看，逻辑回归在经过$Sigmoid$函数处理之后，是将线性方程输出结果压缩在了0-1之间，用该结果再来进行回归类的连续数值预测肯定是不合适的了。在实际模型应用过程中，
逻辑回归主要应用于二分类问题的预测。

逻辑回归输出结果$y$是否是概率?

 
决定y是否是概率的核心因素，不是模型本身，而是建模流程。
 
$Logistics$本身也有对应的概率分布，因此输入的自变量其实是可以视作随机变量的，但前提是需要满足一定的分布要求。
 
如果逻辑回归的建模流程遵照数理统计方法的一般建模流程，即自变量的分布（或者转化之后的分布）满足一定要求（通过检验），则最终模型输出结果就是严格意义上的概率取值。
 
而如果是遵照机器学习建模流程进行建模，在为对自变量进行假设检验下进行模型构建，则由于自变量分布不一定满足条件，因此输出结果不一定为严格意义上的概率。

或者说，根据逻辑回归方程
$$y=\frac{1}{1+e^{-(1-x)}}$$

进一步推导得出：
$$\ln \frac{y}{1-y}=1-x$$

可以解读为 $x$每增加1，样本属于1的概率的对数几率就减少1。

而这种基于自变量系数的可解释性不仅可以用于自变量和因变量之间的解释，还可用于自变量重要性的判别当中，例如，假设逻辑回归方程如下：

$$\ln \frac{y}{1-y}=x_1+3x_2-1$$

可解读为$x_2$的重要性是$x_1$的3倍.

4.多分类逻辑回归

前面的讨论都是基于二分类问题（0-1分类问题）展开的讨论，而如果要使用逻辑回归解决多分类，则需要额外掌握一些技术手段。

总的来说，如果要使用逻辑回归解决多分类问题，一般来说有两种方法

• 其一是将逻辑回归模型改为多分类模型形式
• 其二则是采用通用的多分类学习方法对建模流程进行改造

其中将逻辑回归模型改写成多分类模型形式并不常用并且求解过程非常复杂，包括Scikit-Learn在内，主流的实现多分类逻辑回归的方法都是采用多分类学习方法。所谓多分类学习方法，则指的是将一些二分类学习器（binary classifier）推广到多分类的场景中，该方法属于包括逻辑回归在内所有二分类器都能使用的通用方法。

多分类问题的一般解决思路

用二分类学习器解决多分类问题的基本思想是先拆分后集成

1. 先将数据集进行拆分
2. 然后多个数据集可训练多个模型
3. 最后再对多个模型进行集成。这里所谓集成，指的是使用这多个模型对后续新进来数据的预测方法。

Example-四分类问题

具体来看，主要有三种策略

• “一对一”(One vs One, OvO)

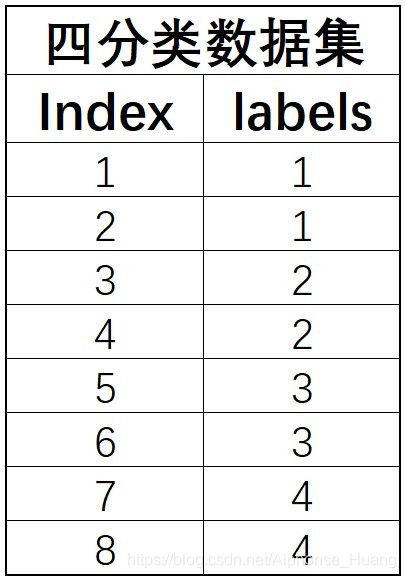
  OvO的拆分策略比较简单，基本过程是将每个类别对应数据集单独拆分成一个子数据集，然后令其两两组合，再来进行模型训练。例如，对于上述四分类数据集，根据标签类别可将其拆分成四个数据集，然后再进行两两组合，总共有6种组合，也就是
  种组合。拆分过程如下所示：
  

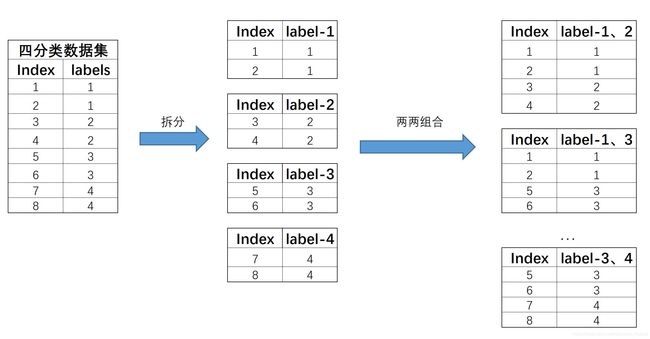
  而后在这6个新和成的数据集上，我们就能训练6个分类器。

  当模型训练完成之后，接下来面对新数据集的预测，可以使用投票法从6个分类器的判别结果中挑选最终判别结果。

  

  根据少数服从多数的投票法能够得出，某条新数据最终应该属于类别1。

• “一对多”(One vs Rest, OvR)

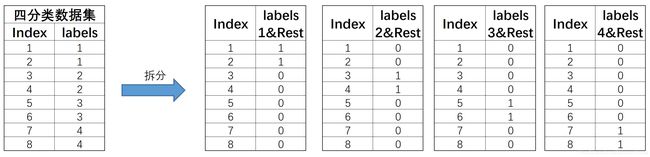
  和OvO的两两组合不同，OvR策略则是每次将一类的样例作为正例、其他所有数据作为反例来进行数据集拆分。对于上述四分类数据集，OvR策略最终会将其拆分为4个数据集，基本拆分过程如下

对于集成策略，它和划分策略息息相关，对于OvR方法来说，对于新数据的预测，如果仅有一个分类器将其预测为正例，则新数据集属于该类。若有多个分类器将其预测为正例，则根据分类器本身准确率来进行判断，选取准确率更高的那个分类器的判别结果作为新数据的预测结果。

OvO和OvR的比较：

对于这两种策略来说，尽管OvO需要训练更多的基础分类器，但由于OvO中的每个切分出来的数据集都更小，因此基础分类器训练时间也将更短。综合来看在训练时间开销上，OvO往往要小于OvR。而在性能方面，大多数情况下二者性能类似。

• “多对多”(Rest vs Rest, RvR)

  相比于OvO和OvR，MvM是一种更加复杂的策略。

  MvM要求同时将若干类化为正类、其他类化为负类，并且要求多次划分，再进行集成。

  通常会采用一种名为“纠错输入码”（Error Correcting Output Codes，简称ECOC）的技术来实现MvM过程。

  此时对于上述4分类数据集，拆分过程就会变得更加复杂。我们可以任选其中一类作为正类、其余作为负类，也可以任选其中两类作为正类、其余作为负数，以此类推。由此则诞生出了非常多种子数据集，对应也将训练非常多个基础分类器。

根据上述划分方式，总共将划分$C_4^1+C_4^2=10$
个数据集.对应的我们可以构建10个分类器。不过一般来说对于ECOC来说我们不会如此详尽的对数据集进行划分，而是再上述划分结果中挑选部分数据集进行建模，例如就挑选上面显式表示的4个数据集来进行建模，即可构建4个分类器。

不难看出，OvR实际上是MvM的一种特例

接下来进行模型集成。值得注意的是，如果是以上述方式划分四个数据集，我们可以将每次划分过程中正例或负例的标签所组成的数组视为每一条数据自己的编码。如下所示：

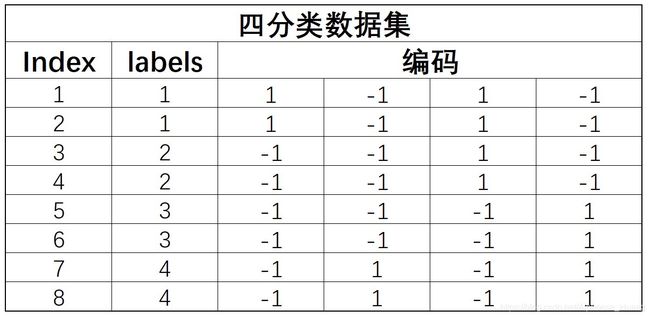
同时，使用训练好的四个基础分类器对新数据进行预测，也将产生四个结果，而这四个结果也可构成一个四位的新数据的编码。

接下来，我们可以计算新数据的编码和上述不同类别编码之间的距离，从而判断新生成数据应该属于哪一类。

我们可以以看到，如果预测足够准确，编码其实是和类别一一对应的。但如果基础分类器预测类别不够准确，编码和类别并不一定会一一对应，有一种三元编码方式，会将这种情况的某个具体编码改为0（纠错输出码），意为停用类。

对于计算距离的方法其实有很多种，常见的有欧式距离、街道距离以及闵可夫斯基距离。

• ECOC方法评估

  对于ECOC方法来说，编码越长预测结果越准确，不过编码越长也代表着需要耗费更多的计算资源，并且由于模型本身类别有限，因此数据集划分数量有限，编码长度也会有限。不过一般来说，相比OvR，MvM方法效果会更好。

5.逻辑回归的损失函数

一般来说，逻辑回归的损失函数的构建主要有两种方法。分别为通过极大似然估计和通过相对熵构建交叉熵损失函数。

构建损失函数的基本思路

Length	Species
1	0
3	1

由于只有一个特征Length，因此构建逻辑回归模型为:
$$y=sigmoid(\omega x+b)=\frac{1}{1+e^{-(\omega x+b)}}$$

在此，将模型输出结果看作概率，则代入数据可得模型结果
$$\begin{array}{rl}& p(y=1|x=1)=\frac{1}{1+e^{-(\omega +b)}}\\ & p(y=1|x=3)=\frac{1}{1+e^{-(3\omega +b)}}\end{array}$$

其中$p(y=1|x=1)$表示 $x$ 取值为1时 $y$ 取值为1的条件概率。而我们知道，两条数据的真实情况为第一条数据 $y$ 取值为0，而第二条数据 $y$ 取值为1，因此我们可以计算$p(y=0|x=1)$如下:

$$p(y=0|x=1)=1-p(y=1|x=1)=1-\frac{1}{1+e^{-(\omega +b)}}=\frac{e^{-(\omega +b)}}{1+e^{-(\omega +b)}}$$

可得:

Length	Species	1-predict	0-predict
1	1	$\frac{1}{1+e^{-(\omega +b)}}$	$\frac{e^{-(\omega +b)}}{1+e^{-(\omega +b)}}$
3	0	$\frac{1}{1+e^{-(3\omega +b)}}$	$\frac{e^{-(3\omega +b)}}{1+e^{-(3\omega +b)}}$

一般来说，损失函数的构建目标和模型评估指标保持一致（例如SSELoss和SSE）。对于大多数分类模型来说，模型预测的准确率都是最基础的评估指标。此处如果我们希望模型预测结果尽可能准确，就等价于希望$p(y=0|x=1)$和$p(y=1|x=1)$概率结果越大越好。该目标可以统一在求下式最大值的过程中：

$$p(y=0|x=1)\cdot p(y=1|x=3)$$

此外，考虑到损失函数一般都是求最小值，因此可将上式求最大值转化为对应负数结果求最小值，同时累乘也可以转化为对数相加结果，因此上式求最大值可等价于下式求最小值：

$$\begin{array}{rl}Loss& =-\ln (p(y=0|x=1))-\ln (p(y=1|x=3))\\ & =\ln (1+e^{-(3\omega +b)}+e^{\omega +b}+e^{-2\omega })\end{array}$$

至此构建了一个由两条数据所构成的逻辑回归损失函数.

为什么不用SSE计算

SSE运算如下：
$$||y-yha{t}_2^2|{|}_2^2=||y-\frac{1}{1+e^{-({\omega }^T\cdot x)}}|{|}_2^2$$
不用此方法的关键在于，在数学层面上我们可以证明，对于逻辑回归，当y属于0-1分类变量时，$||y-yha{t}_2^2|{|}_2^2$损失函数并不是凸函数，而非凸的损失函数将对后续参数最优解求解造成很大麻烦。而相比之下，概率连乘所构建的损失函数是凸函数，可以快速求解出全域最小值。

为什么将上述累计函数从累乘变为对数累加

原因在于，在实际建模运算过程中，尤其是面对大量数据进行损失函数构建过程中，由于有多少条数据就要进行多少次累乘，而累乘的因子又是介于(0,1)之间的数，因此极有可能累乘得到一个非常小的数。而通用的计算框架***计算精度***有限，即有可能在累乘的过程中损失大量精度，而转化为对数累加之后能够很好的避免该问题的发生。

求解损失函数

从数学角度可以证明，按照上述构成构建的逻辑回归损失函数仍然是凸函数，此时我们仍然可以通过对$LogitLoss(\omega ,b)$求偏导然后令偏导函数等于0、再联立方程组的方式来对参数进行求解。

$$\begin{array}{rl}& \frac{\partial LogitLoss(\omega ,b)}{\partial \omega }=0\\ & \frac{\partial LogitLoss(\omega ,b)}{\partial \omega }=0\end{array}$$

6.使用极大似然估计求解损失函数

极大似然估计知识点

逻辑回归模型:
$$y=\frac{1}{1+e^{-({\omega }^T\cdot x)}}$$

其中：
$$\omega =[{\omega }_1,{\omega }_2,...,{\omega }_n,b{]}^T,x=[x_1,x_2,...,x_n,b{]}^T$$

求解过程总共分为以下四个步骤：

• 确定似然项

  我们知道，对于逻辑回归来说，当$\omega$和$x$取得一组之后，既可以有一个概率预测输出结果，即：

  $$p(y=1|x;\omega )=\frac{1}{1+e^{-({\omega }^T\cdot x)}}$$

  而对应取0的概率为：
  $$1-p(y=1|x;\omega )=1-\frac{1}{1+e^{-({\omega }^T\cdot x)}}$$

  可以令

  $$\begin{array}{rl}& p_1(x,\omega )=p(y=1|x;\omega )\\ & p_0(x,\omega )=1-p(y=1|x;\omega )\end{array}$$

  因此，第$i$个数据所对应的似然项可以写成：
  $$p_1(x,\omega {)}^{y_i},p_0(x,\omega {)}^{1-y_i}$$
  其中，$y_i$表示第$i$条数据对应的类别标签。不难发现，当$y_i=0$时，代表的是$i$第条数据标签为0，此时需要带入似然函数的似然项是$p_0(x,\omega )$。反之，当$y_i=1$时，代表的是$i$第条数据标签为1，此时需要带入似然函数的似然项是$p_1(x,\omega )$。上述似然项可以同时满足这两种不同的情况。

• 似然函数的构建

  通过似然项的累乘计算极大似然函数：
  $$\prod _{i=1}^N[p_1(x;\omega {)}^{y_i}\cdot p_0(x;\omega {)}^{1-y_i}]$$

• 对数转换

  $$\begin{array}{rl}L(\omega )& =-\ln (\prod _{i=1}^N[p_1(x;\omega {)}^{y_i}\cdot p_0(x;\omega {)}^{1-y_i}])\\ & =\sum _{i=1}^N[-y_i\cdot \ln (p_1(x;\omega ))-(1-y_i)\cdot \ln (1-p_1(x;\omega ))]\end{array}$$

  后续我们将借助该公式进行损失函数求解。

• 对数似然函数的求解

  通过一系列数学过程可以证明，通过极大似然估计构建的损失函数是凸函数，此时我们可以采用导数为0联立方程组的方式进行求解。

  但这种方法会涉及大量的导数运算、方程组求解等，并不适用于大规模甚至是超大规模数值运算。因此，在机器学习领域，通常会采用一些更加通用的优化方法对逻辑回归的损失函数进行求解，通常来说是牛顿法或者梯度下降算法。

7. 通过相对熵构建交叉熵损失函数

通过相对熵构建交叉熵损失函数