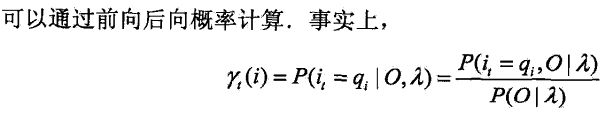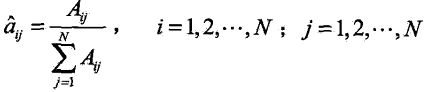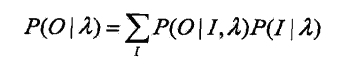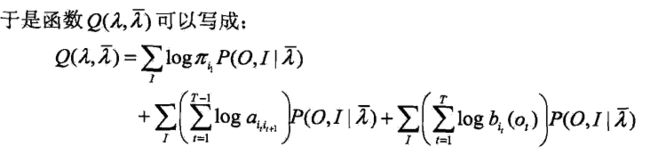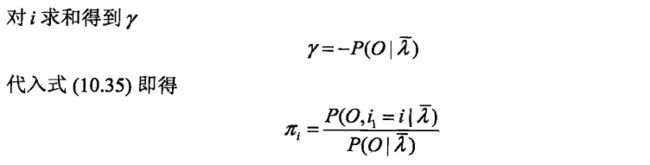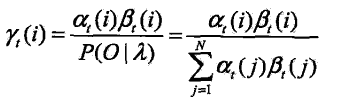转自:小象学院+自己总结
模型+策略+算法
隐马尔可夫模型是用于标注问题,描述由隐藏的马尔科夫链随机生成观测序列的过程,属于生成模型。在语音识别、自然语言处理、生物信息、模式识别等领域有广泛应用。
是关于时序的概率模型,描述隐变量的随机状态,以及隐藏状态生成观测序列。每个观测序列又可以看作是一个时刻。
模型由初始概率分布、状态转移概率分布以及观测概率分布确定。Q为所有可能状态的集合,V是所有可能观测的序列。
I是长度为T的状态序列,O为其对应的观测序列。
模型可以表示为:
其中包含两个假设:
1)齐次马尔科夫性假设,任意时刻t的状态只依赖于其前一时刻的状态,与其他时刻的状态和观测无关,也与时刻t无关
2)观测独立性假设,任意时刻的观测只依赖于该时刻的隐马尔可夫链的状态,与其他观测和状态无关。
三个基本问题:
1)概率计算问题:给定模型和观测序列,计算在模型lambda下观测序列O出现的概率P(O|lambda)
2)学习问题:已知观测序列O,估计模型lambda的参数,使得P(O|lambda)最大,用极大似然估计的方法来估计参数
3)预测问题:也称为解码,已知模型lambda和观测序列O求P(I|O)最大的I,即最有可能的状态序列。
后续进行中文分词实践
问题1:概率计算算法,计算观测序列概率P(O|lambda)前向和后向算法
首先先介绍一下直接计算。
最直接的方法是通过列举所有可能长度为T的状态序列,求各个状态序列I与观测序列O的联合概率P(O,I|lambda),然后对所有状态序列求和得到P(O|lambda)
可以看出计算量非常大,是O(TN^T)阶的,因此不可行,需要引入前向后向算法
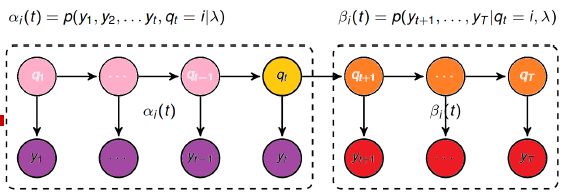
前向概率:
步骤1初始化前向概率,是初始时刻状态i1=qi和观测o1的联合概率
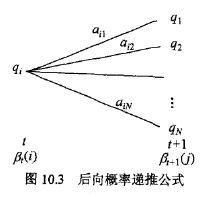
步骤2是前向概率的递推公式,计算时刻r+1部分的观测序列为o1,o2,...,ot,ot+1,且在时刻t+1处于状态qi的前向概率。对于这个乘积在时刻t的所有可能的N个状态qj求和,其结果就是得到在时刻t+1达到状态qi的联合概率
可以看出前向算法实际是基于状态序列的路径结构递推计算,高效的关键在于局部计算前向概率。
这样时间复杂度就降为了O(N^2T)
后向算法:
注意:前向概率计算出的是P(O,I|lambda),因此只需把所有状态的概率相加即可
后向概率计算的是P(O|I,lambda),意思就是最后一个状态已经知道了,那么P(O,I|lambda)=P(O|I,lambda)*P(O|I)再把所有状态加起来
监督学习(极大似然估计)和非监督学习BW算法(EM)
监督学习:
1. 转移概率aij的估计
设样本中时刻t处于状态i时刻t+1转移到状态j的频数为Aij那么aij的估计是
2. 观测概率bj(k)的估计
设样本中状态为j并观测为k的频数是Bij,那么状态为j观测为k的概率bj(k)的估计是
3. 初始状态概率pi的估计为初始状态为qi的频数
由于监督学习需要使用训练数据,而人工标注数据的代价很高,所以我们常用非监督学习的方法
非监督学习Baum-welch算法
隐马尔可夫模型可以看作下面这个模型
它的参数学习可以由EM算法实现
1. 确定完全数据的对数似然函数logP(O,I | lambda)
2. EM算法的E步:求Q函数Q(lambda,lambda^)
3. EM算法的M步:极大化Q函数,求模型中的A,B,PI
由于要极大化Q函数里的三项,可以对其进行分别极大化
第二项式子可以写成
第三项可以写为:
问题3:解码问题
可以用近似算法或者是维特比算法(viterbi)
近似算法:在每个时刻t选择在该时刻最可能出现的状态it。推广到一个状态序列
近似算法的优点是计算简单,其缺点是不能保证预测状态序列是整体最优序列,因为从整体的角度有可能不发生,存在转移概率为0的情况
维特比算法:实际是用动态规划求解隐马尔可夫模型预测问题,即用动态规划求得概率最大路径(最优路径)
根据动态规划原理,最优路径具有这样的特性:如果最优路径在时刻t通过节点it,那么这条路径从节点it到终点iT部分的路径是最优的。
因此我们只需要从t=1开始,递推地计算在时刻t状态为i的各条部分路径的最大概率,直到t=T
注意前向概率和后项概率之间的关系
当状态为离散,观测值为连续时,要使用高斯隐马尔可夫