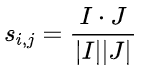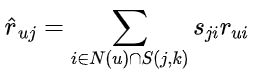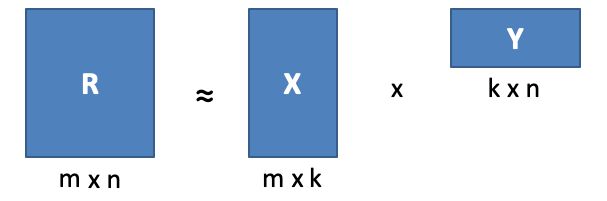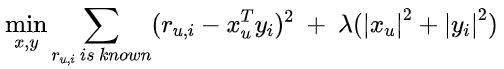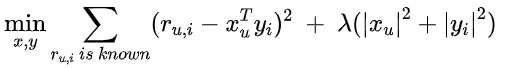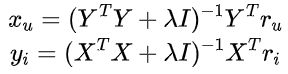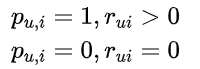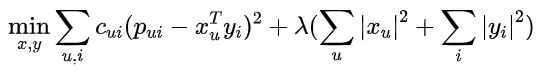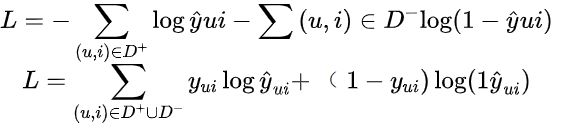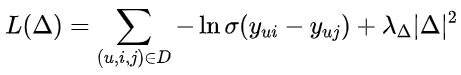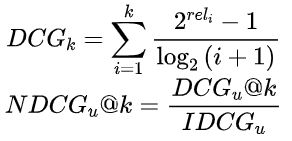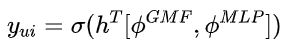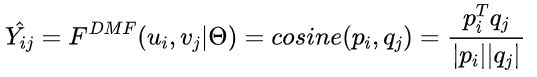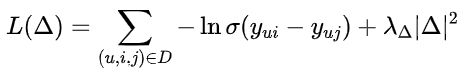案例分享 | 深度学习在花椒直播中的应用 — 神经网络与协同过滤篇
案例来源于花椒直播 ,作者花椒智能工程
一、协同过滤算法概述
协同过滤 (Collaborative Filtering) 算法一经发明便在推荐系统中取得了非凡的成果。许多知名的系统早期都采用了协同过滤算法,例如 Google News,亚马逊、Hulu、Netflix 等。
协同过滤算法一般采用评分矩阵来表示用户和物品的交互,评分矩阵 ![]() 中的每一个元素
中的每一个元素 ![]() 表示用户
表示用户 ![]() 对物品
对物品 ![]() 的喜好评分。由于用户不能对大部分物品都有交互,所以在很多场景下评分矩阵都很稀疏,稀疏率在 90% 以上,稀疏度很高决定算法在优化和选取上有很多考量。
的喜好评分。由于用户不能对大部分物品都有交互,所以在很多场景下评分矩阵都很稀疏,稀疏率在 90% 以上,稀疏度很高决定算法在优化和选取上有很多考量。
传统协同过滤算法
传统的协同过滤分为 user base 和 item base 两种算法,这两种算法的核心思想是一样的,我们以 item base 算法为例,说明算法的具体流程:
1. 计算物品之间的相似度,我们利用评分矩阵的列向量作为每一个物品 ![]() 的向量,然后运用余弦相似度来计算每两个物品之间的相似度
的向量,然后运用余弦相似度来计算每两个物品之间的相似度
2. 通过用户喜欢的物品集合,计算出用户 ![]() 对物品
对物品 ![]() 的分数
的分数
-
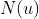 是用户
是用户  喜欢的物品集合
喜欢的物品集合 -
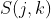 是和物品
是和物品  最相似的
最相似的  个物品的集合
个物品的集合 -
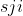 是物品
是物品  和
和  的相似度
的相似度 -
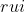 代表用户
代表用户  对物品
对物品  的分数
的分数
3. 通过上述计算的分数,从大到小召回 TopK 个物品
基于隐向量的协同过滤
传统的基于物品或用户的协同过滤有如下缺陷:
-
它们是一种基于统计的方法,而不是优化学习的方法,没有学习过程和设立指标进行优化得到最优模型的过程
-
没有用到全局数据,只用了局部数据计算相似度、进行推荐
-
当用户或物品维度很大时,会占用很大的内存
基于以上缺陷,学者们又提出了广义的协同过滤算法,即基于基于隐向量的协同过滤。基于隐向量的协同过滤最早是隐语义模型 (LFM)。他的核心思想很朴素,利用矩阵分解,把很大很稀疏的评分矩阵 ![]() 分解成两个较为稠密的矩阵:
分解成两个较为稠密的矩阵:
它的优化目标一般使用 MSE 作为损失函数:
其中 ![]() 就是用户
就是用户 ![]() 的隐向量,
的隐向量,![]() 是物品
是物品 ![]() 的隐向量。
的隐向量。
目前推荐系统中应用的协同过滤算法一般都是基于隐向量的协同过滤算法。登录 B 站 Google 中国 TensorFlow 频道观看《使用 TensorFlow 搭建推荐系统系列(全八讲)》视频,可了解更多关于过滤与协同过滤的内容。
显式反馈和隐式反馈
显示反馈是用户直接对物品进行喜好打分,比如豆瓣电影,IMDB 电影打分。隐式反馈主要出现在互联网应用场景,一般很难收集到用户对物品的直接喜好打分,转而寻求隐含的偏好倾向,例如点击次数、点赞、观看时长等
| 显式反馈 | 隐式反馈 |
|---|---|
| 用户主动表示对物品的喜好分数,例如豆瓣电影打分,IMDB 电影打分 | 用户对物品的行为交互频率,比如说观看次数,点赞次数,观看时长…… |
| 分数代表喜欢程度 | 数值只是代表交互程度,并不能明确表示喜欢程度 |
| 适用于有收集喜好打分的网站,应用面比较狭窄 | 适用于目前互联网大部分应用场景 |
花椒中用到的矩阵分解算法也是基于隐式反馈,本文接下来篇幅中介绍的神经网络协同过滤算法也都是基于隐式反馈。需要注意的是,基于隐式反馈的算法,都会引入负反馈来训练,由于负反馈的量级远远大于正反馈,负反馈一般采用随机采样的方法,一个正样本搭配 5 个负样本。
在基于隐式反馈的协同过滤算法中, Spark 上实现了 ALS 算法,Spark 上实现的接口简单易用,计算迅速,部署简答,目前很多应用都基于 ALS 算法进行快速搭建。ALS 算法的应用实例如下:
from pyspark.mllib.recommendation import ALS, MatrixFactorizationModel, Rating
# Load and parse the data
data = sc.textFile("data/mllib/als/test.data")
ratings = data.map(lambda l: l.split(','))\
.map(lambda l: Rating(int(l[0]), int(l[1]), float(l[2])))
# Build the recommendation model using Alternating Least Squares
rank = 10
numIterations = 10
model = ALS.trainImplicit(ratings, rank, numIterations, alpha=10)
# Evaluate the model on training data
testdata = ratings.map(lambda p: (p[0], p[1]))
predictions = model.predictAll(testdata).map(lambda r: ((r[0], r[1]), r[2]))
ratesAndPreds = ratings.map(lambda r: ((r[0], r[1]), r[2])).join(predictions)
MSE = ratesAndPreds.map(lambda r: (r[1][0] - r[1][1])**2).mean()
print("Mean Squared Error = " + str(MSE))二、损失函数的选择
基于回归的损失函数
基于显式反馈的矩阵分解算法,采用 MSE 作为损失函数,他拟合稀疏矩阵中所有有值的元素。他的计算公式如下:
它的求解方法一般采用交替最小二乘法,交替固定 ![]() ,不断迭代求解
,不断迭代求解
隐式反馈的损失函数,设置稍微复杂,需要考虑隐式反馈强度的设定,步骤如下:
-
首先定义用户对物品的偏好
-
其次定义用户
 对物品
对物品  偏好置信度,反馈次数越多,越确信用户对物品的偏好
偏好置信度,反馈次数越多,越确信用户对物品的偏好
-
定义损失函数为
-
用 ALS 算法求解
交叉熵损失函数
这类方法把隐式反馈划归为分类问题,有反馈的用户物品 pair 类别是 1,没有反馈的用户物品 pair 类别是 0,这样就可以用交叉熵损失函数来求解二分类问题。交叉熵损失函数定义如下:
交叉熵损失函数一般用随机梯度下降 (SGD) 算法来求解。
BPR 损失函数
传统的矩阵分解是一种 point-wise 算法,很多实验表明, 并不是错误率越低最终的推荐表现就越好,它可能的原因有:
-
衡量错误率和排序表现的指标之间存在差异
-
观测到的数据和实际情况有偏差,即用户更加倾向于给喜欢的物品打分
BPR 是 pair-wise 排序算法中的一种,他的核心思想是对用户每一个正反馈,都随机采样 n 个负反馈,并且最大化他们的分数差距,它优化的是两个物品间的相对排序,而不是单个物品的绝对分数。BPR 损失函数定义如下:
BPR 损失函数一般用随机梯度下降 (SGD) 算法来求解。
三、神经网络与协同过滤
负采样
目前基于深度学习的协同过滤算法一般都采用隐式反馈数据,这些算法都需要对已经观测到的正反馈数据,采样负反馈数据,对于交叉熵损失函数,采样的负反馈数据直接标记成类别 0,对于 BPR 损失函数,负采样的数据则被放到损失函数 ![]() 偏置对中的
偏置对中的 ![]() 部分负采样一般采取随机采样,对一个正样本随机采样
部分负采样一般采取随机采样,对一个正样本随机采样 ![]() 个负样本,
个负样本,![]() 的设置值得考量。
的设置值得考量。![]() 设置过小,每个 epoch 训练不够充分,
设置过小,每个 epoch 训练不够充分,![]() 设置过大,有过拟合的风险,同时会增加模型的数据量,影响训练速度。经过花椒的实践,
设置过大,有过拟合的风险,同时会增加模型的数据量,影响训练速度。经过花椒的实践,![]() 设置为 5 比较恰当。
设置为 5 比较恰当。
优化器的选择
我们模型一般采用交叉熵和 BPR 损失函数,所以采用 SGD 类的方法作为优化器,经过我们的训练和使用,Adam 方法得益于自适应学习率和动量学习,在收敛速度和模型效果上能到到较好的平衡,所以我们模型采用 Adam 作为优化器。
离线评估方法
传统矩阵分解采用 MSE 作为评估方法不太恰当,只考虑了测试机上的整体误差,没有考虑每个人推荐列表的相对顺序,这种评估方法和实际推荐系统中用户的点击行为不匹配,离线评估效果不能作为线上效果的依据。
我们采用 ndcg 和 hit ratio 作为我们离线评估指标, ndcg 侧重于考量推荐列表中位置关系,hr 则侧重评估在 topk 问题中的命中率。其中ndcg的定义如下:
评估方法,我们采取的是 leave one out 方法,它的详细步骤如下:
-
对每个用户,选取最近的一条正反馈样本当测试样本
-
对测试机中每个正样本,随机采样 100 个没有交互的负样本
-
对每个用户的 101 个样本,输入到模型获取评估分数
-
对每个用户的 101 个样本,按照堆排序方法,获取 top k 个样本,评估 ndcg 和 hr 分数
-
求出整个测试集的整体 ndcg 和 hr
评估方法的 tensorflow 代码如下所示:
def evaluate(user_data, sess, model):
ndcg = 0.0
hr = 0.0
for u in user_data:
to_test = user_data[u]['scores']
true_id = user_data[u]['true_id']
uid, mid, y = zip(*to_test)
feed_dic = {
model['uid']: uid,
model['i']: mid,
model['keep_probe']: 1.0
}
score, user_emb = sess.run([model['score'], model['user_vec']], feed_dict=feed_dic)
predict = []
# print("user+++++ uid=%d, trueid=%d, loss=%.5f" % (u, true_id, loss))
for i, row in enumerate(to_test):
predict.append((row[0], row[1], score[i]))
ranklist = heapq.nlargest(TOP_K, predict, key=lambda r: r[2])
u_ndcg = 0.0
u_hr = 0.0
for i, row in enumerate(ranklist):
if row[1] == true_id:
u_ndcg = 1 / math.log2(2 + i)
u_hr += 1
ndcg += u_ndcg
hr += u_hr
if u == 6040:
print(user_emb[0])
print(u, ranklist)
print("~~~~~~uid=%d, u_ndcg=%.5f" % (u, u_ndcg))
ndcg = ndcg / len(user_data)
hr = hr / len(user_data)
time = datetime.datetime.now().isoformat()
print("%s ------------------- evaluate ndcg(10)=%.5f, hr(10)=%.5f" % (time, ndcg, hr))
四、花椒推荐系统发展史
在接下来篇幅中,我们将着重介绍一些花椒推荐系统在实际中尝试过的基于神经网络的协同过滤模型。
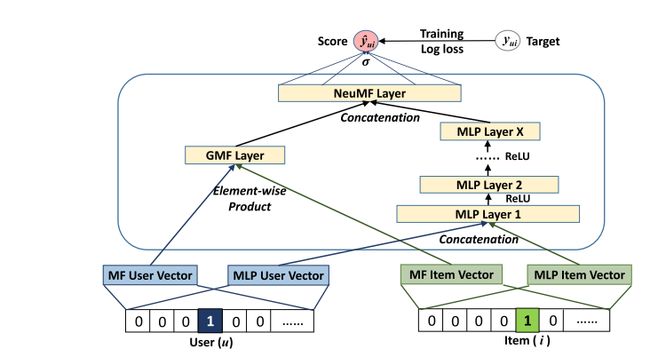
通用矩阵分解模型(GMF)
这个是何向南提出的 NCF 算法中的一部分,他提出了一种通过的矩阵分解模型,模型构建步骤如下
-
用户隐向量和物品隐向量按位相乘, 其中 ⊙ 符号代表向量按位相乘
-
计算用户 u 和 物品 i 之间的分数, 其中 就是我们要拟合的最后一层参数
-
采用 sigmod 函数当做最后一层的激活函数,将 输入到交叉熵损失函数中训练
GMF 模型中如果 ![]() 全是1,那么他就会退化为普通的矩阵分解中的点积。模型实例代码如下
全是1,那么他就会退化为普通的矩阵分解中的点积。模型实例代码如下
def model_fn():
uid = tf.placeholder(tf.int32, shape=[None])
item = tf.placeholder(tf.int32, shape=[None])
y = tf.placeholder(tf.float32, shape=[None])
user_emb = tf.Variable(initial_value=tf.truncated_normal(shape=[USER_COUNT + 1, EMB_SIZE], mean=0, stddev=0.5),
name="user_emb")
movie_emb = tf.Variable(initial_value=tf.truncated_normal(shape=[MOVIE_COUNT + 1, EMB_SIZE], mean=0, stddev=0.5),
name="movie_emb")
user_vec = tf.nn.embedding_lookup(user_emb, uid)
item_vec = tf.nn.embedding_lookup(movie_emb, item)
layer = tf.multiply(user_vec, item_vec)
last_layer = tf.keras.layers.Dense(1, None,
kernel_initializer=tf.random_normal_initializer(stddev=0.5),
kernel_regularizer=tf.keras.regularizers.l2(L2_LAMBDA),
bias_initializer=tf.random_normal_initializer(stddev=0.5),
bias_regularizer=tf.keras.regularizers.l2(L2_LAMBDA))
logits = last_layer.apply(layer)
logits = tf.reshape(logits, (-1,))
l2_loss = tf.losses.get_regularization_loss()
score = tf.sigmoid(logits)
label = tf.minimum(y, 1.0)
loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(labels=label, logits=logits)) + l2_loss
return {"score": score,
"loss": loss,
'uid': uid,
"i": item,
"y": y,
}
MLP 模型
相对于 GMF 拟合用户向量和物品向量的线性关系,MLP 模型期望用多层神经网络拟合用户向量和物品向量之间的高阶非线性关系,同 GMF 模型一样,MLP 模型也采用交叉熵作为损失函数,它的构建步骤如下:
-
将用户向量和物品向量 concat 起来
-
concat 后的向量输入到 MLP 模型中
-
MLP 最后一层用 sigmod 函数激活输入到交叉熵损失函数
-
梯度下降求解模型参数
MLP 模型的示例代码如下
def model_fn():
uid = tf.placeholder(tf.int32, shape=[None])
item = tf.placeholder(tf.int32, shape=[None])
y = tf.placeholder(tf.float32, shape=[None])
keep_prob = tf.placeholder(tf.float32)
user_emb = tf.Variable(initial_value=tf.truncated_normal(shape=[USER_COUNT + 1, EMB_SIZE], mean=0, stddev=0.01))
movie_emb = tf.Variable(initial_value=tf.truncated_normal(shape=[MOVIE_COUNT + 1, EMB_SIZE], mean=0, stddev=0.01))
user_vec = tf.nn.embedding_lookup(user_emb, uid)
item_vec = tf.nn.embedding_lookup(movie_emb, item)
# input = tf.multiply(user_vec, item_vec)
input = tf.concat([user_vec, item_vec], axis=1)
output_size = EMB_SIZE * 2
layers = []
for i in range(2):
output_size = output_size / 2
l = tf.keras.layers.Dense(output_size,
activation=tf.nn.relu,
kernel_initializer=tf.truncated_normal_initializer(stddev=0.1),
kernel_regularizer=tf.keras.regularizers.l2(L2_RATE),
bias_regularizer=tf.keras.regularizers.l2(L2_RATE),
)
layers.append(l)
for l in layers:
input = l(input)
input = tf.nn.dropout(input, keep_prob=keep_prob)
last_layer = tf.keras.layers.Dense(1, activation=None,
kernel_initializer=tf.truncated_normal_initializer(stddev=0.1),
kernel_regularizer=tf.keras.regularizers.l2(L2_RATE),
bias_regularizer=tf.keras.regularizers.l2(L2_RATE))
logits = last_layer(input)
logits = tf.reshape(logits, (-1,))
score = tf.sigmoid(logits)
l2_loss = tf.losses.get_regularization_loss()
loss = l2_loss + tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(labels=y, logits=logits))
return {"score": score,
"loss": loss,
'uid': uid,
"item": item,
'y': y,
}
NeuMF 模型
GMF 和 MLP 模型分别能拟合用户、物品向量的线性和非线性关系,联想自 Google 提出的 Wide and Deep Recommendation 算法,我们也自然而然的将 GMF 和 MLP 算法融合起来,期望能拟合更为复杂用户、物品交互关系。NeuMF 模型的构建步骤为:
-
预训练 GMF 和 MLP 模型的隐向量和MLP部分参数
-
将 GMF 和 MLP 最后一层融合到一起输入到损失函数
-
梯度下降方法更新每一层参数
NeuMF 模型的结构为:
NeuMF 模型的示例代码为:
def model_fn():
uid = tf.placeholder(tf.int32, shape=[None])
item = tf.placeholder(tf.int32, shape=[None])
y = tf.placeholder(tf.float32, shape=[None])
dropout_rate = tf.placeholder(tf.float32)
mf_user_emb = tf.get_variable(name='mf_user_emb',
initializer=tf.truncated_normal_initializer(mean=0, stddev=0.1),
shape=[USER_COUNT + 1, MF_EMB_SIZE],
trainable=True,
regularizer=None
)
mf_movie_emb = tf.get_variable(name='mf_movie_emb',
initializer=tf.truncated_normal_initializer(mean=0, stddev=0.1),
shape=[MOVIE_COUNT + 1, MF_EMB_SIZE],
trainable=True,
regularizer=None
)
mlp_user_emb = tf.get_variable(name='mlp_user_emb',
initializer=tf.truncated_normal_initializer(mean=0, stddev=0.1),
shape=[USER_COUNT + 1, MLP_EMB_SIZE],
trainable=True,
regularizer=None
)
mlp_movie_emb = tf.get_variable(name='mlp_movie_emb',
initializer=tf.truncated_normal_initializer(mean=0, stddev=0.1),
shape=[MOVIE_COUNT + 1, MLP_EMB_SIZE],
trainable=True,
regularizer=None)
user_mf_vec = tf.nn.embedding_lookup(mf_user_emb, uid)
item_mf_vec = tf.nn.embedding_lookup(mf_movie_emb, item)
mf_layer = tf.multiply(user_mf_vec, item_mf_vec)
mlp_user_vec = tf.nn.embedding_lookup(mlp_user_emb, uid)
mlp_movie_vec = tf.nn.embedding_lookup(mlp_movie_emb, item)
input = tf.concat([mlp_user_vec, mlp_movie_vec], axis=1)
#input = tf.multiply(mlp_user_vec, mlp_movie_vec)
layers = []
size = MLP_EMB_SIZE
for i in range(2):
l = tf.keras.layers.Dense(size,
activation=tf.nn.relu,
bias_regularizer=tf.keras.regularizers.l2(L2_LAMBDA),
kernel_regularizer=tf.keras.regularizers.l2(L2_LAMBDA),
kernel_initializer=tf.contrib.layers.xavier_initializer())
layers.append(l)
input = l.apply(input)
input = tf.nn.dropout(input, keep_prob=1 - dropout_rate)
size = size / 2
layer = tf.concat([mf_layer, input], axis=1)
last_layer = tf.layers.Dense(1,
activation=None,
kernel_regularizer=tf.keras.regularizers.l2(L2_LAMBDA),
kernel_initializer=tf.contrib.layers.xavier_initializer(),
bias_regularizer=tf.keras.regularizers.l2(L2_LAMBDA)
)
logits = last_layer.apply(layer)
logits = tf.reshape(logits, shape=(-1,))
l2_loss = tf.losses.get_regularization_loss()
score = tf.sigmoid(logits)
loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(labels=y, logits=logits)) + l2_loss
return {"score": score,
"loss": loss,
'uid': uid,
"i": item,
"y": y,
"dropout_rate": dropout_rate,
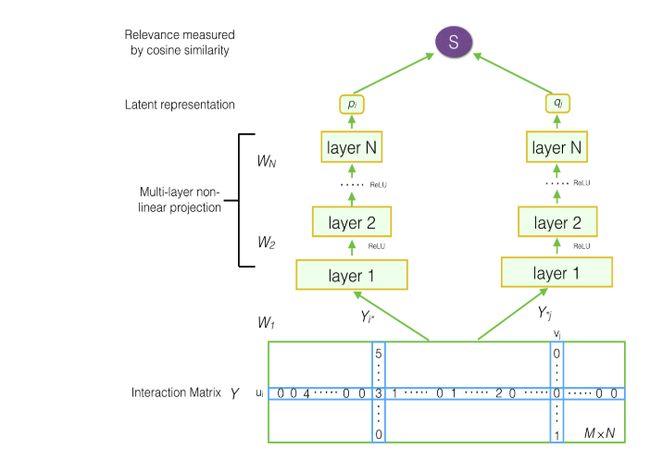
}深度矩阵分解模型 (DMF)
模型结构
深度矩阵分解模型,跟上面的 NeuMF 不同之处在于,它不采用 embedding 向量作为模型的输入,转而直接采用评分矩阵 ![]() 中的行、列原始数据作为模型的输入。在评分矩阵
中的行、列原始数据作为模型的输入。在评分矩阵 ![]() 中,每个用户
中,每个用户 ![]() 都被表示为一个高维向量
都被表示为一个高维向量 ![]() , 它表示的是第
, 它表示的是第 ![]() 个用户对所有物品的频分。同样的,每个物品
个用户对所有物品的频分。同样的,每个物品 ![]() 都被表示成一个高维向量
都被表示成一个高维向量 ![]() , 它表示的是所有用户对第
, 它表示的是所有用户对第 ![]() 个物品的评分。该模型的构建步骤如下:
个物品的评分。该模型的构建步骤如下:
-
对所有的用户、物品获取高维的表示向量
-
将用户、物品的高维向量分别输入到两个 MLP 网络
-
经过 MLP 处理后,用户和物品的向量分别变成了稠密向量
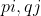
-
用余弦相似度计算,用户对物品的评分
-
用梯度下降求解模型参数
DMF 模型的结构如下:
损失函数
DMF 模型采用的是交叉熵损失函数,即建模为一个二分类问题。DMF 模型的创新性在于,它注意到了公共数据集 movielens 中存在分数导致样本权重不一样的问题,一个评 1 分的电影和评 5 分的电影在损失函数中贡献的权重是一样的,这样有些违背常识,评分高的样本应该比评分低的样本设置更高的权重,因此 DMF 模型设置了一个归一化的交叉熵损失函数,定义如下:
![]()
可以看出正样本的权重会按照用户的分数的高低进行归一化。
模型示例代码
def model_fn(embs):
uid = tf.placeholder(tf.int32, shape=[None])
item = tf.placeholder(tf.int32, shape=[None])
y = tf.placeholder(tf.float32, shape=[None])
dropout_rate = tf.placeholder(tf.float32)
user_emb = tf.convert_to_tensor(embs)
movie_emb = tf.transpose(embs)
user_vec = tf.nn.embedding_lookup(user_emb, uid)
item_vec = tf.nn.embedding_lookup(movie_emb, item)
#
for i, u_size in enumerate(USER_LAYER):
i_size = ITEM_LAYER[i]
act = None
use_bias = False
if i > 0:
act = tf.keras.activations.relu
use_bias = True
l_u = tf.keras.layers.Dense(u_size,
activation=act,
use_bias=use_bias,
bias_regularizer=tf.keras.regularizers.l2(L2_LAMBDA),
kernel_regularizer=tf.keras.regularizers.l2(L2_LAMBDA),
kernel_initializer=tf.truncated_normal_initializer(stddev=0.01))
l_i = tf.keras.layers.Dense(i_size,
activation=act,
use_bias=use_bias,
bias_regularizer=tf.keras.regularizers.l2(L2_LAMBDA),
kernel_regularizer=tf.keras.regularizers.l2(L2_LAMBDA),
kernel_initializer=tf.truncated_normal_initializer(stddev=0.01))
user_vec = l_u.apply(user_vec)
item_vec = l_i.apply(item_vec)
dot = tf.reduce_sum(tf.multiply(user_vec, item_vec), axis=1)
mod_u = tf.sqrt(tf.reduce_sum(tf.square(user_vec), axis=1))
mod_i = tf.sqrt(tf.reduce_sum(tf.square(item_vec), axis=1))
y_ = dot / (mod_u * mod_i)
y_ = tf.maximum(MIU, y_)
score = y_
# loss = tf.reduce_sum(tf.where(tf.greater(y, 0), tf.log(y_), tf.log(1.0 - y_)))
norm_rate = y / 5.0
loss = tf.reduce_sum(norm_rate * tf.log(y_) + (1.0 - norm_rate) * tf.log(1.0 - y_))
l2_loss = 0.0# tf.losses.get_regularization_loss()
loss = l2_loss - loss
return {"score": score,
"loss": loss,
'uid': uid,
"i": item,
"y": y,
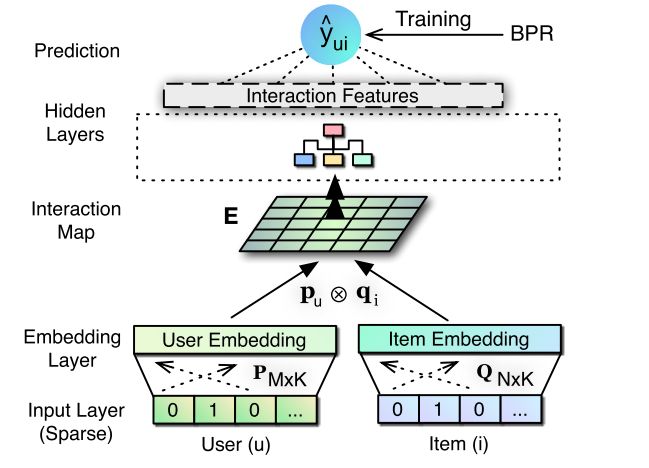
}基于卷积的矩阵分解模型(ConvMF)
模型结构
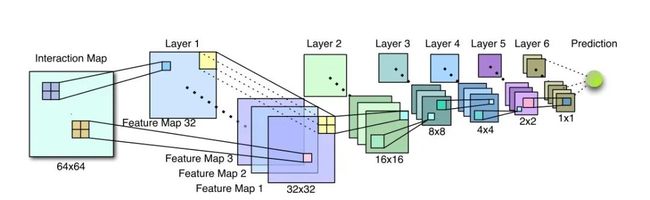
ConvMF 是目前的 state-of-the-art 模型,在公共数据集上表现的效果最好,主要原因是他通过卷积神经网络 (CNN) 充分挖掘出用户和物品之间的交互特征。他的创新点如下:
-
首次用外积 (Outer Product) 来表示用户和物品之间的交互信息
-
创新性的用 CNN 网络来挖掘用户和物品交互信息
ConvMF 模型简洁、清晰、明了,是深度学习中不可多见的精品模型,他的构建步骤如下:
-
用稠密的 embedding 表示用户和物品的隐向量分别为
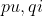 ,他们的维度为
,他们的维度为 
-
对用户和物品,计算他们的外积,形成
 ×
×  的矩阵
的矩阵  ,
,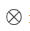 表示外积运算
表示外积运算
-
将交叉矩阵输入到二维的 CNN 网络得到一维向量
-
一维向量线性拟合出分数
-
计算损失函数,用梯度下降求解
模型结构如下:
CNN 网络结构如下
可以看到 CNN 结构同图像领域典型的卷积-池化的结构不太一样,每一层卷积都采用 strides 为 2 ,使得交叉矩阵的大小不断减半,直至最后一层演变成一维向量。
损失函数
ConvMF 的损失函数采用的是 BPR 损失函数
模型示例代码
模型结构部分:
def model_fn():
uid = tf.placeholder(tf.int32, shape=[None])
item_i = tf.placeholder(tf.int32, shape=[None])
item_j = tf.placeholder(tf.int32, shape=[None])
keep_prob = tf.placeholder(tf.float32)
user_emb = tf.Variable(initial_value=tf.truncated_normal(shape=[USER_COUNT + 1, EMB_SIZE], mean=0, stddev=0.01))
movie_emb = tf.Variable(initial_value=tf.truncated_normal(shape=[MOVIE_COUNT + 1, EMB_SIZE], mean=0, stddev=0.01))
user_vec = tf.nn.embedding_lookup(user_emb, uid)
i_vec = tf.nn.embedding_lookup(movie_emb, item_i)
j_vec = tf.nn.embedding_lookup(movie_emb, item_j)
w = tf.get_variable('w_',
shape=[FILTER_COUNT],
initializer=tf.truncated_normal_initializer(stddev=0.1),
regularizer=tf.keras.regularizers.l2(L2_W)
)
b = tf.get_variable('b_',
shape=[1],
initializer=tf.random_normal_initializer(stddev=0.1),
regularizer=tf.keras.regularizers.l2(L2_W)
)
conv_layers = []
for i in range(6):
conv_layers.append(tf.keras.layers.Conv2D(filters=FILTER_COUNT,
kernel_size=(2, 2),
strides=(2, 2),
padding='SAME',
activation=tf.nn.relu,
kernel_regularizer=tf.keras.regularizers.l2(L2_CONV),
bias_regularizer=tf.keras.regularizers.l2(L2_CONV)
)
)
x_i = conv(user_vec, i_vec, keep_prob, w, b, conv_layers)
x_j = conv(user_vec, j_vec, keep_prob, w, b, conv_layers)
l2_loss = tf.losses.get_regularization_loss() + L2_EMB * (l2(user_vec) + l2(i_vec) + l2(j_vec))
loss = l2_loss - tf.reduce_sum(tf.log(tf.sigmoid(x_i - x_j)))
return {"score": x_i,
"loss": loss,
'uid': uid,
"i": item_i,
"j": item_j,
"user_vec": user_vec,
}
卷积部分:
def conv(user_emb, item_emb, keep_prob, w, b, conv_layers):
user_emb_1 = tf.reshape(user_emb, shape=[-1, EMB_SIZE, 1])
item_emb_t = tf.reshape(item_emb, shape=[-1, 1, EMB_SIZE])
matrix = tf.matmul(user_emb_1, item_emb_t)
matrix = tf.expand_dims(matrix, -1)
input = matrix
for l in conv_layers:
input = l(input)
input = tf.nn.dropout(input, keep_prob=keep_prob)
print(input.shape)
layer = tf.nn.dropout(input, keep_prob=keep_prob)
layer = tf.reshape(layer, [-1, FILTER_COUNT])
y = tf.reduce_sum(tf.multiply(layer, w), axis=1) + b
return y
五、深度协同过滤模型在花椒的应用
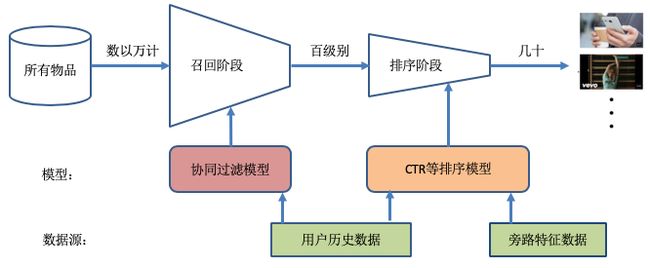
现代推荐系统的架构一般都如下图所示:
花椒推荐系统也采用了同样的架构,整体结构分为召回和排序两部分,整个过程就是从大量的物品集合中精选几十个推荐给用户。我们上述介绍的一系列深度协同过滤模型都是召回阶段算法,但是采用 BPR 作为损失函数的模型也具有 pair-wise 排序功能。
花椒推荐系统的召回算法主要采用 NeuMF 算法,经过多轮超参调整和模型结构调整,我们最终采用了 BPR 损失函数,BPR 比交叉熵损失函数效果有略微提升。需要注意的是,花椒数据集的规模比 movielens 1m 大很多,常规的单机程序已经满足不了效率要求,我们采取了目前分布式计算中较为流行的 Spark 工具来进行数据集的生成和处理,处理完成后的数据集存储在 HDFS 上。在训练阶段,单机多显卡的配置也满足不了 TensorFlow 训练的要求,因此我们采用了 360 私有云的 HBOX 分布式训练平台来完成日常深度模型的训练。
六、总结
本文首先介绍了传统基于相似度的协同过滤算法,然后引申出基于矩阵分解的广义协同过滤,现在推荐系统用到的协同过滤算法几乎都是基于矩阵分解进行的各种优化和扩展。由于算法的需要,需要把推荐问题建模成不同的机器学习模型,他们分别是回归模型、分类模型、BPR 模型,针对这些模型有不同的损失函数来描述他们。
本文重点介绍了目前学术界一些比较好的深度协同过滤算法,介绍了实施这些算法的评估方法、负采样、优化器的选择等方面,然后针对每个算法,都从模型的构建过程,损失函数的选择,模型的结构,以及模型的求解等方面作了简单介绍,为了方便读者尝试和实践,我们都用 TensorFlow 描述了算法的基本结构。由于篇幅所限,每个算法都浅尝辄止,感兴趣的同学可以阅读文后的参考文献中的论文,详细了解算法背后的原理。
参考文献
[1] He, X., Liao, L., Zhang, H., Nie, L., Hu, X., & Chua, T.-S. (2017). Neural Collaborative Filtering. WWW 2017. https://doi.org/10.1145/3038912.3052569
[2] He, X., Du, X., Wang, X., Tian, F., Tang, J., & Chua, T. S. (2018). Outer product-based neural collaborative filtering. IJCAI International Joint Conference on Artificial Intelligence, 2018–July, 2227–2233.
[3] Xue, H., Dai, X., Zhang, J., Huang, S., & Chen, J. (2015). Deep Matrix Factorization Models for Recommender Systems, 3203–3209.
[4] Xu, J., Academy, C., & He, X. (2018). Deep Learning for Matching in Search and Recommendation. WWW 2018 Tutorial
登陆官网了解更多 TensorFlow 搭建推荐系统内容,可登录 B 站 Google 中国 TensorFlow 频道观看《使用 TensorFlow 搭建推荐系统系列(全八讲)》视频,也可关注 TensorFlow 官方公众号获取更多资讯。