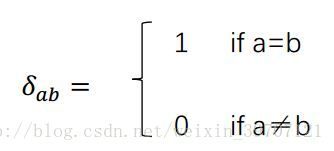Hopfield神经网络处理TSP问题
TSP问题简介:
TSP问题就是在一城市集合{A,B,C,…}中找出一个最短且经过每个城市各一次并回到起点的路径。为了将TSP问题映射到一神经网络的动态演化过程,首先必须找到一合适的表示方法。任一城市在最终路径上的次序可用一N维矢量表示。以10城市为例,如果城市A是第6个访问,则可以用0000010000,即只有第6个神经元的输出为1,其余都是0。为了表示表示所有城市,就需要N×N阶矩阵。例如5个城市,访问顺序顺序是CAEBD,那么可以用这样的方阵表示。
问题解决方案:
对于走过的每一条可能的路径,每个城市都只能走过一次且需要一一走过每个城市,因此这一方阵中的每一行和每一列都只能有一个元素为1,其余元素为0。这边是TSP问题的约束条件。具有上述约束条件的每一路径可用一换位阵表示。
将TSP问题映射为神经网络动力系统可用以下步骤完成:
1) 将TSP问题的每一条可能路径用一换位矩阵表示,并给出相应的距离表示试;
2) 将TSP问题的换位阵集合与由N个神经元构成的神经元阵列相对应;每一条路径所对应的换位阵的各元素与相应的神经元稳态输出对应;
3) 找出一反应TSP约束优化问题的能连函数E;
4) 求出使E取极小值的神经网络连接权重矩阵和偏置参数。
由上述步骤设计的神经网络可用于相应TSP问题的求解,网络的稳态输出即就是TSP问题的局域优化解,同时也是能量函数的极小点。网络的搜索时间即就是网络到达稳态的时间,计算过程也就是网络的动力学过程。
1985年Hopfield和Tank用Hopfield网络求解N=30的TSP问题,使用900个神经元组成的网络在0.2秒时间内找到一个次优解(在10的30次个可能的解中排除10的23次幂个非最优解),从而创建了神经网络优化的新途径。基本思想是:将TSP映射到一神经网络上,通过网络的动力学方程自动演化到网络的平衡态,自动搜索到局部最优解。
连续型Hopfield神经网络解决组合优化问题:Hopfield和Tank意识到,用这种基本的神经网络组织形式,选择好能够恰当表示要被最小化的函数和期望的状态的权重和外部输入,便可以计算出解决特定优化问题的方法。根据微分方程来更新神经元确保了能量函数和优化问题可以同时被最小化。神经元的模拟性质和更新过程的硬件实现可以结合起来,创建一个快速而强大的解决方案。
使用Hopfield神经网络解决TSP问题时,就相当于将需要最小化的目标函数和作为惩罚项的约束共同组成能量函数方程。
二值决策变量定义如下:当城市i在位置j时, =1,其他情况则为0。 代表的是城市i和城市j的距离。目标函数是
第一步是使用惩罚参数方法构建完整优化问题的能量函数表示,所以所有需要最小化的目标函数和惩罚都会被整合成一个单独的函数。这是通过观察![]()
的约束可以通过确保数量的最小化来实现的:

这个约束要求每一列只有一个1,那么这项将被最小化为0。如果每列中多余一个1,这项将会大于0。同样的,每行中1的个数也不能多余一个,以此添加另一惩罚项。因为要确保每行每列都有且只有一个1,所以还要添加一个惩罚项,具体是遍历所有节点后,1的总数是N。由此我们写出TSP问题的能量函数形式:
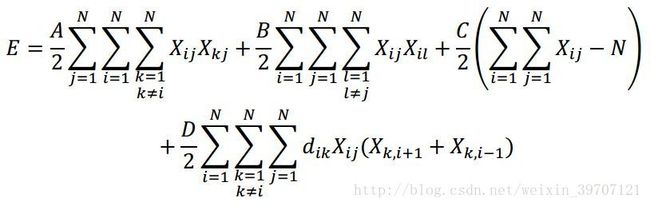
前三项是约束项,最后一项是目标函数。惩罚参数A,B,C和D需要是固定值。这些值反映了这几项在最小化过程中的相对重要性。如果A,B和C相对于D不够大,解决方案可能是不可行的。如果D不够大,解决方案可能是可行的,但旅行商行走路径长度可能会大于最佳值。Hopfield使用了A=B=D=500,C=200这组参数来平衡这些项。
下一步是导出Hopfield网络权重和外部输入,使网络动态能量函数最小化。这里我们需要扩充并重组Hopfield网络标准能量函数方程:

一旦将TSP问题能量函数和Hopfield网络标准能量函数对应起来,网络权重和偏置可以分别被看做二次系数和线性项。为了确保这两个函数的等价性,TSP能量函数中每个项的总和需要在所有相关维度上扩展(i,j,k,l为二次项,i,j为线性项)。因此Kronecker-Delta符号被引入:
展开TSP问题能量函数,将项重新排列成二次、线性和常量项,得到以下形式:
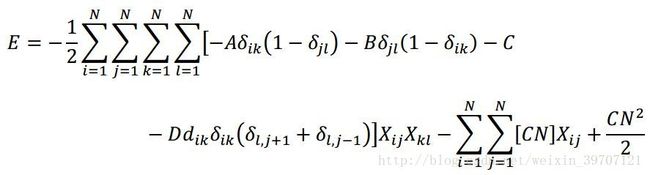
通过将上式和Hopfield网络标准能量函数对照得到权重和偏重表示:
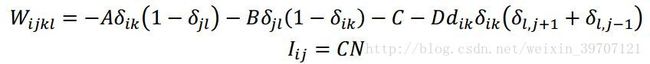
TSP能量函数中的常数项可以被省略,因为它仅仅反映了能量函数向增大方向的移动,不影响函数的最小值的位置。
现在网络权重和外部输入均已被确定,可以开始最小化了。根据连续性Hopfield神经网络演化方程来更新网络状态,若是离散型就用最上面的式子来进行更新。用这种更新方法保证了网络的能量函数可以被最小化,由于是和TSP能量函数对应的,所以结果矩阵X将会为TSP问题提供一个局部最小值。这个解的质量和可行性取决于惩罚参数A、B、C和D的选择,以及神经元的初始化,以及如果选择连续模型演化方程的动力学模拟的准确性。
过程总结:
(1)使用惩罚参数方法为优化问题构建能量函数,然后扩展能量函数,推断出神经网络中的权重和外部输入;(2)将神经元状态初始化为随机值,选好参数ABCD,选好连续激活函数的参数T,如果模拟模拟连续模型还需选好离散时间步长的值;(3)如果能量函数收敛到局部最小值,那么到步骤5,否则执行步骤4;(4)随机选择一个神经元i更新,使用演化方程去更新 和 ;(5)回到步骤3;(6)检验最终的权重矩阵并确定其可行性和最优性;(7)如果想要得到满意结果,调整参数ABCD,重初始化神经元状态,回到步骤3。
很显然,H-T方法解决组合优化问题最大的限制是很难选择合适的惩罚参数。除了这个困难,Hopfield网络的动力学方程是对能量函数进行梯度下降,从而收敛到它们所遇到的第一个局部极小值。由于这两个限制,似乎使用Hopfield网络处理问题的结果质量不高。Wilson和Pawley在1988年公布这些发现,他们对H-T方法解决优化问题的有效性提出了严重的怀疑。
已经提出的Hopfield网络的改进大致可以分为确定性和随机性两类。确定性方法包括特定问题的增强,例如 “divide and conquer(分治算法)”方法来解决TSP;确定性爬山算法例如“rock and roll”;使用替代神经元模型,例如Amartur等人使用的“winner-take-all(赢者通吃粗略)”。
大规模TSP问题的求解:
虽然用Hopfield网络求解大规模TSP问题十分困难,然而处理N=10或20个城市则比较容易。一个自然的想法是把N>100的TSP问题先用分类算法分成若干子类,每一子类10~20个城市,然后把每一个子类看成类似于城市的一个区,再用神经网络求每一区的TSP。而各城区之间的连接也将是一个较小的规模的TSP。用这种分类和分级的方法可使神经网络有效地用于大规模TSP问题的求解。实践证明这一方法也适用于其他的大规模组合优化问题。
Reference:
1.
Potvin J Y, Smith K A. Artificial neuralnetworks for combinatorial optimization[M]//Handbook of metaheuristics.Springer US, 2003: 429-455.
2.《神经网络计算》焦李成
[动词]. 参考