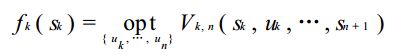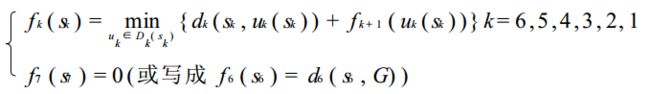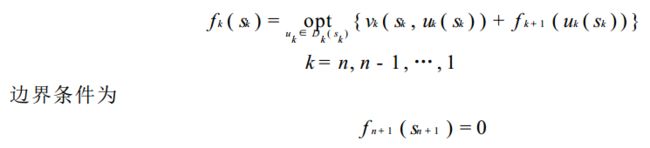从运筹学和算法的角度综合介绍动态规划
算法分类总结
动态规划与静态规划的关系
浅析静态规划和动态规划
动态规划解非线性规划问题(静态规划问题)
规划论:线性规划、非线性规划、动态规划等概念整理
Mathematical optimization
Convex programming
Linear programming
Dynamic programming
线性规划、动态规划等几个概念
教你彻底学会动态规划——入门篇
教你彻底学会动态规划——进阶篇
算法-动态规划 Dynamic Programming--从菜鸟到老鸟
算法进阶之动态规划
算法导论-----动态规划是什么
剑指Offer——动态规划算法
Optimal substructure
Bellman equation
规划论 Mathematical Programming / Mathematical Optimization
规划论是运筹学 (operations research) 的一个分支。
In mathematics, computer science and operations research, mathematical optimization or mathematical programming, alternatively spelled optimisation, is the selection of a best element (with regard to some criterion) from some set of available alternatives.
线性规划 Linear Programming
非线性规划 Nonlinear Programming
随机规划 Stochastic Programming
线性规划 Linear Programming
Convex optimization is a subfield of optimization that studies the problem of minimizing convex functions over convex sets.
Linear programming (LP), a type of convex programming, studies the case in which the objective function f is linear and the constraints are specified using only linear equalities and inequalities. Such a constraint set is called a polyhedron or a polytope if it is bounded.
动态规划 Dynamic Programming
Dynamic programming is both a mathematical optimization method and a computer programming method.
将复杂多阶段问题分解为多个相互联系的单阶段问题,通过求解每个单阶段问题,完成问题求解。
动态规划主要用于求解一时间划分阶段的动态过程的优化问题。(对于一些与时间无关的问题,若果人为地引进时间因素,把它视为多阶段决策过程,也可以用动态规划的方法求解。)
动态规划常常适用于有重叠子问题和最优子结构性质的问题,动态规划方法所耗时间往往远少于朴素解法。
动态规划是一种方法,考察问题,解决问题的一种途径,不是一种具体的,特殊的算法。没有统一的标准模型,也没有构造模型的通用方法,甚至没有判断一个问题能否构造动态规划模型的准则。我们需要对每类问题进行具体分析,构造具体的模型。对于较复杂的问题在选择状态,决策,确定状态转移规律等方面需要丰富的想象力和灵活的技巧性,这就带来了应用上的局限性。
动态规划可分为:
- 线性动态规划
拦截导弹,合唱队形,挖地雷,建学校,剑客决斗等; - 区域动态规划
石子合并, 加分二叉树,统计单词个数,炮兵布阵等; - 树形动态规划
贪吃的九头龙,二分查找树,聚会的欢乐,数字三角形等; - 背包动态规划
背包问题,完全背包问题,分组背包问题,二维背包,装箱问题,挤牛奶
静态与动态
并没有静态规划这个名词,只有动态规划。
动态这个词的来源 - The word dynamic was chosen by Bellman to capture the time-varying aspect of the problems, and because it sounded impressive.
动态规划 Dynamic Programming & 分治策略 Divide and conquer
都是一种 paradigm,范式,方法,思想,分析问题的模式。
动态规划和分治策略类似,都是通过拆分原问题为子问题,求解子问题来求解原问题的。
分治策略将问题划分为互不相交的子问题(独立子问题),递归的求解子问题,再将它们的解组合起来,求出原问题的街。而动态规划与之相反,动态规划应用于子问题重叠的情况,即不同的子问题具有公共的子子问题(子问题的求解释递归进行的,将其划分为更小的子子问题)。面对重叠子问题,分支策略会做重复的工作,他会反复求解公共子子问题,而动态规划对于每个子子问题只求解一次,将其解保存起来,从而不需重复计算求解公共子子问题,避免了大量工作。
核心属性 Key Attribute
There are two key attributes that a problem must have in order for dynamic programming to be applicable: optimal substructure and overlapping sub-problems.
最优子结构
In computer science, a problem is said to have optimal substructure if an optimal solution can be constructed from optimal solutions of its subproblems.
在计算机科学中,如果可以从其子问题的最优解构造最优解,则认为问题具有最优子结构。重叠子问题
In computer science, a problem is said to have overlapping subproblems if the problem can be broken down into subproblems which are reused several times or a recursive algorithm for the problem solves the same subproblem over and over rather than always generating new subproblems.
在计算机科学中,如果问题可分解为会被多次重复使用的子问题,或者问题的递归算法一遍又一遍地解决相同的子问题而不是总是生成新的子问题,则称问题具有重叠的子问题。
数学最优化
In terms of mathematical optimization, dynamic programming usually refers to simplifying a decision by breaking it down into a sequence of decision steps over time.
从数学最优化角度,动态规划通常是指通过将决策分解为一系列决策步骤来简化决策。
This is done by defining a sequence of value functions V1, V2, ..., Vn taking y as an argument representing the state of the system at times i from 1 to n.
通过定义一系列值函数,V1, V2, ..., Vn ,使用 y 来表示系统在时间 / 阶段 i 从 1 到 n 的状态。
(times 这里表示为阶段,state 为状态)
The definition of Vn(y) is the value obtained in state y at the last time n. The values Vi at earlier times i = n −1, n − 2, ..., 2, 1 can be found by working backwards, using a recursive relationship called the Bellman equation.
Vn(y) 的定义是在 n 阶段 y 状态获得的值。对于阶段 i = n −1, n − 2, ..., 2, 1 中 Vi 的值可以向后计算,使用 Bellman equation 递归关系。
For i = 2, ..., n, Vi−1 at any state y is calculated from Vi by maximizing a simple function (usually the sum) of the gain from a decision at time i − 1 and the function Vi at the new state of the system if this decision is made.
对于处于任何 y 状态的阶段 i = 2, ..., n, Vi−1 计算自 Vi,通过取一个简单函数的极值(最简单的情况就是相加),此函数是关于阶段 i − 1 的决策和在新的状态下 Vi 的函数。
Since Vi has already been calculated for the needed states, the above operation yields Vi−1 for those states.
当 Vi与所需的状态相关 (适合于所需的状态)(被设计好了),而之前的操作 Vi−1 也与所需的状态相关了(设计好了)。
Finally, V1 at the initial state of the system is the value of the optimal solution.
最后,处于系统初始状态的 V1 是最优解的值。
The optimal values of the decision variables can be recovered, one by one, by tracking back the calculations already performed.
通过追溯已经执行的计算,可以逐个恢复决策变量的最佳值。
动态规划(一):动态规划的基本概念和基本方程
https://blog.csdn.net/u013527937/article/details/53140686
将所给问题的过程,恰当的分为若干相互联系的阶段,以便能按一定的次序求解问题。阶段的划分一般是根据时间和空间的特征进行的,但是要能够把问题的过程转化为多阶段决策问题。
阶段
将所有问题的过程,恰当的分为若干相互联系的阶段 ,以便能按一定的次序求解问题。阶段的划分一般是根据时间和空间的特征进行的,但是要能够把问题的过程转化为多阶段决策问题。
状态 State
状态表示每个阶段开始所处的自然状态或者客观条件。
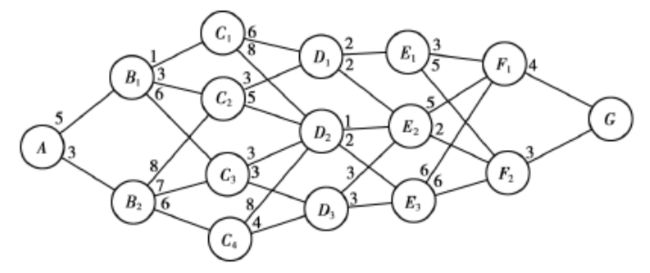
比如在最短线路问题中,线路网络图如下:
途中连线的数字表示花费,问题是求得一条从A到G的最小花费路线。这个问题里,状态就是某阶段的出发位置(比如我们现在在阶段 C,要确定到达阶段 D 的线路)。
这里需要假设路线是有向的(有向无环),从一个阶段到下一个阶段,A->B->C->D->E->F->G。若是无向有环图,便采用 Dijkstra 算法。通常一个阶段有多个状态,第一阶段的状态就是 A,第二阶段的状态就是 {B1, B2},即第 i 阶段所有出发点的集合。
描述状态的变量成为状态变量 state variables,可用一个数,一组数,或是一个向量来描述,常用 Sk (S 表示 State 状态)来表示第 k 阶段的状态变量。如 S3 = {C1, C2, C3, C4} 就表示上例中第 3 阶段的可达状态集合,用 sk 表示第 k 阶段实际取得的状态。(这里,在之前的 Wikipedia 的描述中,可以用 Yi 来表示第 i 阶段的状态变量。如 Y3 = {C1, C2, C3, C4} 就表示上例中第 3 阶段的可达状态集合,用 yi 表示第 i 阶段实际取得的状态。)
这里说的状态有个重要的性质:无后效性(马尔科夫性),即过去的历史只能通过当前的状态去影响他未来的发展,当前状态是以往历史的一个总结,在设计的时候,注意无效性这一点,不能仅有描述过程的具体特征一点规定状态变量,要充分注意是否满足无后效性。
决策 Decision
In definite iteration, control variables are variables which are successively assigned (or bound to) values from a predetermined sequence of values.
在定义的迭代中,决策变量 (control variables) 是变量,这些变量是连续分配的值,而值来自之前已确定(上一个阶段已经确定)的值序列。(决策和决策变量分别是 decision 和 control variables 是因为 The Bellman equation was first applied to engineering control theory and to other topics in applied mathematics, and subsequently became an important tool in economic theory,应用于不同的领域,导致名称无法统一)
决策表示当过程处于某一阶段某一状态时,可以做出的决定,从而确定下一阶段的状态,这个决定就叫做决策。描述决策的变量,成为决策变量 Control variable。可以是一个数,一组数,也可以是一个向量。常用 uk(sk) (可能是 utility 的意思,the state of being useful, profitable, or beneficial)表示处于 k 个阶段处于 sk 时的决策变量,可见决策变量时状态的函数,也就是处于不同的状态时的决策与当前状态有关。(这里,之前 Wikipedia 的描述太过简单,省略了决策和决策变量)。实际问题中,决策变量的取值常常限制在某一范围内,此范围成为允许决策集合,常用 Dk(sk) (D 表示 Decision)表示,显然有 uk(sk) 属于 Dk(sk),如上面的例子中,若从 B1 出发,允许决策集合 D2 = {C1, C2, C3},接下来如果选择 C2,则 u2(B1) = C2。 相关的值也就通过值函数 value function 得到(之后会看到)(就是在之前的 Wikipedia 的描述中,Vn(y) ,定义的是在 n 阶段 y 状态获得的值)。
-
策略 Policy
The dynamic programming approach describes the optimal plan by finding a rule that tells what the controls should be, given any possible value of the state.
动态规划方法通过找到一个规则来描述最佳决策,该规则告诉决策应该是什么,在给定任何可能的状态的值。Such a rule, determining the controls as a function of the states, is called a policy function.
将决策确定为状态的函数的这种规则称为策略函数。 policy function 的解是决策。(以下这段需要忽略中文名词,关注于所表达的含义和公式。)
由过程的第k阶段开始到终止状态为止的过程,称为问题的后部子过程(或称为k子过程)。由每段的决策按照顺序排列组成的决策函数序列 {uk(sk), uk+1(sk+1), … , un(sn)} 称为k子过程策略,简称为子策略,记为 pk,n(sk) 。当 k = 1 时,该决策序列称为全过程的一个策略,简称策略,即 p1,n(s1) 。同样的可以定义允许策略集合,其中达到最优效果的称为最优策略。(p1,n(s1) 表示从阶段 1 开始所有可能的状态选择的函数,解为 decision, 最优的 decision 所对应的 state 的选择就是最优策略,最优需要通过分析指标函数的解所确定的最优值函数来决定。) -
指标函数和最优值函数 objective function & value function
First, any optimization problem has some objective: minimizing travel time, minimizing cost, maximizing profits, maximizing utility, etc. The mathematical function that describes this objective is called the objective function.
任何最优问题都有目标,最大或是最小等,描述这种目标的数学公式成为 objective function 指标函数。The best possible value of the objective, written as a function of the state, is called the value function.
最可能的目标的值,写成状态的函数,被称为 value function 最优值函数。value function 的解是目标值。指标函数 objective function 即用来衡量所实现过程优劣的数量指标,它定义在全过程和所有后部子过程上确定的数量函数,用 Vk,n 表示,即 Vk,n = Vk,n(sk, uk, sk+1, uk+1, … , sn+1) , k = 1, 2, …, n。该指标函数应该具有可分离性,并满足递推关系,即Vk,n可以表示为sk,uk,Vk+1,n的函数。常见的指标函数有(1)过程和它的任一子过程的指标是它所包含的各个阶段的指标的和;(2)过程和它的任一子过程的指标是它所包含的各个阶段的指标的乘积。
最优值函数 value function 是指标函数的最优值,记为 fk(sk),表示从第 k 阶段的状态开始到第 n 阶段的终止状态的过程,采取最优策略所得到的指标函数值(一般是最大/最小值),即:
-
状态转移方程 Bellman equation (动态规划方程)
Richard Bellman showed that a dynamic optimization problem in discrete time can be stated in a recursive, step-by-step form known as backward induction by writing down the relationship between the value function in one period and the value function in the next period.
Richard Bellman 表明,一个具有分离时间属性(具有不同阶段)的动态最优问题可以通过写出 一个阶段的 value function 和下一个阶段的 value function 之间的关系来声明为逐步形式的递归,也就是backward induction 反向归纳。The relationship between these two value functions is called the "Bellman equation".
两个 value functions 之间的关系别成为 Bellman equation。(value function 是状态的函数)状态转移方程是 value functions 之间的关系,也是确定过程由一个状态到另一个状态的演变过程(因为 value function 是状态的函数)。由前面的讨论我们知道,如果给定第 k 个阶段的状态变量 sk 的取值,那么该阶段的决策变量 uk(sk) 一经确定,第 k+1 阶段的状态变量 uk+1(sk+1) 的取值也就决定了。即 sk+1 的值随 sk 和 uk 的值变化而变化,这种对应关系,记为:sk+1 = Tk(sk, uk),称之为状态转移方程,Tk为状态转移函数,在上例中,状态转移方程就是:sk+1 = uk(sk) (uk(B1) = C2)。
案例分析
以解决最短路径问题介绍动态规划的基本思路。
在最短路径问题中,如果 A->B1->C2->D1->E2->F2->G 是从 A 到 G 的最短路线,那么 D1->E2->F2->G 也就是 D1 到 G 的最短路线。即如果由起点 A 经过 P 点 和 H 点而到达终点 G 是一条最短路径,则由 P 出发经过 H 而到达 G 点的这条子路径,也必定是 P 点 到达 G 点的最短路径。求出各点到 G 点的最短路径,再求出 A 点到 G 点的最短路径。所以,这道题可以使用动态规划从终点逐段向起点方向寻找最短路线。
下面按照动态规划的方法,从最后一段开始计算,由后向前逐步推移至A点。(直接附书上方法了,了解思想后这个比较容易)
最短路线在按照计算顺序的反方向(按阶段顺序)反推就可以了(如 A 到 G 的最短路线是通过 B1 得到的),很容易得到最短路线为 A->B1->C2->D1->E2->F2->G。
在上面的计算过程中可以看出,在求解的各个阶段,我们利用了 k 阶段与 k+1 阶段之间的递推关系:
一般情况下,k 阶段和 k+1 阶段的递推关系式可写为(注意边界条件):
其中 vk(sk, uk(sk)) 表示第 k 阶段作出决策 uk(sk) 时的阶段指标(对比上面的最短路径问题的递推式)。上面的递推关系式就是动态规划问题的基本方程。
基本思想
- 动态规划的关键在于正确地写出基本的递推关系式和恰当的边界条件(也就是基本方程)。因此,必须将问题的过程划分为几个相互联系的阶段,选取恰当的状态变量,决策变量以及定义最优值函数,从而把一个大问题化为一系列同类型的子问题,然后逐个求解。即从边界条件开始,逐渐递推寻优,在每一个子问题的求解中,均利用了它前面子问题的最优化结果,依次计算,最后一个子问题所得的最优解,就是整个问题的最优解。
- 在多阶段决策的过程中,动态规划方法是即把当前一段和未来各段分开,又把当前效益和未来效益结合起来考虑的一种最优化方法。因此,每段决策的选取是从全局来考虑的,与该段的最优选择答案一般不同。(贪心?)
- 在求整个问题的最优策略时,由于初始状态时已知的,而每段的策略都是该段状态的函数,故最优策略所经过的各段状态都可以主次逐次变换得到,从而确定了最优路线。
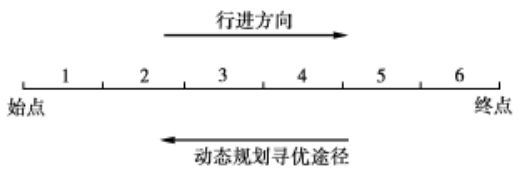
上面的解法称为逆序解法,如果我们把 G 点作为起点,A 点作为终点,则得到了顺序解法(思想一样,不做赘述)。但是动态规划的求解方向都与行进方向是相反的。
动态规划问题特性
适用动态规划的问题必须满足最优化原理和无后效性。
1.最优化原理 (Principle of optimality == Bellman equation)(最优子结构性质,非最优子结构) 最优化原理可这样阐述:一个最优化策略具有这样的性质,不论过去状态和决策如何,对前面的决策所形成的状态而言,余下的诸决策必须构成最优策略。简而言之,一个最优化策略的子策略总是最优的。一个问题满足最优化原理又称其具有最优子结构性质。
2.无后效性将各阶段按照一定的次序排列好之后,对于某个给定的阶段的状态,它以前各阶段的状态无法直接影响它未来的决策,而只能通过当前的这个状态。换句话说,每个状态都是过去历史的一个完整总结。这就是无后向性,又称为无后效性,即马尔科夫性。
动态规划算法设计
This can be achieved in either of two ways:
- 自顶向下 Top-down approach (又称记忆化搜索、备忘录)
基本上对应着递归函数实现,从大范围开始计算,要注意不断保存中间结果,避免重复计算 - 自底向上 Bottom-up approach (递推)
从小范围递推计算到大范围
- (4) 正确写出状态转移方程 ;
解题思路
- 分解原问题为子问题(划分阶段)
把原问题分解为若干个子问题,子问题与原问题形式相同或类似,只不过规模变小了。解决子问题,原问题即解决。 - 确定状态 Sk
状态,在某个阶段,子问题相关的各个变量的一组取值。
状态需要既能描述过程的演变,又要满足无后效性。
在用动态规划解题时,我们往往将和子问题(阶段)相关的各个变量的一组取值,称之为一个“状态”。一个“状态”对应于一个或多个子问题, 所谓某个“状态”下的“值”,就是这个“状态”所对应的子问题的解。
所有“状态”的集合,构成问题的“状态空间”。“状态空间”的大小,与用动态规划解决问题的时间复杂度直接相关。 - 确定决策变量 uk 及每阶段的允许决策集合 Dk(sk) ;
- 确定边界条件(初始状态)
- 确定状态转移方程
定义出什么是“状态”,以及在该“状态”下的“值”后,就要找出不同的状态之间如何迁移――即如何从一个或多个“值”已知的 “状态”,求出另一个“状态”的“值”(递推型)。 - 正确写出指标函数 Vk,n
指标函数应满足三个形式:- 是定义在全过程和所有后部子过程上的函数
- 具有可分离型,并满足递推关系。 即 Vk,n(sk , uk , … , sn+1) = ψk[sk , uk ,Vk+1,n(sk+1 , uk+1 , … , sn+1)]
- 函数 ψk(sk , uk, Vk+1,n) 对于变量 Vk+1,n 要严格单调。
例子
爬楼梯问题
Fibonacci series
Bellman–Ford algorithm
动态规划的经典模型
特点
动态规划将原来具有指数级时间复杂度的搜索算法改进成了具有多项式时间复杂度的算法。其中的关键在于解决冗余,这是动态规划算法的根本目的。动态规划实质上是一种以空间换时间的技术,它在实现的过程中,不得不存储产生过程中的各种状态,所以它的空间复杂度要大于其它的算法。