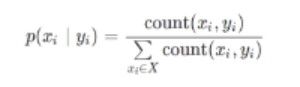文本处理一直是算法学习重要组成,本文对字符串的相似性,可读性做简单记录。
01 字符串相似性
评价字符串相似度最常见的办法就是:把一个字符串通过插入、删除或替换这样的编辑操作,变成另外一个字符串,所需要的最少编辑次数,这种就是编辑距离(edit distance)度量方法,也称为Levenshtein距离。
hamming 海明距离是编辑距离的一种特殊情况,只计算等长情况下替换操作的编辑次数,只能应用于两个等长字符串间的距离度量。
其他常用的度量方法还有 Jaccard distance、J-W距离(Jaro–Winkler distance)、余弦相似性(cosine similarity)、欧氏距离(Euclidean distance)等。
def domian_similarity():
str1 = "我的骨骼雪白 也长不出青稞"
str2 = "雪的日子 我只想到雪中去si"
# 1. difflib
seq = difflib.SequenceMatcher(None, str1,str2)
ratio = seq.ratio()
print('difflib similarity1: ', ratio)
# difflib similarity1: 0.14814814814814814
# difflib 去掉列表中不需要比较的字符
seq = difflib.SequenceMatcher(lambda x: x in ' 我的雪', str1,str2)
ratio = seq.ratio()
print('difflib similarity2: ', ratio)
# difflib similarity2: 0.0
# 2. hamming距离,str1和str2长度必须一致,描述两个等长字串之间对应位置上不同字符的个数
str1 = 'ztcqcffho.com'
str2 = 'kplzhxzcz.com'
hamsim = Levenshtein.hamming(str1, str2)
print('hamming similarity: ', hamsim)
# hamming similarity: 9
# 3. 编辑距离,描述由一个字串转化成另一个字串最少的操作次数,在其中的操作包括 插入、删除、替换
sim = Levenshtein.distance(str1, str2)
print('Levenshtein similarity: ', sim)
# Levenshtein similarity: 9
# 4.计算莱文斯坦比
ratiosim = Levenshtein.ratio(str1, str2)
print('Levenshtein.ratio similarity: ', ratiosim)
# Levenshtein.ratio similarity: 0.46153846153846156
# 5.计算jaro距离
jarosim = Levenshtein.jaro(str1, str2)
print('Levenshtein.jaro similarity: ', jarosim)
# Levenshtein.jaro similarity: 0.5732600732600731
# 6. Jaro–Winkler距离
jaro_winklersim = Levenshtein.jaro_winkler(str1, str2)
print('Levenshtein.jaro_winkler similarity: ', jaro_winklersim)
# Levenshtein.jaro_winkler similarity: 0.5732600732600731
# 字符串处理
test1 = ['你好', '我是谁']
test2 = ['你好', 'woshi']
difflib.SequenceMatcher(a=test1, b=test2).quick_ratio() # 0.5 # difflib使用时不一定为字符串,但匹配时只有单个元素完全匹配才计入
difflib.SequenceMatcher(a=test1, b=test2).ratio() # 0.5
Levenshtein.distance(','.join(test1), ','.join(test2)) # Levenshtein则需要输入为字符串,匹配时是整体匹配
02 可读性
现实世界中有一类问题具有明显的时序性,比如路口红绿灯、连续几天的天气变化,我们说话的上下文···,隐马尔可夫模型(Hidden Markov Model,HMM)都有很好的应用,以下文文本可读性的算法。
2.1、文本处理
以下文本为模型的训练文本,模型通过学习正常语言规律的文本,获得文本的可读特征。将文本处理成应用算法的数据形式:
对以上文本做2gram处理,例如 "Well, some hundreds of times."经过2gram处理后为 ['we', 'el', 'll', 'l ', ' s', 'so', 'om', 'me', 'e ', ' h', 'hu', 'un', 'nd', 'dr', 're', 'ed', 'ds', 's ', ' o', 'of', 'f ', ' t', 'ti', 'im', 'me', 'es'] ,全文中'we' 出现15064次。
计算每种组合的发生概率,log处理后数据如下:
2.2、转移概率
例如以下‘ two models ’经2Gram处理后,为9组:
log_prob = log(P('tw')) + log(P('wo')) + log(P('o ')) + log(P(' m')) + log(P('mo')) + log(P('od')) + log(P('de')) + log(P('el')) + log(P('ls')) = -5.2+ -2.5 + -2.2 + -3.4 + -2.2 + -4.1 + -2.0 + -3.4 + -3.9 = -28.9
probably = math.exp(log_prob / 9) = 0.04
如下所示,复合语言可读规律的,概率得分比较高,而不符合可读性的概率得分则比较低。
| 字符串 | 转移概率 |
|---|---|
| some long sentence, might suck? | 0.084 |
| Project Gutenberg | 0.048 |
| How many? I don't know. | 0.065 |
| zxcvwerjasc | 0.008 |
| nmnjcviburili,<> | 0.014 |
| ertrjiloifdfyyoiu | 0.006 |
| grty iuewdiivjh | 0.013 |
模型应用
检验域名是否符合可读性的规律
l = ['qwwzlam.ru','rmqsnln.ru','baidu.com','google.com'],显然结果和预想的一样。
03 参考资料
- Python 字符串相似性的几种度量方法
- Gibberish-Detector
数据标准化处理