原文链接:https://mp.weixin.qq.com/s/wxpYBu-6egd985HcF-dXOQ
上一篇文章我们讲了欧姆定律,温故而知新,在开始讲分压原理之前,把欧姆定律的表达式贴出来,让大家再复习一下。
(其中,V是电压,I是电流,R是电阻)
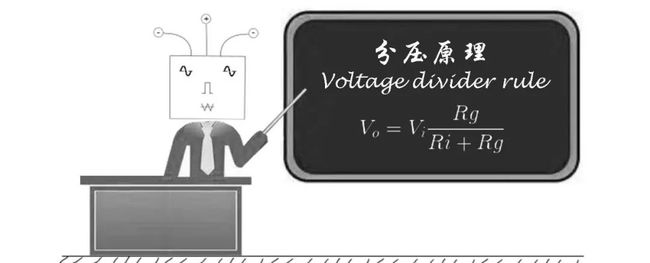
2 分压原理(Voltage divider rule)
分压原理广泛应用于各种电路设计之中,而分压原理也是从欧姆定律推导出来的。那么我们先来看看分压原理的基本表达式:
公式(2-1)
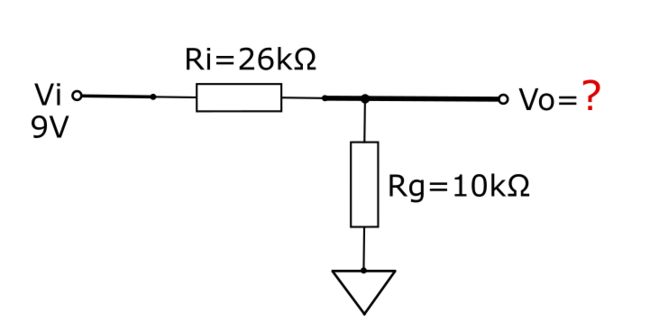
只看公式未免有点枯燥难理解,我们把上图中的电压电阻数值带入公式中,看实际的输出电压Vo是多少。
公式(2-2)
到此,我们就算出了Vo=2.5V的结果。细心的读者还会发现,上面的公式中,我们在计算的时候带着数值的单位量纲,然后再把相同的单位量纲约掉,这是工程计算里面很重要的一个小技巧,它可以让你避免一些低级的失误。
回到我们的分压原理,我们在记忆分压原理的时候,不要把分子Rg搞混,写成Ri了,只要记住Rg里面的g是ground,是“地”的意思,就比较清楚了。
/ 分压原理其实就是欧姆定律 /
那么分压原理怎么从欧姆定律推导出来呢?其实很简单,我们只要把公式(2-1)换另外一个角度来看,你就会发现欧姆定律存在的证据了:
公式(2-3)
我们把Vi的位置和Rg的位置互换了一下,那么就变成了用欧姆定律先求回路电流 I,然后通过欧姆定律得到Vo=I*Rg。但是其实他们还是相同的公式,一点都没变!
从这个角度来看,是不是就清晰很多了?这就是为什么我们要说欧姆定律是电子学里最重要的基础知识!
既然欧姆定律就可以解决的问题,为什么我们要再费劲心思弄出一个分压原理呢?
/ 分压原理的实际意义 /
大家再看看公式(2-2),我们在计算的时候把单位kΩ直接约掉,那么剩下的等式就是一个纯数字常数,在这里,输入Vi和输出Vo就单纯的变成了一个常数比例关系,可以很轻松地看出Vi和Vo的关系。
在电路里我们把这个叫做增益,用大写字母H来表示。所以Vi和Vo的关系可以写成:
(公式2-4)
而这个增益H,也是控制理论里很重要的概念。同时也是我们理解运放的强有力工具(运放的讲解将放在后续文章)。
/ 分压原理的增益H /
细心的你也许注意到了,公式(2-4)中的增益H的范围是0~1,而且永远不会大于1,即H≤1。
从直观上看,当Rg无限接近0时,相当于直接短路到地,即H=0,所以 Vo = 0;而当Rg无限大时,相当于Rg不存在,Ri对地是开路的,即H=1,所以开路电压Vo = Vi 。
从这个角度来看,你就可以使用增益H来规划Vo的输出了。比如公式(2-2)中,就是实际应用中的一个例子,我们要用单片机检测9V的电压,但是单片机的A/D参考电压都是3.3V,所以我们需要把9V降到低于3.3V以下,才能接到单片机的A/D引脚。那么我们就设计了一个增益H=10/36的分压电路,把9V变成了2.5V。
把问题从“用欧姆定律把9V变成2.5V”换做“用分压原理把9V变成2.5V”,是不是更容易理解我们要做的事情呢? 这也是分压原理的一个实际意义吧。
/ 电容是否适用于分压原理? /
如果把上图中靠近地端的电阻Rg换成一个电容,是不是分压原理也适用呢?还记得我们在上一篇文章中最后提到的吗?“电容和电感可以看做是依赖于信号频率的电阻”。那么,这个新组成的分压器,是不是就是一个依赖于信号频率的分压器呢?答案是肯定的!
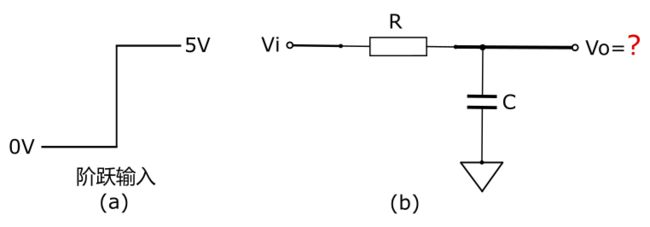
如下图所示,大家把这样的电路称作RC电路:
既然电容可以看成是一个依赖于频率的电阻,那么输出Vo就不能简单的通过纯电阻分压公式(2-1)来求解了。我们试着给RC电路输入一个上图(a)中的阶跃输入,看看会发生什么。
还是初中物理课上,我记得老师对电容的描述是“通交流,阻直流”,那么阶跃输入是交流还是直流呢?我们看到,阶跃输入的电压,从0V瞬间就跃到了5V,电压变化速度非常快。而这个快速变化里面其实包含了很多高频分量(傅里叶变化以后会看到这些高频分量),电容的“通交流”特性,其实就是它对高频信号具有低阻抗的特性。那么我们就可以很容易套入分压原理来解释RC电路在输入阶跃信号以后的电压-时间特性了。如下图所示:
在阶跃输入以后,Vo的数值从零开始,慢慢往上走,直到Vo的值达到5V,最后稳定在5V。
就相当于电容刚开始是对地短路的(电容对高频分量是低阻抗的),然后电容的“阻抗”慢慢变大,一直变大到相当于对地开路(断开了)。因为上面的阶跃输入最后是一直稳定在5V的,也就是变成了一个5V的直流电源,根据电容“阻直流”的特性,电流是不会通过电容的,是不是就是相当于电容和地之间断开了呢?
从图中我们也很直观地看到,电容“阻碍”着电压的变化,电压不是瞬间改变的,需要一段时间才稳定。
这就是典型的RC电路的瞬态响应了!有一个公式用来表达:
公式(2-5)
其中,RC的值被称为时间常数,用 τ (念tao)来表示。
从公式(2-5)中我们看到,套用到公式(2-4)(Vo=Vi x H)中,增益H等同于:
公式(2-6)
因此RC的值,也就是时间常数τ,变成了决定Vo大小的一个常量(时间点也可以看成一个常量),而且这里的H也是不会大于1,那么是不是电容也完美地符合了我们的分压原理!
我们再继续深入发掘,如果把上图中的Y轴归一化为Vo的最终输出电压5V,而X轴变成时间常数τ,结果会怎么样?如下图所示:
在1τ时,电压上升到大约63%,2τ已经达到了87%,3τ是95%,5τ以后就非常接近100%了。
工程上,3τ时间点是一个重要的点,一般认为达到3τ时间点以后,供电电压就稳定了,可以进行下一步的相关操作(初始化,采样等等)。
/ 电感是个什么情况? /
既然电容的描述是“通交流,阻直流”,那么电感是什么呢?我们稍微回忆一下。
对了,就是和电容正好相反的特性——“通直流,阻交流”。然后上面我们谈到的关于电容的特性,只要反一反,就变成了电感的特性了!是不是很简单?
下面我们就总结一下这一对“冤家”的特性:
电容“通交流,阻直流”;电感“通直流,阻交流”;
电容“阻碍电压的变化”;电感“阻碍电流的变化”;
电容对高频信号低阻抗;电感对高频信号高阻抗;
电容时间常数τ=RC;电感时间常数τ=R/L。
这样是不是很直观了?
/ 手拉手 or 肩并肩? /
有这么一种比喻,说电阻的串联就像手拉手,而并联就像肩并肩,然后一起奔向电源?话糙理不糙,这个比喻是有那么一点意思。
对于电阻串联,如下所示:
Rt = R1 + R2 + ... + Rn
简单点说,有一个加一个,有n个,加n个。
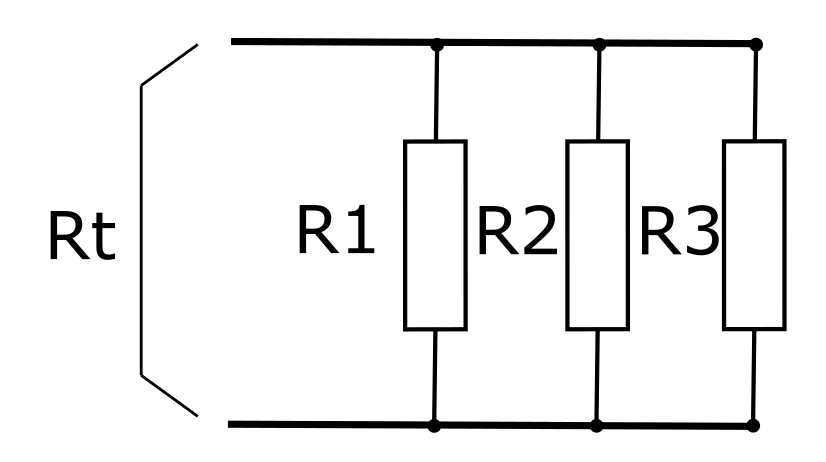
对于电阻的并联,如下所示:
这时候就稍微有点复杂,首先要先求R1//R2,算出结果以后,再求R12//R3。(//表示并联关系)。
并联电阻的求解总结如下:求并联它不能急,一次只能来一对,多了不行!
/ 电容电感的串并联? /
既然知道了电阻的串并联,电容和电感就不在话下了。只要记住下面两点,一切都迎刃而解:
电感的串并联和电阻完全一样;
电容的串联等同于电阻的并联;电容的并联等同于电阻的串联。
我就好奇为啥电容总是喜欢唱反调呢?
到此分压原理和串并联的计算方法我们讲完了。
不要小看电阻、电容、电感这些基础元件,他们可是占据了电子元器件行业的半壁江山,而且只多不少!具体到实际的应用场景,这些基础的元器件也是五花八门:直插的,贴片的,信号的,功率的,高频的等等。
但是记住一点,无论他们具体的名字叫什么,都始终遵循着这些基本的电路原理。所以还是那句话,基础知识是最重要的,无论什么时候强调都不过分:基础知识最重要!
如果我们在本文中第一张电路图里再加入一路电源,如下图所示,那么其输出电压Vo会变成多少呢?
是不是看起来稍微有点复杂了?这就需要用到下篇文章里,我们将会谈到的另外一个重要定理:戴维南定理(Thevenin's theorem),它是分析复杂电路,化繁为简的一把利器。