【论文笔记】VIT：AN IMAGE IS WORTH 16X16 WORDS: TRANSFORMERS FOR IMAGE RECOGNITION AT SCALE

本文简单记录关于视觉transformer模型VIT (AN IMAGE IS WORTH 16X16 WORDS: TRANSFORMERS FOR IMAGE RECOGNITION AT SCALE)的论文笔记和相应的pytorch源码分析

论文及代码地址

论文地址：https://arxiv.org/abs/2010.11929
代码地址：
tensorflow: https://github.com/google-research/vision_transformer
pytorch: https://github.com/lucidrains/vit-pytorch

论文笔记

1. motivation

在视觉任务中，attention机制通常与卷积网络结合发挥作用，或者利用attention机制来替代卷积网络中某些特定的组件，本文抛弃了这种attention与CNN结合的视觉特征学习的范式，而是直接采用transformer进行序列化的学习视觉的特征表达。

本文提到将一张图片划分成不同的patch，然后用线性的embedding表示给定图片，将其输入tranfomer，完成图片的分类任务。本文提出的VIT在大数据集上进行训练，然后将模型迁移到中等或者小的数据集上面进行视觉分类任务。

Transformer相比CNN的缺点：transformer缺少inductive bias，比如CNN的平移不变性，CNN的图像邻域特性，因此训练transforer相比CNN需要更多的数据，来增强模型的泛化能力。同时论文发现，随着训练数据规模的增加，transformer在inductive bias上的损失更小。

2. method

本文采用的transfomer的整体结构与Attention Is All You Need（论文地址：https://arxiv.org/abs/1706.03762）基本一致。
VIT的基本结构见下图：
可以大致分成三部分：

• 输入图片划分成多个patch，然后利用线性变换将不同patch映射成为一个patch embedding.
• 将patch的相对位置信息考虑进patch embedding生成position embedding
• 将position embedding输入transformer encoder最后通过MLP层输出图片所属的类别
  

transformer的encoder包含两部分：multi-head self attention; MLP blocks
2.1 multi-head self attention
一般化（single head）的self attention采用https://arxiv.org/abs/1706.03762的结构，对于每个输入的向量$z\in R^{N\times D}$，我们利用三个不同的线性映射$Uq,Uk,Uv$计算三个不同的矩阵$q,k,v$，分别记做query, key ,value矩阵，attention矩阵的权重$A_{ij}$表示$z$里面任意两个子序列的相似性。其中$Dh$表示缩放系数，通常初始化为$D/k$，k表示attention的head个数。最后的$SA$表示通过self attention转化之后的value矩阵。

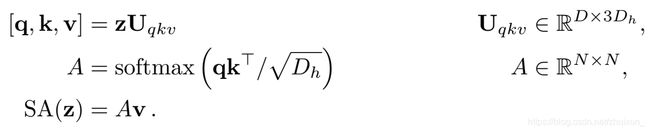
multihead self-attention(MSA) 是上面single self attention的k次组合，之所以采用k次一方面我觉得是增加模型的泛化性能，通过k次不同的映射，可以探索$z$在不同空间的表达形式。

2.2 transforme encoder的具体形式
transforme encoder采用两次残差连接的方式，将第一层的MSA norm之后输入到MLP模块，最后输出encoder的结果
在下面的公式中：
$z_0$表示position embedding的结果
$z_l^{\prime }$ 表示残差输出的multi self attention 模块， $z_{l-1}$ 表示multi self attention的输入
$z_l$ 表示残差输出的MLP 模块， $z_l^{\prime }$ 表示MLP 模块的输入
$y$ 表示layer norm之后的encoder的输出结果

3. results

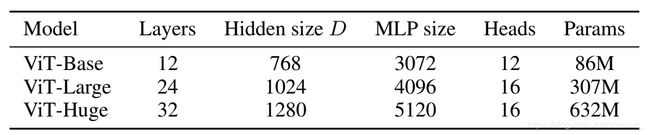
首先给出了VIT的变体，根据不同的layer, hidden size, MLP size, heads的个数，得到VIT的不同量级的模型

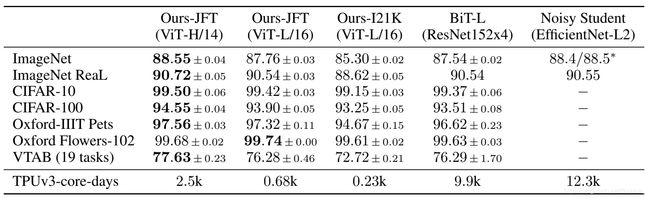
其次在不同的数据集上面对比了BIT和nosiy student的实验结果：
可以发现利用上表中的VIT-huge模型在绝大多数 数据集的分类效果都比较好

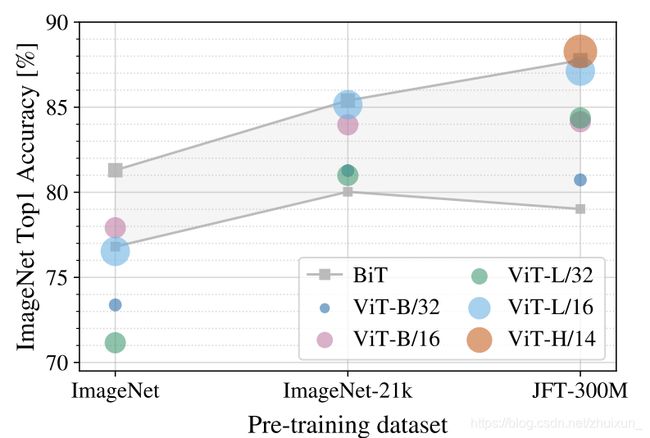
在imagenet上面pretrain的结果：
可以发现VIT在小的数据集上面pretrain的结果不如BIT，但随着pretrain的数据集的规模增加，优势逐渐凸显出来。

不同参数量的VIT与同等条件下的resnet和hybrid方法的对比：
一般来说，在同等计算量(FLOPs)下，transfomer的表现比两者优
在参数量较小的情况下, hybrid方法比transformer表现好，但随着参数量的增加，这种差距逐渐缩小

源码分析

本文分析pytorch 版本的VIT https://github.com/lucidrains/vit-pytorch
首先来看VIT这个类：

1. VIT的实现及初始化：

v = ViT(
        image_size=256, # 输入图片的长和宽
        patch_size=32, # 一张图划分成为多少个子图
        num_classes=1000, # 最后的类别数目
        dim=1024, # 分类前面的squeeze的向量长度，从dim维度映射到num_classes
        depth=6, # transformer encoder堆叠的个数
        heads=16, # head的数目（MSA模块）
        mlp_dim=2048, # transformer encoder中的mlp层的输出维度
        dropout=0.1,
        emb_dropout=0.1
    )

1. 在to_patch_embedding 这个函数里，主要做了两件事：把patch压成一行向量（ Rearrange）；通过线性变换到dim维（self.linear = nn.Linear(patch_dim,dim)）
2. self.cls_token 的作用：表示输入的序列最前面的标志点的信息(0*这个起始位)，和postion embedding分开学习
3. self.pos_embedding：包含torch.randn(1, num_patches + 1, dim)维，加1的原因是记录cls起始位的信息
4. 然后将结果送入transformer和MLP层输出就可以了

class ViT(nn.Module):
    def __init__(self, *, image_size, patch_size, num_classes, dim, depth, heads, mlp_dim, pool = 'cls', channels = 3, dim_head = 64, dropout = 0., emb_dropout = 0.):
        super().__init__()
        assert image_size % patch_size == 0, 'Image dimensions must be divisible by the patch size.'
        num_patches = (image_size // patch_size) ** 2 # num = (256//32)**2 = 64 # patch的个数
        patch_dim = channels * patch_size ** 2  #先计算乘方 后计算乘法 patch_dim = 3 * 32 * 32 每张子图对应的维度
        assert pool in {
     'cls', 'mean'}, 'pool type must be either cls (cls token) or mean (mean pooling)'
        # self.to_patch_embedding = nn.Sequential(
        #     Rearrange('b c (h p1) (w p2) -> b (h w) (p1 p2 c)', p1 = patch_size, p2 = patch_size),
        #     nn.Linear(patch_dim, dim),
        # )
        #输出的维度
        self.rearrange=nn.Sequential(
            Rearrange('b c (h p1) (w p2) -> b (h w) (p1 p2 c)', p1=patch_size, p2=patch_size), # h*p1=image_size=256, p1=32, h= 8
            # 一共有64个patch 这句话把每个patch压缩成了一维张量
        )
        self.linear = nn.Linear(patch_dim,dim) # 将最后一维张量映射成[b, (h,w), (p1,p2,c)] -> [b, (h,w), dim]

        self.pos_embedding = nn.Parameter(torch.randn(1, num_patches + 1, dim)) # 有前导0 为什么position embedding 需要前导0 ？
        self.cls_token = nn.Parameter(torch.randn(1, 1, dim))
        self.dropout = nn.Dropout(emb_dropout)

        self.transformer = Transformer(dim, depth, heads, dim_head, mlp_dim, dropout)

        self.pool = pool
        self.to_latent = nn.Identity()

        self.mlp_head = nn.Sequential(
            nn.LayerNorm(dim),
            nn.Linear(dim, num_classes)
        )

    def forward(self, img):
        # x = self.to_patch_embedding(img)
        x = self.rearrange(img)
        # print(type(x))
        # print(x.shape) # torch.Size([4, 64, 3072])
        # return
        x= self.linear(x) #
        b, n, _ = x.shape # [b, (h,w), dim]

        cls_tokens = repeat(self.cls_token, '() n d -> b n d', b = b)
        x = torch.cat((cls_tokens, x), dim=1) # 把token放在句首

        x += self.pos_embedding[:, :(n + 1)]
        x = self.dropout(x)

        x = self.transformer(x) # self attention + Feedforward

        x = x.mean(dim = 1) if self.pool == 'mean' else x[:, 0]

        x = self.to_latent(x)
        return self.mlp_head(x)

2. transformer的实现：

每个transform包含Attention模块和FeedForward(FFN) 模块：

class Transformer(nn.Module): # transformer的具体实现
    def __init__(self, dim, depth, heads, dim_head, mlp_dim, dropout = 0.):
        super().__init__()
        self.layers = nn.ModuleList([])
        for _ in range(depth):
            self.layers.append(nn.ModuleList([
                PreNorm(dim, Attention(dim, heads = heads, dim_head = dim_head, dropout = dropout)), #(16,64)
                PreNorm(dim, FeedForward(dim, mlp_dim, dropout = dropout))
            ]))
    def forward(self, x):
        for attn, ff in self.layers:
            x = attn(x) + x
            x = ff(x) + x
        return x

Attention模块的实现：
主要还是参考上面transfomer的公式，

1. qkv = self.to_qkv(x).chunk(3, dim = -1) ：将输入的x序列通过不同的线性映射到$q,v,k$矩阵
2. dots = einsum(‘b h i d, b h j d -> b h i j’, q, k) * self.scale ： 得到attention 矩阵$Aij=(q\ast k/sqrt(d_k))$
3. out = einsum(‘b h i j, b h j d -> b h i d’, attn, v) ：得到最后的attention输出$SA(x)=Av$

class Attention(nn.Module):
    def __init__(self, dim, heads = 8, dim_head = 64, dropout = 0.):
        super().__init__()
        inner_dim = dim_head *  heads #
        project_out = not (heads == 1 and dim_head == dim)

        self.heads = heads
        self.scale = dim_head ** -0.5 # 1/sqrt(d_k)

        self.attend = nn.Softmax(dim = -1)
        self.to_qkv = nn.Linear(dim, inner_dim * 3, bias = False) # (Q,K,V)

        self.to_out = nn.Sequential(
            nn.Linear(inner_dim, dim),
            nn.Dropout(dropout)
        ) if project_out else nn.Identity()

    def forward(self, x):
        # self attention 参考链接： https://zhuanlan.zhihu.com/p/82312421
        # ans = softmax(Q*KT/sqrt(d_k))*V
        # Q, K, V 三个变量的作用和意义到底是什么？？
        b, n, _, h = *x.shape, self.heads # x shape[b,n,dim]
        qkv = self.to_qkv(x).chunk(3, dim = -1) # Q: [b,n,dim_head*heads]
        # print(qkv[0].size())

        q, k, v = map(lambda t: rearrange(t, 'b n (h d) -> b h n d', h = h), qkv) # h: head

        dots = einsum('b h i d, b h j d -> b h i j', q, k) * self.scale # (q*k/sqrt(d_k))
        attn = self.attend(dots)
        out = einsum('b h i j, b h j d -> b h i d', attn, v) # sortmax(dots)*V
        out = rearrange(out, 'b h n d -> b n (h d)')

        return self.to_out(out)

FeedForward(FFN) 模块实现：
FFN由多个线性层+dropout实现，具体可看代码：

class PreNorm(nn.Module):
    def __init__(self, dim, fn):
        super().__init__()
        self.norm = nn.LayerNorm(dim)
        self.fn = fn
    def forward(self, x, **kwargs):
        return self.fn(self.norm(x), **kwargs)

class FeedForward(nn.Module):
    def __init__(self, dim, hidden_dim, dropout = 0.):
        super().__init__()
        self.net = nn.Sequential(
            nn.Linear(dim, hidden_dim),
            nn.GELU(),
            nn.Dropout(dropout),
            nn.Linear(hidden_dim, dim),
            nn.Dropout(dropout)
        )
    def forward(self, x):
        return self.net(x)

参考文献

1. https://arxiv.org/abs/2010.11929
2. https://arxiv.org/abs/1706.03762