深度学习基础--线性回归(单层神经网络)
深度学习基础–线性回归(单层神经网络)
最近在阅读一本书籍–Dive-into-DL-Pytorch(动手学深度学习),链接:https://github.com/newmonkey/Dive-into-DL-PyTorch,自身觉得受益匪浅,在此记录下自己的学习历程。
本篇主要记录关于线性回归的知识(书中是二元线性回归,本文以一元线性回归进行小修改重写便于自身理解)。
- 从零开始的线性回归
- 利用PyTorch简便实现线性回归
- 小结
1.从零开始的线性回归
我们使用一元线性回归模型的真实权重为a=2和偏差b=4,以及一个噪声项c(该噪声项服从均值为0,标准差为0.01的正态分布),随机生成数据集。1.1收集数据集
#获取数据集
import torch
import numpy as np
import random
num_inputs=1
num_examples=1000
true_a=2
true_b=4
features=torch.tensor(np.random.normal(0, 1, (num_examples,num_inputs)), dtype=torch.float)
labels=true_a*features[:,0]+true_b
labels+=torch.tensor(np.random.normal(0, 0.01,size=labels.size()), dtype=torch.float)
其中labels(标签)代表公式里的y,features(特征)代表公式里的x。
1.2读取数据
在训练过程中我们需要不断遍历数据级并分成小批量数据样本进行随机读取。其中小批量数据样本的大小由batch_size(批量大小)来决定。batch_size=10 #批量大小
def data_iter(batch_size, features, labels):
num_examples = len(features)
indices = list(range(num_examples))
random.shuffle(indices) # 样本的读取顺序是随机的
for i in range(0, num_examples, batch_size):
j = torch.LongTensor(indices[i: min(i + batch_size,
num_examples)]) # 最后⼀次可能不⾜⼀个batch
yield features.index_select(0, j), labels.index_select(0,
j)
1.3初始化模型参数
我们将权重a初始化成均值为0、标准差为0.01的正态随机数,偏差b则初始化为0a=torch.tensor(np.random.normal(0,0.01,(num_inputs,1)),dtype=torch.float32)
b=torch.zeros(1,dtype=torch.float32)
#设置允许梯度追踪
a.requires_grad_(requires_grad=True)
b.requires_grad_(requires_grad=True)
1.4定义模型
根据我们的线性回归模型的表达式:
对线性回归的矢量表达式的实现。我们采用torch.mm函数做矩阵相乘
def linreg(x,a,b):
return torch.mm(x,a)+b
1.5定义损失函数
我们需要衡量真实值与预测值之间的误差。通常通常我们会选取⼀个⾮负数作为误差, 且数值越⼩表示误差越⼩。⼀个常⽤的选择是平⽅函数。衡量误差的函数称为损失函数(loss function)。这⾥使⽤的平⽅误差函数也称为平⽅损失(square loss)。def squared_loss(y_hat,y):
return (y_hat-y.view(y_hat.size()))**2/2
1.6定义优化算法
小批量随机梯度下降:先选取⼀组模型参数的初始值,如随机选取;接下来对参数进⾏ 多次迭代,使每次迭代都可能降低损失函数的值。在每次迭代中,先随机均匀采样⼀个由固定数⽬训练数据样本所组成的⼩批量(batch_size),然后求⼩批量中数据样本的平均损失有关模型参数的导数(梯度),最后⽤此结果与预先设定的⼀个正数的乘积作为模型参数在本次迭代的减⼩量。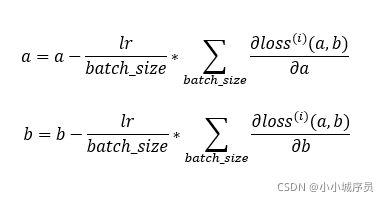
其中batch_size为批量大小,lr为学习率(正数)。这⾥的批量⼤⼩和学习率的值是⼈为设定的,并不是通过模型训练学出的,因此叫作超参数(hyperparameter)。反复调试来寻找合适的超参数可以提高模型的准确率。
def sgd(params,lr,batch_size):
for param in params:
param.data-=lr*param.grad/batch_size
1.7模型训练
在⼀个迭代周期epoch中,我们将完整遍历⼀遍数据集,并对训练数据集中所有样本都使⽤⼀次(假设样本数能够被批量⼤⼩整除)。设置超参数学习率lr=0.03与迭代周期次数num_epochs=5.lr=0.03 #学习率0.03
num_epochs=5 #迭代周期5
net=linreg
loss=squared_loss
for epoch in range(num_epochs):
# 在每⼀个迭代周期中,会使⽤训练数据集中所有样本⼀次(假设样本数能够被批量⼤⼩整除)
for x, y in data_iter(batch_size, features, labels):
l = loss(net(x, a, b), y).sum() # l是有关⼩批量X和y的损失
l.backward() # ⼩批量的损失对模型参数求梯度
sgd([a, b], lr, batch_size) # 使⽤⼩批量随机梯度下降迭代模型参数
#不要忘了梯度清零
a.grad.data.zero_()
b.grad.data.zero_()
train_l = loss(net(features, a, b), labels)
print('epoch %d, loss %f' % (epoch + 1, train_l.mean().item()))
print(a)
print(b)
#结果
#epoch 1, loss 0.000052
#epoch 2, loss 0.000051
#epoch 3, loss 0.000052
#epoch 4, loss 0.000052
#epoch 5, loss 0.000052
#tensor([[2.0006]], requires_grad=True)
#tensor([4.0006], requires_grad=True)
可见,经过5次迭代训练后,训练得到的a=2.0006,b=4.0006,这两者与真实值true_a=2,trye_b=4十分相近。
2.利用PyTorch简便实现线性回归
同理,我们设置一元线性回归的真实权重a=2,偏重b=4,以及一个噪声项c。2.1获取数据集
与1.1同理#获取数据集
import torch
import numpy as np
import random
num_inputs=1
num_examples=1000
true_a=2
true_b=4
features=torch.tensor(np.random.normal(0, 1, (num_examples,num_inputs)), dtype=torch.float)
labels=true_a*features[:,0]+true_b
labels+=torch.tensor(np.random.normal(0, 0.01,size=labels.size()), dtype=torch.float)
2.2读取数据
PyTorch提供了 data 包来读取数据。由于 data 常⽤作变量名,我们将导⼊的 data 模块⽤ Data 代替。在每⼀次迭代中,我们将随机读取包含10个数据样本的⼩批量。import torch.utils.data as Data
batch_size = 10
# 将训练数据的特征和标签组合
dataset = Data.TensorDataset(features, labels)
# 随机读取⼩批量
data_iter = Data.DataLoader(dataset, batch_size, shuffle=True)
2.3定义模型
PyTorch提供了⼤量预定义的层,这使我们只需关注使⽤哪些层来构造模型。⾸先,导⼊ torch.nn 模块。实际上,“nn”是neural networks(神经⽹络)的缩写。顾名思义,该模 块定义了⼤量神经⽹络的层。在实际使⽤中,最常⻅的做法是继承 nn.Module ,撰写⾃⼰的⽹络/层。⼀个 nn.Module 实例应该包含⼀些层以及返回输出的前向传播(forward)⽅法。下⾯先来看看如何⽤ nn.Module 实现⼀个线性回归模型。import torch.nn as nn
class LinearNet(nn.Module):
def __init__(self, n_feature):
super(LinearNet, self).__init__()
self.linear = nn.Linear(n_feature, 1)
# forward 定义前向传播
def forward(self, x):
y = self.linear(x)
return y
net = LinearNet(num_inputs)
2.4初始化模型参数
在使⽤ net 前,我们需要初始化模型参数,如线性回归模型中的权重a和偏差b。PyTorch在 init 模块中提供了多种参数初始化⽅法。这⾥的 init 是 initializer 的缩写形式。我们通过 init.normal_ 将权重参数每个元素初始化为随机采样于均值为0、标准差为0.01的正态分布。偏差会初始化为零。from torch.nn import init
init.normal_(net.linear.weight, mean=0, std=0.01)
init.constant_(net.linear.bias, val=0)
2.5定义损失函数
PyTorch在 nn 模块中提供了各种损失函数,这些损失函数可看作是⼀种特殊的层,PyTorch也将这些损失函数实现为 nn.Module 的⼦类。我们现在使⽤它提供的均⽅误差损失作为模型的损失函数。loss = nn.MSELoss() #均方根误差
2.6定义优化算法
同样,我们也⽆须⾃⼰实现⼩批量随机梯度下降算法。 torch.optim 模块提供了很多常⽤的优化算法⽐如SGD、Adam和RMSProp等。下⾯我们创建⼀个⽤于优化 net 所有参数的优化器实例,并指定学习率为0.03的⼩批量随机梯度下降(SGD)为优化算法。import torch.optim as optim
optimizer = optim.SGD(net.parameters(), lr=0.03)
print(optimizer)
#结果
#SGD (
#Parameter Group 0
# dampening: 0
# lr: 0.03
# momentum: 0
# nesterov: False
# weight_decay: 0
#)
2.7训练模型
我们通过调⽤ optim 实例的 step 函数来迭代模型参数。按照⼩批量随机梯度下降的定义,我们在 step 函数中指明批量⼤⼩,从⽽对批量中样本梯度求平均。num_epochs = 5
for epoch in range(1, num_epochs + 1):
for x, y in data_iter:
output = net(x)
l = loss(output, y.view(-1, 1))
optimizer.zero_grad() # 梯度清零,等价于net.zero_grad()
l.backward()
optimizer.step()
print('epoch %d, loss:%f' % (epoch,l.item()))
print(a)
print(b)
#结果
#epoch 1, loss:0.000197
#epoch 2, loss:0.000067
#epoch 3, loss:0.000173
#epoch 4, loss:0.000168
#epoch 5, loss:0.000099
#tensor([[2.0006]], requires_grad=True)
#tensor([4.0006], requires_grad=True)
可见,经过5次迭代训练后,训练得到的a=2.0006,b=4.0006,这两者与真实值true_a=2,trye_b=4十分相近。
3.小结
- torch.utils.data 模块提供了有关数据处理的⼯具
- torch.nn 模块定义了⼤量神经⽹络的层
- torch.nn.init 模块定义了各种初始化⽅法
- torch.optim 模块提供了模型参数初始化的各种⽅法

