论文《Adaptive Structured Light with Scatter Correction for High-Precision Underwater 3D Measurements》
摘要
高精度水下三维摄像机需要自动化许多传统的水下检查、维护和维修(IMR)操作。:本文介绍了一种新的多频相位步进(结构光)方法,用于在浑浊水中进行高精度的三维估计。介绍了一种自适应相位展开方法,该方法利用相位不确定性来确定可以可靠展开的最高频率。光散射对相位估计有不利影响。提出了一种利用非锐化滤波器消除前向散射效应的方法和一种基于模型的后向散射效应去除方法。在不同浊度下的实验表明,散射校正消除了散射对相位估计的不利影响。与灰度相位步进(GCPS)方法相比,自适应频率解包和散射校正方法具有更高的精度和精度以及更少的相位解包误差。
1.Introduction
传统的水下检查、维护和修理(IMR)操作成本高昂,因为它们需要使用遥控车辆进行手动控制。海底石油工业的一个目标是走向更加自主的IMR作业,这种作业成本效益高,便于在较偏远地区开采石油。为了实现鲁棒和故障安全的自主IMR,需要能够提供高分辨率和高精度的感兴趣对象3D视图的3D传感器。此外,如果三维传感器可以在三维数据上提供“误差条”,自主系统可以做出更可靠的决策,例如,管道是否存在缺陷的可能性,机械手抓取手柄的可靠性,或者水下模板上的阀门是打开还是关闭。
传统上,声纳是水下三维技术的首选,因为它的范围和对水浑浊的鲁棒性。。然而,声呐的图像更新速率受声速的限制,而衍射则限制了横向分辨率。其结果是更新速度慢,三维数据分辨率低,这使得在许多自主的IMR操作中使用它是不现实和不精确的。
如今,摄像机广泛用于遥控潜水器上,作为操作人员的指导工具,也可用于一些自主使用,例如标记[1]。摄像机不像声纳那样受到物理限制。由于光的高速和短波长,相机允许快速采样率和高横向分辨率。但在实际应用中,光与水的相互作用会引起光的衰减和散射,影响光学三维系统的性能。:衰减和散射的效果取决于水的浑浊度。光的衰减限制了系统的势范围,而散射主要有两个影响。后向散射导致图像对比度下降,而前向散射导致特征模糊。消除二维图像散射效应的一些典型方法是应用图像去噪[2,3]、去卷积[4]或特定的正向或反向散射模型[5,6]。
单摄像机系统能够通过摄影测量[7]提取三维信息。立体视觉作为一种三维传感技术得到了广泛的应用,主要是因为其结构相对简单、造价低廉。一个立体相机系统由两个标定的相机和一个立体匹配算法组成,该算法根据相机[9]中相应的极线搜索相应的特征。一旦建立了对应(视差),就可以通过简单的三角法来估计距离。一旦建立了对应(视差),就可以通过简单的三角法来估计距离。由于衰减和散射会降低图像对比度、分色和抹去图像特征,因此在水下图像中建立特征对应关系具有挑战性[5]。此外,许多水下结构是无纹理的,这使得几乎不可能找到特征对应。
水下常用532纳米激光器作为光源,通过减小光的衰减和散射效应来增大成像范围。三角测量系统投射激光,通常为激光片[10 - 12]或点[13],通常包含相对较慢的扫描机制,以覆盖扩展的视野。:在较短的距离内,由于高能量聚焦光,成像传感器很容易饱和。另一种更快的方法是用短而强大的光脉冲照亮整个视野,并使用快速距离门控相机估计飞行时间[14-16]。距离门控解是抑制后向散射的有效解[15,17]。结构光传感器通常使用DMD实现空间编码光的快速时间复用[18]。与基于激光的海底干预和检查扫描方法相比,其优势在于在0.5 m-2 m范围内具有实时帧率和横向和深度分辨率的潜力。典型的模式有二进制[18]、灰度编码[19]或正弦条纹模式[20]。在高频移相正弦波[21]中,常采用灰度编码对相图进行相位解包。这种系统的深度精度受能够可靠分割[22]的码数的限制。随着浑浊度的增加,受照区域和非受照区域的边界变得模糊,很难进行准确的[23]分割。
采用多频移相投影(MFPS),根据剩余定理[24]或相位不确定性[25]对相位进行解包,可以替代使用二进制/灰度编码进行相位解包。本文提出了一种适用于水下应用的MFPS方法的水下结构光系统。光在水中的正向散射可以看作是与对称点扩散函数(PSF)的卷积。在理想情况下,对称PSF与无限正弦波的卷积不会改变相位或频率,只会改变振幅。不幸的是,投影的正弦波是有界的,高差会改变正弦波模式,使其不是从相机上看到的空间正弦信号。因此,散射影响了正弦条纹图的相位估计。我们提出了消除后向散射和前向散射影响的模型。建立了信号的噪声与相位估计的关系。相位不确定性是用来展开高频相位估计的。结果得到了一个深度不确定的密集深度图。我们将结果与GCPS进行比较。
2. Material and Methods
在本节中,我们首先介绍了用于生成本文结果的硬件。尽管相位步进和相位展开的深度精度概念已在其他地方发布,但我们在第2.2和2.3节中对它们进行了简短的总结,以介绍我们的符号。第2.4和2.5节总结了我们提出的自适应相位展开和散射去除方法。
2.1 Underworter Housing and Sensor
该结构光传感器由机器视觉摄像机和DMD(数字镜像设备)投影仪组成(见图1a)。投影仪是一个LightCrafter RGB投影仪(DLP®LightCrafter™)(美国德克萨斯州达拉斯市德州仪器公司4500),可方便地显示120hz 8位模式。:机器视觉相机为BU238M USB 3.0黑白相机(东芝,东京,日本),分辨率1920×1200。摄像机以4倍的增益运行,导致数字到光电转换系数γ=33。我们只使用投影仪的绿色LED,以避免在空气到水的过渡色差。光谱的绿色部分在水中也是衰减最小的。
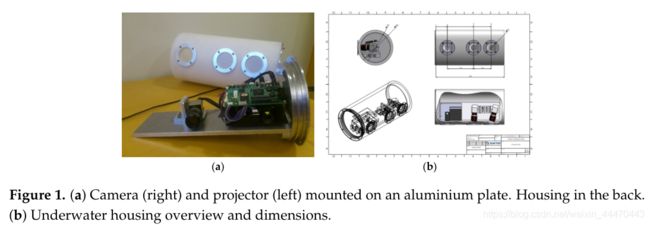
水下外壳,如图1b所示,由一个圆柱形塑料外壳组成,带有摄像头和投影仪的窗户。外壳装有三个窗户,以便于调整基线。较长的基线对于需要较长的成像距离的用例可能更好,而较短的基线对于较短的成像距离是足够的。摄像机和投影仪安装在金属板上,金属板与其中一个端板相连。端面板拧在钢瓶上,用一组双o形环密封。一个10米长的软管连接到外壳上。我们目前使用的USB 3.0摄像头不支持超过10米长的电缆,但是,如果使用千兆以太网摄像头,我们可以将电缆延长到100米,如果用例允许的话。
2.2 Depth-Precision of Phase Stepping
相位步进深度估计程序包括捕获投影到场景上的三个或更多相移正弦图像,并测量每个像素的相移。本文主要研究了四步相移正弦信号的情况,其中通过[21]可以估计出未包绕的相移:

投影的正弦曲线在i1,…, I 4是相移与90◦相对于其他的。图像由信号电平(振幅)表示 I a ( x , y ) = ( I 1 ( x , y ) − I 3 ( x , y ) ) 2 + ( I 2 ( x , y ) − I 4 ( x , y ) ) 2 I_a(x,y)=\sqrt{(I_1(x,y)-I_3(x,y))^{2}+(I_2(x,y)-I_4(x,y))^{2}} Ia(x,y)=(I1(x,y)−I3(x,y))2+(I2(x,y)−I4(x,y))2和背景信号电平 I b ( x , y ) = 1 4 ∑ i = 1 4 − I a ( x , y ) / 2 I_b(x,y)={\frac{1}{4}}{\sum_{i=1}^{4}}-I_a(x,y)/2 Ib(x,y)=41∑i=14−Ia(x,y)/2以光电的单位来测量。总信号确定为 I s = I a + I b I_s=I_a+I_b Is=Ia+Ib。相位不确定度取决于图像噪声,主要是每个相移图像的拍摄噪声,可以显示为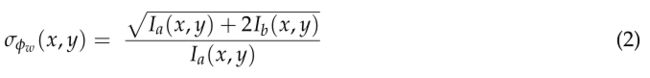
2.3 Phase Unwarpping
对于超过一个周期的正弦波,在(1)中的相位估计将被包裹在2π处。要生成未展开的相位估计:

我们需要找到P (x,y)它决定了一个像素所处的正弦周期在投影的 N P N_P NP个周期中。展开相位的像素标准差为:
估计P (x,y)为不止一个频率模式的标准方法是使用灰色代码[21]。为了估计一个n位的灰度编码,需要投影n+2幅图像。 I s , I b 和 I G 1 , . . . , I G n I_s,I_b和I_{G_1},...,I_{G_n} Is,Ib和IG1,...,IGn。在此基础上对灰度编码进行估计 G i = 1 2 I a + I b < I G 。 G_i={\frac{1}{2}}I_a+I_b<I_G。 Gi=21Ia+Ib<IG。在以镜头噪声为主要噪声贡献的情况下,黑色像素和信号像素的噪声为 σ b = I b \sigma_b=\sqrt{I_b} σb=Ib和 σ s = I a + I b \sigma_s=\sqrt{I_a+I_b} σs=Ia+Ib。在图2中,我们展示了在不同信号水平下模拟灰度代码分割的结果。误码率随总强度 I s I_s Is和背景与信号之间的强度分布而变化。大多数场景的对象具有不同的反照率,因此也有不同的 I a I_a Ia和 I b I_b Ib级信号。其结果是,在场景的某些区域,信号电平较低,灰度解码的错误率较高,导致像素相位展开错误。这是一个特别的问题,在水下,过渡将被涂抹的空间,因为正向散射,即, I a I_a Ia在过渡点附近会比远处低,而 I b I_b Ib可能由于后向散射而升高。相位展开的灰度编码方法在为像素选择合适的周期时没有考虑信号的电平和信号的不确定性,使其成为一种不灵活的方法。
2.4 Adaptive Multi_Frequency Phase Stepping
在本节中,我们将介绍一种灵活的相位展开方法,它是由数据驱动的。根据式(4),相位步进具有更高的频率正弦波形,具有更高的深度精度。然而,主要的问题是在不同的信号电平下准确地解相位。该方法利用像素级的信号电平和相关的信号不确定性来确定最高的正弦频率,该频率可以相位展开而不产生歧义。
假设我们已经预测了一个周期的正弦模式 φ 1 φ^1 φ1和一个n-周期的正弦模式 φ w n φ_w^n φwn。传统的(MFPS)相位展开方法 φ w n φ^n_w φwn用于解决:![]()
由于 φ w n ( x , y ) φ^n_w(x,y) φwn(x,y)的不确定性,n值越高,在进行相位展开时的误差率越高。我们提出了一种数据驱动的MFPS展开方法,该方法基于信号的不确定性决定了一个n个像素能跳到多高的程度。
我们可以从误差率小于 γ σ φ γσ_φ γσφ的基频对像素进行相位展开的最大周期数,其中 γ γ γ是一个参数,由跳跃因子确定:
因为这是一个像素级的因素,每个场景都不一样,所以实时改变投影模式的频率是不现实的。在实际应用中,提出了一种预先定义的正弦频率计划,并根据像素跳变因子将像素逐相位展开到允许的最高频率。值得注意的是如果一个像素可以从基准周期跳转到因子2,那么它也可以从任何已分阶段展开的较高周期跳转到因子2。
确定频率计划是在帧速率(频率越高,需要投影的图案数量越多,所需时间越长)、潜在精度(频率越高,潜在精度就越高)随着跳频的增大,相位错误展开的几率增大。在本文中,我们建议使用如下频率表:1、8和64。这导致了12个投影模式,这与64频信号的灰度码相位步进(GCPS)方法所需的模式相同(4个移相的64频正弦信号,一个完全照亮的非照亮图像,以及6个编码灰度码的图像)。假设频率之间的跳转因子相同(为8),我们将尽可能多的像素跳转到64的可能性最大化,并将相位展开的可能性最小化。与灰度编码相比,相位估计的优点是相对于信号电平具有自适应能力。相位估计将具有可预测的下限相位精度(不确定性),相位展开的错误率较低,与信号电平无关。相位精度是一个较低的界限,因为它将镜头噪声作为唯一的噪声贡献,而忽略了其他噪声源,如浑浊度。
2.5 Scatter Removal(散射校正)
混浊介质中的光散射通常以两种方式影响有源照明成像系统。光的后向散射增加了背景水平,而前向散射模糊了图像特征。在本节中,我们描述了这两种方法对投影图像的影响,并提出了在应用MFPS算法之前消除散射效应的算法。我们提出通过从原始图像中减去一个与浊度相关的后向散射模型来去除后向散射,而采用非锐化滤波器来去除前向散射。结果部分显示了散射消除对相位估计的影响。
2.5.1 Backward Scatter Removal
后向散射剖面是一个复杂的体积函数,它取决于光照体积、水的衰减和水的角相关散射截面。在MFPS中,每个被投影的连续正弦图形的光照体积都会发生变化,这使得通过参数函数来逼近这个函数非常困难。相反,我们对每个MFPS模式在不同浑浊度下的后向散射剖面进行成像。这是在一个水族馆(125厘米×50厘米×50厘米)中进行的,在那里通过向水中添加粘土来改变浑浊度。水族馆的内墙上覆盖着黑色的织物,以确保所有返回的光线都来自于背向散射。浊度(衰减长度)的测量方法见附录B。
图3显示了1和4周期正弦图在高浊度下不同位移正弦曲线的后向散射剖面。像素的后向散射随投影正弦信号的频率f、正弦信号的相移p(1到4)和浊度的变化而变化。假设我们知道将使用的频率和相移,我们建立了一个后向散射模型,通过投影和成像正弦与上述频率和相位在预先确定的浊度。基于采样的后向散射图像,构造了三维后向散射体 B f p ( x , y , t ) B_f^p(x,y,t) Bfp(x,y,t),其中前两个维定义图像像素,第三维参数化浑浊度。后向散射模型沿浊度维插值,以方便在原始采样浊度范围内的任意浊度。在本文中,我们在四个混浊/衰减长度,即0.8米、1.1米、2.0米、5.8米。假设我们在浑浊度t处投影一个相位为p,频率为f的正弦信号,原始采样图像包括后向散射为 I p f ( x , y ) I^f_p(x,y) Ipf(x,y)。简单地从原始图像中减去后向散射如下: I p ′ f ( x , y ) = I p f ( x , y ) − B p f ( x , y , t ) I'^f_p(x,y)=I^f_p(x,y)-B^f_p(x,y,t) Ip′f(x,y)=Ipf(x,y)−Bpf(x,y,t)。该模型假设后向散射与场景中物体的距离无关。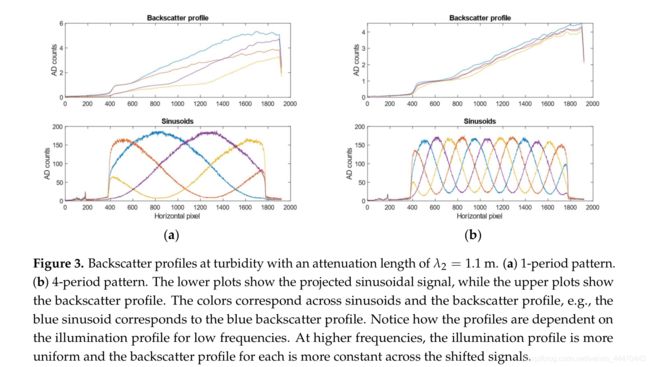
2.5.2 Forward Scatter Removal
前向散射导致特征模糊。图4显示了前向散射psf的捕获范围,它随着浊度的增加而增大,甚至在高浊度时影响到图像边界上的像素。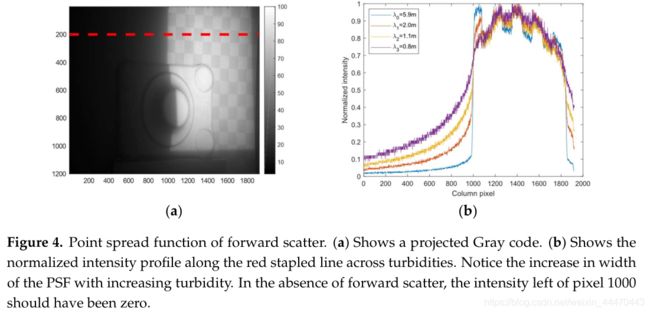
PSF的宽度也取决于到场景的距离。完美正弦波和对称核之间的卷积不会改变信号的相位或频率,只会改变信号的振幅。但是,由于PSF太宽,图形的边界会影响远离边界的正弦波,改变其相位。此外,当正弦信号反射到具有深度差异的场景后,由于相位偏移,反射后的图像将不再是空间正弦信号,PSF将改变图像的相位/频率。
前向散射消除的一种方法是对PSF进行建模,并使用去卷积算法消除前向散射效应。从图4看,参数函数能否准确地逼近PSF并不明显。此外,由于混浊度的微小变化,PSF可能在图像上有所变化,并且由于混浊度和拍摄噪声,图像可能会有噪声。所有这些因素都使得去卷积算法的设计变得困难。相反,我们建议使用一种对宽的空间变化的PSF和噪声更为稳健的非锐化滤波方法。
非锐化滤波方法从原始图像中减去低通滤波后的图像,增强高频内容:
内核k是一个低通高斯,由像素宽度w和标准偏差 σ 1 \sigma_1 σ1定义。减法量表 θ t \theta_t θt和重新调整量表 ρ t \rho_t ρt取决于浑浊度。图5显示了在图4所示的信号上使用这里描述的非锐化滤波技术进行前向散射调整的结果。该方法减少了PSF对图像左边界的影响,同时保留了像素1000到1800之间的强度特征。在本文中,手动调整比例因子。然而,当将该算法应用于单周期正弦模式时,可以通过找到最高的散射因子来自动估计它们,该因子不会导致任何负值像素。
3. Result
所有测试数据均在控制浑浊度的水族馆中获得。在本节中,我们总结了测试设置和数据采集,然后评估了散射校正的性能,并比较了与GCPS算法相关的自适应MFP。使用附录A中概述的简单校准程序,使用L=80 cm、B=15 cm和比例常数6.5进行相位到距离的转换。
3.1 Test Setup and Data Acquisition
实验采用尺寸为125 cm×50 cm×50 cm的水族箱,如图6所示。相机被放置在水族馆外面。水族馆里装满了自来水。首先,我们获取了放置在鱼缸内距摄像机80 cm处的白色哑光板的数据,并将其作为校准程序的参考平面,如附录a所示。获取参考平面后,我们将其更改为如图6所示的板,其中一半为哑光白色,另一半为棋盘格图案(深色方块的反照率为0.5)。这是为了测试不同反照率对算法的影响。接下来,一个高度为11厘米的物体被放置在盘子前面。我们获得的数据的这一幕清晰的自来水(λ0 = 5.9 m)和在其他三浊度水平(λ1 = 2.0米,λ2 = 1.1米,λ3 = 0.8米)。将黏土依次加入水中,增加浑浊度。浊度的测定方法见附录B.在每个浊度水平下,我们得到以下数据:
- GCPS数据。我们使用了6个灰度码模式,1个黑白图像和4个相移64周期正弦曲线共12幅图像。
- 自适应mfps数据。我们用4个频率分别为1、8和64的相移正弦波共12幅图像。

图7显示了获取的数据集的图像。图像显示一个频率为8的正弦信号在不同的浊度水平。

3.2 Effect of Scattering on Phase Estimates
光在水中的散射影响相位估计。在图8中,我们展示了正向和反向散射对相位估计的综合影响。一个频率分量的相位偏差远大于八个频率分量。散点PSF具有较宽的范围,其边界影响到远至图像中央的正弦波,如图8a所示。这种影响在图8d中并不明显,因为由于较高的频率信号,边界效应得到更快的缓解。背景信号( I b I_b Ib)从左到右的增加如图8b,e所示,表明中/右像素的后向散射比左像素的后向散射更明显。这可以用相机与投影仪光线的角度相关截面来解释。

3.3 Backscatter Compensation
如图3所示,后向散射对正弦分量的影响不同。在图9中,我们将估计的后向散射贡献添加到理想的相移正弦,以增加浑浊度,并估计与地面真值相关的相位差。最高浑浊度时的最大相位偏差达到0.2弧度,我们可以用后向散射补偿来调整。对于高周期模式,效果并不突出,因为在这种情况下,沿相机光线的照明轮廓积分将跨越多个周期,图像上的后向散射信号将均匀。使用方程式(a1)中的简化校准公式,基线为15cm,距离目标为80cm,比例常数为6.5,0.2弧度误差等于约6.9cm的公制误差。修正由后向散射引起的这种偏差可以提高不能跳到高频正弦的低信噪比像素的精度。这种偏差对低频正弦最为显著,这意味着相位相对于高频正弦发生了偏移。如果这种影响没有得到纠正,在极端情况下,从低频跳到高频时,相位展开可能会出现系统误差。
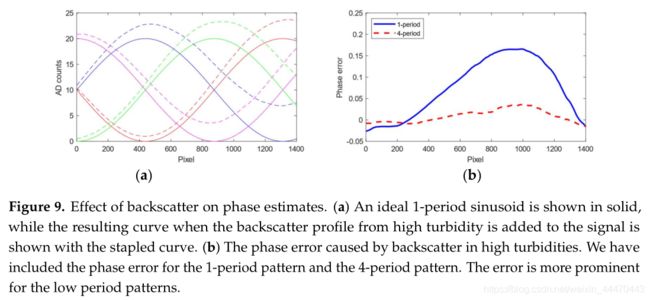
图10中显示的结果后向散射校正后的浊度λ3 = 0.8 m的数据集在图7中。我们只显示了单周期模式的效果,因为这是后向散射效果最强的地方,如图3所示。对相位的影响与仿真结果如图9所示,即,后向散射校正图中右侧的相位差。

3.4 Forward Scatter Compensation
图10显示了前向散射消除对图7中数据集第200行的后向散射消除强度分布的影响,其中λ2=1.1 m。我们使用了θ=0.5和ρ=1.4的比例因子,以及W=1000和σi=800的高斯低通滤波器。我们可以看到,在(d)中的散射校正之后的分量交叉(例如,紫色和橙色曲线在像素300附近交叉的位置)比在(b)中更符合(a)中的分量交叉。对相位估计的影响可以在(e)中看到,其中,除了边界处,对λ0处相位的偏差进行了很大程度的修正。
3.5 MFPS versus GPCS
在图11中,我们显示了经过散射校正的GCPS和MFPS之间的比较结果。即使在相对清澈的水中(λ1),GCPS的相位展开也会产生误差。这从GCPS相图中沿垂直平行条纹的误差可以明显看出。注意,对于GCPS方法,浑浊度增加沿灰度编码边界的误差,而对于MFPS方法,浑浊度的增加增加板边界的误差,而MFPS方法没有进行散射校正。这与图10中所示的分散效果一致。提出的散射校正算法消除了大部分边界效应。
在表1中,我们显示了基于图11中所示区域的定性结果。误差估计值被视为图11所示的与地面真值的距离大于 ± 2 π 64 \pm{\frac{2\pi}{64}} ±642π的整个区域中像素的百分比。这将指示被错误地相位展开的像素数。误差,即误差的精度和精度,估计在图11所示区域中间的100×100区域。最后一列用式(4)表示预测相位标准差,结果表明预测相位是MFPS算法的下界,主要是因为它只考虑拍摄噪声。在低浑浊度下,由于引起浑浊度的颗粒对单个相图增加了相当大的噪声,因此它是一个较好的预测器。散射校正的MFPS算法包含更少的误差,并提供了一个显着提高精度和精度跨越浊度。

MFPS算法分多个阶段展开相位。在本文中,我们使用了频率表1、8和64。在表2中,我们给出了在混浊度λ2=1.1 m下每一相的定量结果。这些结果表明,仅使用1或8个频率即可实现性能。我们发现相位不确定性允许所有像素执行8的频率跳跃。在低浑浊度时,信号允许大部分像素直接从基频跳到64。

在图12中,我们显示了来自图7中对象成像的定性结果。我们将提出的散射校正后的MFPS结果与使用GCPS的结果进行了比较。这些图像支持定量结果:散射校正后的MFPS具有显著的更少的异常值,更高的精度和精度,并随着浊度的增加降解更好。

4. Discussion
介绍了一种用于浊水中高精度水深测量的结构光法。该方法基于MFPS相位展开方法,但包含了相位/距离不确定性的可预测下限,用于确定可展开的最高可靠频率。此外,研究了散射对相位估计的影响,提出了减小散射对相位估计影响的方法。结果表明,该方法能提供更准确、更精确的水深估计,并能较好地降低浑浊度,具有更好的可预测性。
对于这里提供的示例,像素级的不确定性足够低,能够根据所使用的频率调度(即1、8、64)跳跃。然而,我们仍然观察到像素被错误地展开。这可以用几个因素来解释。首先,不确定性只是一个下限,因为它只依赖于镜头噪声。除散粒噪声外,浊度是导致相位不确定度增加的主要因素。随着混浊度的增加,水中存在和移动的颗粒越来越多,因此像素级的散射效应可能不同于暴露的情况,从而增加测量的噪声。然而,这种影响很难参数化,而量化这种噪声的稳健方法将是未来工作的一部分。如果镜头噪声是实现频率跳变的限制因素,那么降低噪声的一种方法是自适应地丢弃像素。如果我们通过3×3像素的组合将镜头噪声降低3倍,那么跳频因子也会增加同样的因子。
在本文中,我们对每个频率使用三个频率和四个相移正弦来进行距离测量。因此,采集了12幅图像来进行距离测量,使用当前系统大约需要100毫秒。在相机或场景正在移动的动态情况下,这可能太长,无法避免运动人工制品。一种解决方案可以是以较高的相位不确定性为代价仅使用三相移正弦波,或者减少频率调度以仅包含基频和较高的频率。频率越高,如果相位不确定性允许展开信号,则距离估计将越精确。如果仅使用基频,则要求的最小曝光次数为3次,如果还使用另一个更高的频率,则要求的最小曝光次数为6次。如果需要高精度估计和非常可靠的相位展开,可以使用更多的频率。
后向散射主要影响低频和最右边的像素。这是因为与右侧像素对应的相机光线在击中目标之前会穿过整个投影仪的照度。因此,对于低频信号,不同的偏移正弦信号,背散射光也会不同。对于高频信号,这种效应会抵消,因为摄像机的光线会穿过投影信号的多个峰值。前向散射是由与投影信号卷积的大PSF引起的。边界效应是我们观察到的相位偏差的主要原因。即使在高混浊度下,非锐化滤波器也能调节大部分前向散射效应。
我们将所提出的方法与无误差修正的标准gcps方法进行了比较。与本文报道的结果相比,使用灰色码的纠错可以在一定程度上改善GCPS结果。我们发现,由于消除了散射效应,mfps可以提供更精确的结果,并且包含更少的相位展开误差。gcp和mfp的结果使用相同数量的模式计算。当gcps速度快且仅依赖于逐像素计算时,散射校正mfps速度慢,因为它需要在非锐化滤波过程中应用大型卷积滤波器,并且方程(5)的解不像计算灰度代码那样简单。在运行非优化代码的Matlab的标准笔记本电脑上,灰色代码法在0.6s内运行,标准MFPS在2.6s内运行,而前向散射消除滤波器在9s内运行,但是我们相信,在GPU上巧妙的实现可以大大减少这一差距。
Appendix A. Calibration
基于空气的结构光系统基本上可以用与传统立体系统[26]类似的方法进行校准。然而,由于空气-水的折射作用,针孔相机模型在水中的有效性受到质疑,需要更复杂的模型来建立精确的校准模型[27]。由于本文的重点是准确估计散射介质中相移的方法,因此我们使用了一种简化的校准方法[28],它提供了一个公制距离图,而不是欧几里得点云。然而,任何为水下结构光系统设计的校准都可以将相位图转换为欧几里德点云。
假设我们有一个摄像机投影仪基线B和一个到参考平面的距离L,如图A1所示。利用简单的三角学,我们发现以下关系:
Z L − Z = d B \frac{Z}{L-Z}=\frac{d}{B} L−ZZ=Bd,或 Z = L − Z B d Z=\frac{L-Z}{B}d Z=BL−Zd,其中z是参考平面的高度。简化关系可推导出:
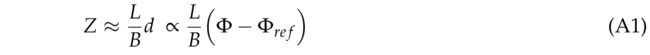
我们用估计的相移 ϕ − ϕ r e f \phi-\phi_{ref} ϕ−ϕref来交换距离偏移d。
Appendix B. Attenuation Measurement
光在水中的衰减由 I Z = I 0 e − z / λ I_Z=I_0e^{-z/\lambda} IZ=I0e−z/λ中的衰减系数k决定。其中 I 0 I_0 I0和 I z I_z Iz是距离为0和z处光源的强度。直接测量 I 0 I_0 I0是困难的,所以我们测量不同距离的对数强度,并找到零点交叉,这是对 I 0 I_0 I0的估计。因此,通过在距离z处测量一个新的浊度的 I z I_z Iz,我们可以通过 λ = − z l n I z I 0 \lambda=-\frac{z}{ln\frac{I_z}{I_0}} λ=−lnI0Izz确定衰减系数。