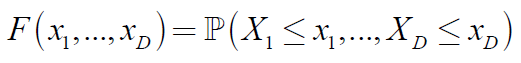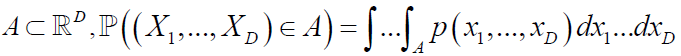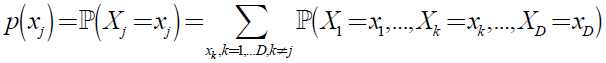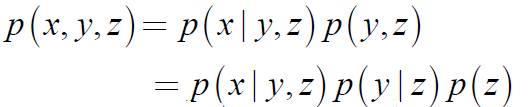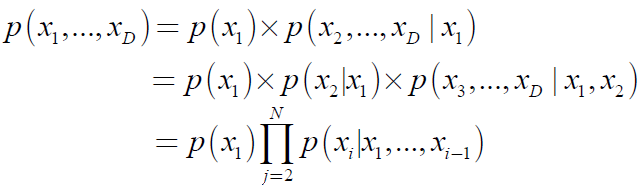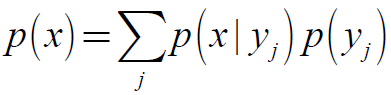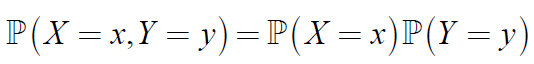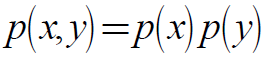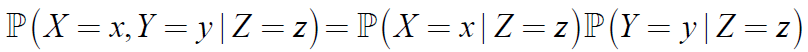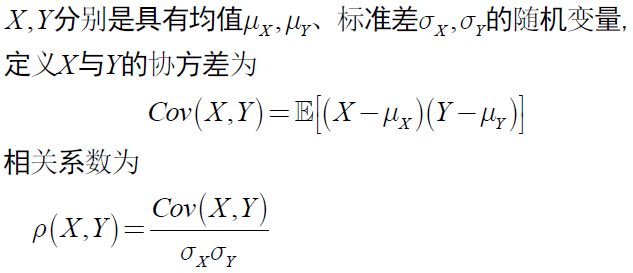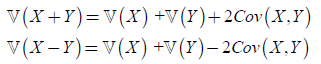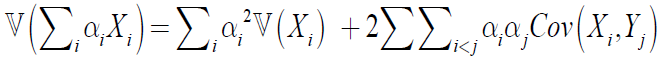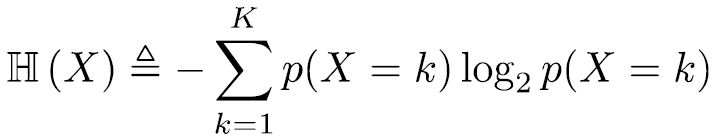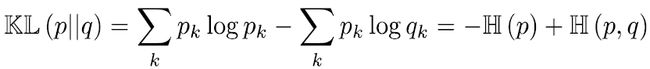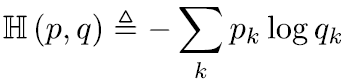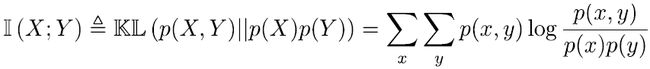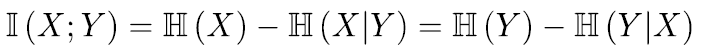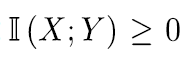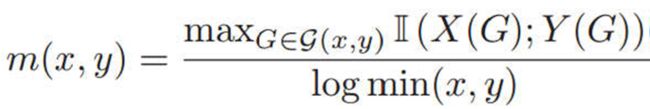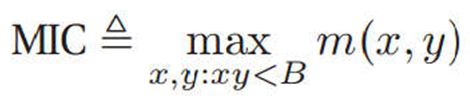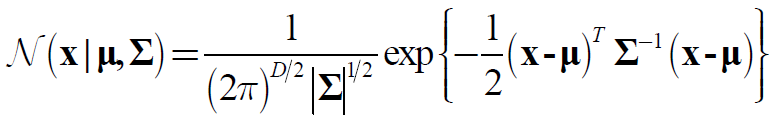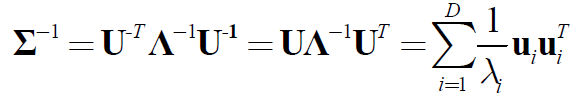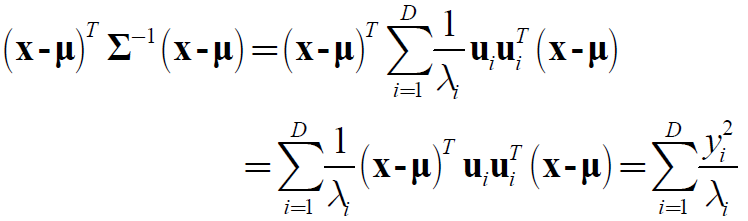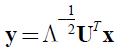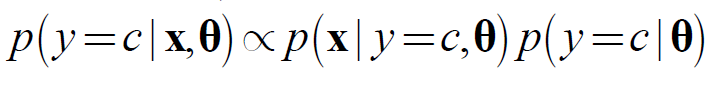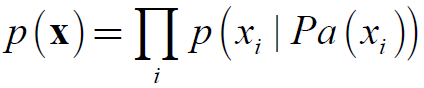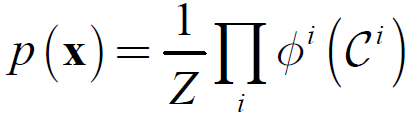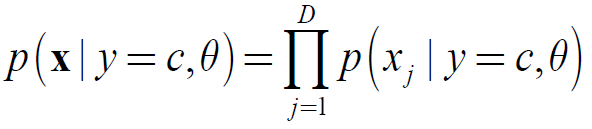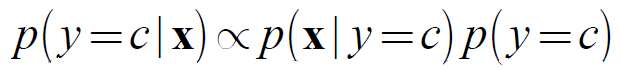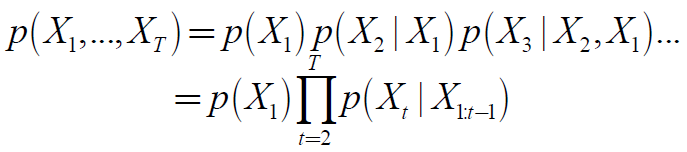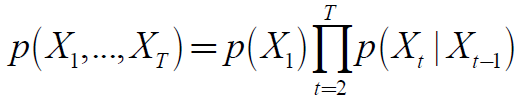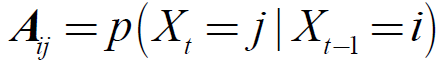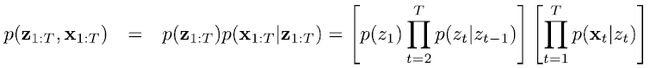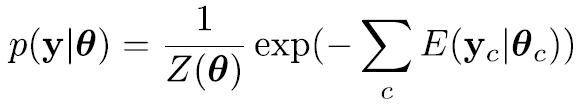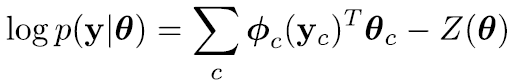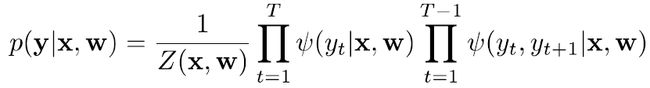目录
一、 随机向量及其分布... 2
1.多元向量的联合分布... 2
1.1离散情况... 2
1.2连续情况... 2
2.多元向量的边缘分布... 2
2.1离散情况... 2
2.2连续情况... 2
3.多元向量的条件分布... 2
4.贝叶斯规则... 3
5.多元向量独立... 3
6.多元向量条件独立... 3
7.协方差与相关系数... 3
8.方差-协方差矩阵... 4
9.信息论... 4
9.1机器学习原则... 4
9.2熵... 4
9.3 KL散度(Kullback-Leibler divergenc,KL divergence)... 5
9.4互信息... 5
9.5最大信息系数(maximal information coefficient,MIC)... 5
二、多元正态分布... 6
1.多元正态分布(multivariate normal, MVN)... 6
2.协方差的特征值分解... 6
3.MVN的白化... 6
4.高斯判别分析(GDA)... 6
5.决策边界... 6
三、概率图模型... 7
1.有向图... 7
2.无向图... 7
3.特殊的概率图模型... 7
3.1朴素贝叶斯分类器(Naive Bayes Classifier, NBC)... 7
3.2链规则... 7
3.3 Markov链... 7
3.4转移矩阵... 8
3.5隐马尔科夫模型(HMM)... 8
3.6 Markov随机场(MRF)... 8
3.7 条件随机场(CRF)... 9
一、随机向量及其分布
多元随机向量的分布:在多个随机变量组成的向量上定义的分布。
1.多元向量的联合分布
1.1离散情况
假设D维随机向量(X1, …, XD),其中Xj为离散型随机变量,则定义联合概率质量函数(pmf)为:
联合概率分布函数(CDF)为:
1.2连续情况
假设D维随机向量(X1, …, XD),其中Xj为连续型随机变量,则定义联合概率密度函数(pdf)为:
其中:
联合概率分布函数(CDF)为:
对任意集合:
2.多元向量的边缘分布
2.1离散情况
假设D维离散型随机向量(X1, …, XD)有联合质量函数p(X1, …, XD),则定义Xj的边缘概率质量函数:
2.2连续情况
假设D维连续型随机向量(X1, …, XD)有联合质量函数p(X1, …, XD),则定义Xj的边缘概率质量函数:
3.多元向量的条件分布
(1) 例如,对二维随机变量(X,Y), 当p(y) > 0时,给定Y=y时X的条件分布为:
即:
(2) 链规则(Chain Rule)
例如有3个随机变量时:
或者:
一般地,
4.贝叶斯规则
(1) 全概率公式
如果Y可以取值y1, …, yK,x为X的一个取值,则:
(2) 贝叶斯规则:
5.多元向量独立
若对向量中X,Y中所有的x, y,有:
或者:
则称X与Y独立,记作:X⊥Y
6.多元向量条件独立
若对向量中X,Y,Z中所有的x, y, z,有:
或者
则称X与Y条件独立(即有条件的独立),记作:X⊥Y | Z
7.协方差与相关系数
如果随机变量之间不独立,可用协方差/相关系数来刻画两个随机变量之间关系强弱:
性质:
(1)
协方差满足:
相关系数满足:
(2) 如果X,Y独立,则:
(3) 协方差:
对任意两个随机变量X和Y,有:
推广到多个随机变量:
8.方差-协方差矩阵
令随机向量X的形式为:X = (X1, …, XD)T,则方差-协方差矩阵定义为:
当各个成分变量独立时,协方差矩阵是一个对角矩阵。
9.信息论
9.1 机器学习原则
(1)选择最简单的、能表示数据产生规律的模型
(2)模型选择:最小描述长度准则
(3)特征选择:选择与目标最相关的特征
9.2 熵
(1)熵是一种不确定度的度量
(2)定义:
假设随机变量X的分布为p,则该随机变量的熵定义为:
9.3 KL散度(Kullback-Leibler divergenc,KL divergence)
KL散度,又称相对熵(relative entropy):一种度量两个分布p和q之间的差异的方法:
或者:
其中H(p, q)称为交叉熵:
9.4互信息
互信息:度量联合分布p(X, Y)和因式分解形式p(X)P( Y)之间的相似度:
或者:
其中H(X|Y)或H(Y|X)称为条件熵(表示观测到X后Y的不确定性减少):
性质:
(1)互信息不小于0:
(2)当且仅当p(X, Y)= p(X)P( Y),即X 与Y独立时,互信息为0.
(3)在特征选择时,可以通过计算特征与目标之间的互信息,选择与目标互信息最大的那些特征,抛弃与目标关系不大的特征。
9.5最大信息系数(maximal information coefficient,MIC)
(1)连续变量的互信息,需先离散化,再计算互信息。
(2)最大信息系数(MIC):以最优的方式离散化,并将互信息取值转换成到[0,1]:
其中I(X(G);Y(G))为某种离散方式, 箱子大小B建议为N0.6,N为样本数目。
二、多元正态分布
1. 多元正态分布(multivariate normal, MVN)
多元正太分布的一般形式 :
其中,
期望:μ=E(x) , 协方差矩阵:Ʃ = E( (x-μ)T(x-μ) ),即可以写成方差-协方差矩阵的形式。
协方差矩阵有D x (D-1)/2个独立元素,是正定矩阵,
协方差矩阵的逆 = 精度
2. 协方差的特征值分解
协方差矩阵的特征值分解:
则Mahalanobis 距离(等于在翻转坐标系中的欧氏距离):
其中,yi = uiT (x -μ)
3. MVN的白化
假设x随机向量服从多元正态分布:
则令y的分布为:
称y已经被白化了,即已经服从了标准正态分布:N(0,I)
4. 高斯判别分析(GDA)
在产生式分类器中:
使用高斯分布作为类条件分布:
通过分析这个高斯分布来确定最佳的分布的方法,叫高斯判别分析(GDA)。
例如,当协方差矩阵为对角阵时,为朴素贝叶斯分类器(各特征独立)。
5. 决策边界
(1) 当所有都相等时,判别边界为线性,称为线性判别分析(Linear Discriminant Analysis, LDA)
(2) 一般情况下,判别边界为二次曲线
(3) 协方差决定了模型的复杂度(参数的数目)
三、概率图模型
利用随机变量之间的条件独立关系,可以将随机向量的联合分布分解为一些因式的乘积,得到简洁的概率表示。
1.有向图
有向图模型(directed graphical models,DGMs)使用带有有向边的图,用条件概率分布来表示分解:每个随机变量xi都包含着一个影响因子,这些影响因子被称为xi的父节点,记为Pa (xi),则有向图模型表示概率分解:
2.无向图
无向图模型(undirected graphical model,UGM):使用带有无向边的图,将联合概率分解成一组函数的乘积。
图中任何满足两两之间有边连接的顶点的集合被称为团(clip),每个团Ci都伴随着一个因子: ɸi(Ci), 并且这些团必须满足:
(1)每个因子的输出都必须是非负的
(2)但不像概率分布中那样要求因子的和/积分为1
则随机向量的联合概率可以分解为:所有这些因子的乘积:
其中归一化常数Z被定义为函数乘积的所有状态的求和或积分,使得这些乘积的求和为1(即使得p(x)为一个合法的概率分布)。
3.特殊的概率图模型
3.1 朴素贝叶斯分类器(Naive Bayes Classifier, NBC)
(1)原理:假设各维特征在给定类别标签的情况下是条件独立的。
(2)假设要进行分类,共有C个类别y∈ (1,2,…, C),每个样本有特征x = (x1, …, xD),则给定类别标签下的条件概率为:
(3)进行分类(预测):
3.2链规则
给定时间长度为T 的序列X1,…, XT,则链规则:
即第t时刻的状态Xt只与前t-1个时刻的状态X1:t-1相关。
3.3 Markov链
假设第t时刻的状态Xt只与前一个时刻的状态Xt-1相关,称为一阶Markov假设,得到的联合分布为Markov链(或Markov模型):
3.4转移矩阵
当Xt∈(1,2,…,k)为离散时,则条件分布p(Xt|Xt-1)可表示为一个K x K的矩阵|Aij|,称为转移矩阵,其中:
表示从状态i转移到状态j的概率,也称为叫做随机矩阵。
3.5隐马尔科夫模型(HMM)
如果系统的状态不可见,只能观测到由隐含状态驱动的观测变量,则可用隐马尔可夫模型(Hidden Markov Model, HMM)表示联合概率:
其中:
其中zt表示第t时刻的隐含状态;
p(Zt|Zt-1)表示转移模型;
p(Xt|Zt)表示观测模型。
3.6 Markov随机场(MRF)
(1)定义
随机场可以看成是一组随机变量的集合(这些随机变量之间可能有依赖关系);
Markov随机场:加了Markov性质限制的随机场,可用无向图表示。
(2)MRF的参数化
1)
无向图中节点之间的边没有方向,不能用链规则表示联合概率,而是用图中每个最大团C 的因子的乘积表示:
其中Z为归一化常数。
2)
或者,使用能量函数表示为:
其中E(yc)为团簇C中变量相关的能量函数。
3)
或者,将log势能函数表示为一些函数的线性组合:
其中,组合权重为Ɵ,ɸc为根据变量yc得到的特征。
则log联合分布表示为:
称为最大熵模型或log线性模型,在条件随机场(CRF)、(受限)Boltzmann机(RBM)可用此形
式表示联合概率。
3.7 条件随机场(CRF)
条件随机场(Conditional Random Field,CRF):
给定MRF中的每个随机变量下面还有观测值,则给定观测条件下MRF的分布:
其中,x为观测集合。
- tany 2017年10月7日于杭州
人工智能从入门到专家教程资料:https://item.taobao.com/item.htm?spm=a1z38n.10677092.0.0.38270209gU11fS&id=562189023765