keras之父《python深度学习》笔记 第五章
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
深度学习用于计算机视觉
- 前言
- 一、卷积神经网络介绍
-
- 1.卷积神经网络简介
- 2.卷积网络特点
- 3.卷积网络中一些重要操作
- 4.池化层
- 二、在一个小数据集上从头训练一个卷积神经网络
-
- 1.深度学习处理小数据问题
- 2.获取数据
- 3.构建网络
- 4.数据预处理
- 5.进行数据增强
- 三、使用预训练模型
-
- 1.特征提取
- 2.模型微调
- 总结
前言
原书是分为上下两部分,上部理论更多,下部更偏实战,这是下部的第一章,深度学习用于计算机视觉
提示:以下是本篇文章正文内容,下面案例可供参考
一、卷积神经网络介绍
卷积神经网络,也叫convnet,几乎所有的计算机视觉神经网络都用到了卷积神经网络。
1.卷积神经网络简介
首先跟大家展示一个简单的神经网络,就是我们之前看到的MNIST数字分类。这个任务之前我们使用全连接层进行训练的,本例中我们采用简单的卷积神经网络再做一次。
from keras import layers
from keras import models
model = models.Sequential()
model.add(layers.Conv2D(32, (3, 3), activation='relu', input_shape=(28, 28, 1)))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(64, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(64, (3, 3), activation='relu'))
卷积神经网络接收形状为(image_height,image_width,image_channels)的输入张量。本例中处理的是(28,28,1)的输入张量,这就是MNIST的数据格式。
keras中可以很方便的看到神经网络的架构。
>>> model.summary()
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
conv2d_1 (Conv2D) (None, 26, 26, 32) 320
_________________________________________________________________
max_pooling2d_1 (MaxPooling2D) (None, 13, 13, 32) 0
_________________________________________________________________
conv2d_2 (Conv2D) (None, 11, 11, 64) 18496
_________________________________________________________________
max_pooling2d_2 (MaxPooling2D) (None, 5, 5, 64) 0
_________________________________________________________________
conv2d_3 (Conv2D) (None, 3, 3, 64) 36928
=================================================================
Total params: 55,744
Trainable params: 55,744
Non-trainable params: 0
可以看到,每个Conv2D 层和MaxPooling2D 层的输出都是一个形状为(height, width,channels) 的3D 张量。宽度和高度两个维度的尺寸通常会随着网络加深而变小。通道数量由传入Conv2D 层的第一个参数所控制(32 或64)。
下一步是将最后的输出张量[大小为(3, 3, 64)]输入到一个密集连接分类器网络中,即Dense 层的堆叠,你已经很熟悉了。这些分类器可以处理1D 向量,而当前的输出是3D 张量。首先,我们需要将3D 输出展平为1D,然后在上面添加几个Dense 层。
model.add(layers.Flatten())
model.add(layers.Dense(64, activation='relu'))
model.add(layers.Dense(10, activation='softmax'))
在添加分类层之后,再来看一下网络架构
>>> model.summary()
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
conv2d_1 (Conv2D) (None, 26, 26, 32) 320
_________________________________________________________________
max_pooling2d_1 (MaxPooling2D) (None, 13, 13, 32) 0
_________________________________________________________________
conv2d_2 (Conv2D) (None, 11, 11, 64) 18496
_________________________________________________________________
max_pooling2d_2 (MaxPooling2D) (None, 5, 5, 64) 0
_________________________________________________________________
conv2d_3 (Conv2D) (None, 3, 3, 64) 36928
________________________________________________________________
flatten_1 (Flatten) (None, 576) 0
_________________________________________________________________
dense_1 (Dense) (None, 64) 36928
_________________________________________________________________
dense_2 (Dense) (None, 10) 650
=================================================================
Total params: 93,322
Trainable params: 93,322
Non-trainable params: 0
如你所见,在进入两个Dense 层之前,形状(3, 3, 64) 的输出被展平为形状(576,) 的向量。
接下来是train模型的过程。
from keras.datasets import mnist
from keras.utils import to_categorical
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
train_images = train_images.reshape((60000, 28, 28, 1))
train_images = train_images.astype('float32') / 255
test_images = test_images.reshape((10000, 28, 28, 1))
test_images = test_images.astype('float32') / 255
train_labels = to_categorical(train_labels)
test_labels = to_categorical(test_labels)
model.compile(optimizer='rmsprop',
loss='categorical_crossentropy',
metrics=['accuracy'])
model.fit(train_images, train_labels, epochs=5, batch_size=64)
train完之后评估一下结果
>>> test_loss, test_acc = model.evaluate(test_images, test_labels)
>>> test_acc
0.99080000000000001
相比于全连接层97.8%左右的测试精度,卷积网络的精度更高(随着精度变高提升的困难其实是越来越大的,所以这个提升可以说是很大的提升了)。下面我们就了解一下卷及网路的作用。
2.卷积网络特点
密集连接层和卷积层的根本区别在于,Dense 层从输入特征空间中学到的是全局模式(比如对于MNIST 数字,全局模式就是涉及所有像素的模式),而卷积层学到的是局部模式,对于图像来说,学到的就是在输入图像的二维小窗口中发现的模式。在上面的例子中,这些窗口的大小都是3×3。
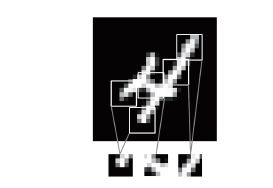
卷积网络局部学习模式的特征有几个有趣的性质:
1.卷积神经网络学到的模式具有平移不变性(translation invariant)。卷积神经网络在图像右下角学到某个模式之后,它可以在任何地方识别这个模式,比如左上角。对于密集连接网络来说,如果模式出现在新的位置,它只能重新学习这个模式。这使得卷积神经网络在处理图像时可以高效利用数据(因为视觉世界从根本上具有平移不变性),它只需要更少的训练样本就可以学到具有泛化能力的数据表示。
2.卷积神经网络可以学到模式的空间层次结构(spatial hierarchies of patterns)第一个卷积层将学习较小的局部模式(比如边缘),第二个卷积层将学习由第一层特征组成的更大的模式,以此类推。这使得卷积神经网络可以有效地学习越来越复杂、越来越抽象的视觉概念(因为视觉世界从根本上具有空间层次结构)。
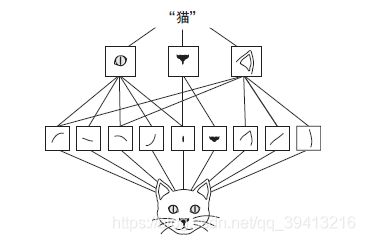
在MNIST 示例中,第一个卷积层接收一个大小为(28, 28, 1) 的特征图,并输出一个大小为(26, 26, 32) 的特征图,即它在输入上计算32 个过滤器。对于这32 个输出通道,每个通道都包含一个26×26 的数值网格,它是过滤器对输入的响应图(response map),表示这个过滤器模式在输入中不同位置的响应)。这也是特征图这一术语的含义:深度轴的每个
维度都是一个特征(或过滤器),而2D 张量output[:, :, n] 是这个过滤器在输入上的响应的二维空间图(map)。
卷积由以下两个关键参数所定义。
从输入中提取的图块尺寸:这些图块的大小通常是 3×3 或 5×5。本例中为 3×3,这是
很常见的选择。
输出特征图的深度:卷积所计算的过滤器的数量。本例第一层的深度为32,最后一层的深度是64。
对于Keras 的Conv2D 层,这些参数都是向层传入的前几个参数:Conv2D(output_depth,(window_height, window_width))。
卷积的工作原理:在3D 输入特征图上滑动(slide)这些3×3 或5×5 的窗口,在每个可能的位置停止并提取周围特征的3D 图块[形状为(window_height, window_width, input_depth)]。然后每个3D 图块与学到的同一个权重矩阵[叫作卷积核(convolution kernel)]做张量积,转换成形状为(output_depth,) 的1D 向量。然后对所有这些向量进行空间重组,使其转换为形状为(height, width, output_depth) 的3D 输出特征图。输出特征图中的每个空间位置都对应于输入特征图中的相同位置(比如输出的右下角包含输入右下角的信息)。举个例子,利用3×3 的窗口,向量output[i, j, :] 来自3D 图块input[i-1:i+1,j-1:j+1, :]。整个过程详见下图
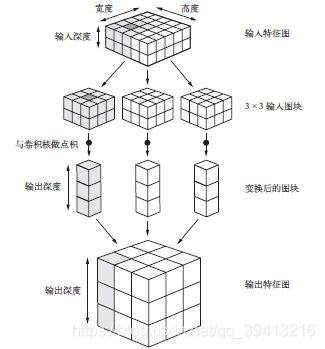
注意,输出的宽度和高度可能与输入的宽度和高度不同。不同的原因可能有两点。
边界效应,可以通过对输入特征图进行填充来抵消。
使用了步幅(stride),稍后会给出其定义。
3.卷积网络中一些重要操作
理解边界效应与填充
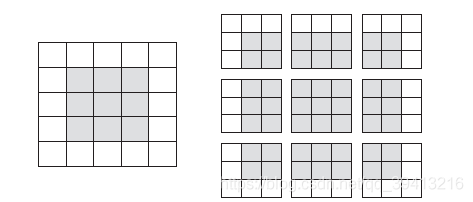
假设有一个5×5 的特征图(共25 个方块)。其中只有9 个方块可以作为中心放入一个3×3 的窗口,这9 个方块形成一个3×3 的网格(见图5-5)。因此,输出特征图的尺寸是3×3。它比输入尺寸小了一点,在本例中沿着每个维度都正好缩小了2 个方块。在前一个例子中你也可以看到这种边界效应的作用:开始的输入尺寸为28×28,经过第一个卷积层之后尺寸变为
26×26。
如果你希望输出特征图的空间维度与输入相同,那么可以使用填充(padding)。填充是在输入特征图的每一边添加适当数目的行和列,使得每个输入方块都能作为卷积窗口的中心。对于3×3 的窗口,在左右各添加一列,在上下各添加一行。对于5×5 的窗口,各添加两行和两列。
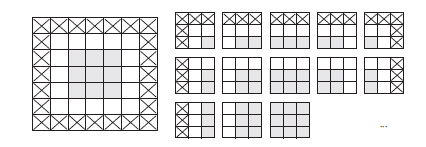
对于Conv2D 层,可以通过padding 参数来设置填充,这个参数有两个取值:“valid” 表示不使用填充(只使用有效的窗口位置);“same” 表示“填充后输出的宽度和高度与输入相同”。padding 参数的默认值为"valid"。
理解卷积步幅
影响输出尺寸的另一个因素是步幅的概念。目前为止,对卷积的描述都假设卷积窗口的中
心方块都是相邻的。但两个连续窗口的距离是卷积的一个参数,叫作步幅,默认值为1。也可以使用步进卷积(strided convolution),即步幅大于1 的卷积。也有用步幅为2 的3×3 卷积从5×5 输入中提取的图块(无填充)。
步幅为2 意味着特征图的宽度和高度都被做了2 倍下采样(除了边界效应引起的变化)。虽然步进卷积对某些类型的模型可能有用,但在实践中很少使用。熟悉这个概念是有好处的。为了对特征图进行下采样,我们不用步幅,而是通常使用最大池化(max-pooling)运算,你在第一个卷积神经网络示例中见过此运算。下面我们来深入研究这种运算。
4.池化层
在卷积神经网络示例中,你可能注意到,在每个MaxPooling2D 层之后,特征图的尺寸都会减半。例如,在第一个MaxPooling2D 层之前,特征图的尺寸是26×26,但最大池化运算将其减半为13×13。这就是最大池化的作用:对特征图进行下采样,与步进卷积类似。
最大池化是从输入特征图中提取窗口,并输出每个通道的最大值。它的概念与卷积类似,但是最大池化使用硬编码的max 张量运算对局部图块进行变换,而不是使用学到的线性变换(卷
积核)。最大池化与卷积的最大不同之处在于,最大池化通常使用2×2 的窗口和步幅2,其目的是将特征图下采样2 倍。与此相对的是,卷积通常使用3×3 窗口和步幅1。
为什么要用这种方式对特征图下采样?为什么不删除最大池化层,一直保留较大的特征图?
我们来这么做试一下。这时模型的卷积基(convolutional base)如下所示。
model_no_max_pool = models.Sequential()
model_no_max_pool.add(layers.Conv2D(32, (3, 3), activation='relu',
input_shape=(28, 28, 1)))
model_no_max_pool.add(layers.Conv2D(64, (3, 3), activation='relu'))
model_no_max_pool.add(layers.Conv2D(64, (3, 3), activation='relu'))
模型结构如下
>>> model_no_max_pool.summary()
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
conv2d_4 (Conv2D) (None, 26, 26, 32) 320
_________________________________________________________________
conv2d_5 (Conv2D) (None, 24, 24, 64) 18496
_________________________________________________________________
conv2d_6 (Conv2D) (None, 22, 22, 64) 36928
=================================================================
Total params: 55,744
Trainable params: 55,744
这种架构有什么问题?有如下两点问题。
‰ 这种架构不利于学习特征的空间层级结构。第三层的 3×3 窗口中只包含初始输入的7×7 窗口中所包含的信息。卷积神经网络学到的高级模式相对于初始输入来说仍然很小,
这可能不足以学会对数字进行分类(你可以试试仅通过7 像素×7 像素的窗口观察图像来识别其中的数字)。我们需要让最后一个卷积层的特征包含输入的整体信息。
‰ 最后一层的特征图对每个样本共有 22×22×64=30 976 个元素。这太多了。如果你将其展平并在上面添加一个大小为512 的Dense 层,那一层将会有1580 万个参数。这对于这样一个小模型来说太多了,会导致严重的过拟合。
简而言之,使用下采样的原因,一是减少需要处理的特征图的元素个数,二是通过让连续卷积层的观察窗口越来越大(即窗口覆盖原始输入的比例越来越大),从而引入空间过滤器的层级结构。
注意,最大池化不是实现这种下采样的唯一方法。你已经知道,还可以在前一个卷积层中使用步幅来实现。此外,你还可以使用平均池化来代替最大池化,其方法是将每个局部输入图块变换为取该图块各通道的平均值,而不是最大值。但最大池化的效果往往比这些替代方法更好。
简而言之,原因在于特征中往往编码了某种模式或概念在特征图的不同位置是否存在(因此得名特征图),而观察不同特征的最大值而不是平均值能够给出更多的信息。因此,最合理的子采样策略是首先生成密集的特征图(通过无步进的卷积),然后观察特征每个小图块上的最大激活,而不是查看输入的稀疏窗口(通过步进卷积)或对输入图块取平均,因为后两种方法可能导致错过或淡化特征是否存在的信息。
现在你应该已经理解了卷积神经网络的基本概念,即特征图、卷积和最大池化,并且也知道如何构建一个小型卷积神经网络来解决简单问题,比如MNIST 数字分类。下面我们将介绍更加实用的应用。
二、在一个小数据集上从头训练一个卷积神经网络
1.深度学习处理小数据问题
在正常情况下,深度学习是需要大量数据来训练模型的。但是对于初学者来说,获取大量数据是比较难的。其实在简单的任务中,把模型尽量做小,然后尽量做好正则化,也是可以活着很好的效果的。因为卷积网络学习到的都是局部的,平移不动的特征,它对于感知问题可以高效的利用数据。
我们打算在一个4000张的猫狗图像集上来做训练一个卷积神经网络。
2.获取数据
这个数据集不在keras当中,我们需要去kaggle当中下载原始数据集,地址为:https://www.kaggle.com/c/dogs-vs-cats/data
kaggle是一个深度学习竞赛网站,里面有很多的机器学习的比赛,也提供了很多比赛用的数据集。
我满来看几张图片感受一个这个数据集的内容:

不出所料,2013 年的猫狗分类Kaggle 竞赛的优胜者使用的是卷积神经网络。最佳结果达到了95% 的精度。本例中,虽然你只在不到参赛选手所用的10% 的数据上训练模型,但结果也和这个精度相当接近(见下一节)。
这个数据集包含25 000 张猫狗图像(每个类别都有12 500 张),大小为543MB(压缩后)。下载数据并解压之后,你需要创建一个新数据集,其中包含三个子集:每个类别各1000 个样本
的训练集、每个类别各500 个样本的验证集和每个类别各500 个样本的测试集。
import os, shutil
original_dataset_dir = '/Users/fchollet/Downloads/kaggle_original_data'
base_dir = '/Users/fchollet/Downloads/cats_and_dogs_small'
os.mkdir(base_dir)
train_dir = os.path.join(base_dir, 'train')
os.mkdir(train_dir)
validation_dir = os.path.join(base_dir, 'validation')
os.mkdir(validation_dir)
test_dir = os.path.join(base_dir, 'test')
os.mkdir(test_dir)
train_cats_dir = os.path.join(train_dir, 'cats')
os.mkdir(train_cats_dir)
train_dogs_dir = os.path.join(train_dir, 'dogs')
os.mkdir(train_dogs_dir)
validation_cats_dir = os.path.join(validation_dir, 'cats')
os.mkdir(validation_cats_dir)
validation_dogs_dir = os.path.join(validation_dir, 'dogs')
os.mkdir(validation_dogs_dir)
test_cats_dir = os.path.join(test_dir, 'cats')
os.mkdir(test_cats_dir)
test_dogs_dir = os.path.join(test_dir, 'dogs')
os.mkdir(test_dogs_dir)
fnames = ['cat.{}.jpg'.format(i) for i in range(1000)]
for fname in fnames:
src = os.path.join(original_dataset_dir, fname)
dst = os.path.join(train_cats_dir, fname)
shutil.copyfile(src, dst)
fnames = ['cat.{}.jpg'.format(i) for i in range(1000, 1500)]
for fname in fnames:
src = os.path.join(original_dataset_dir, fname)
dst = os.path.join(validation_cats_dir, fname)
shutil.copyfile(src, dst)
fnames = ['cat.{}.jpg'.format(i) for i in range(1500, 2000)]
for fname in fnames:
src = os.path.join(original_dataset_dir, fname)
dst = os.path.join(test_cats_dir, fname)
shutil.copyfile(src, dst)
fnames = ['dog.{}.jpg'.format(i) for i in range(1000)]
for fname in fnames:
src = os.path.join(original_dataset_dir, fname)
dst = os.path.join(train_dogs_dir, fname)
shutil.copyfile(src, dst)
fnames = ['dog.{}.jpg'.format(i) for i in range(1000, 1500)]
for fname in fnames:
src = os.path.join(original_dataset_dir, fname)
dst = os.path.join(validation_dogs_dir, fname)
shutil.copyfile(src, dst)
fnames = ['dog.{}.jpg'.format(i) for i in range(1500, 2000)]
for fname in fnames:
src = os.path.join(original_dataset_dir, fname)
dst = os.path.join(test_dogs_dir, fname)
shutil.copyfile(src, dst)
我们来检查一下,看看每个分组(训练/ 验证/ 测试)中分别包含多少张图像。
>>> print('total training cat images:', len(os.listdir(train_cats_dir)))
total training cat images: 1000
>>> print('total training dog images:', len(os.listdir(train_dogs_dir)))
total training dog images: 1000
>>> print('total validation cat images:', len(os.listdir(validation_cats_dir)))
total validation cat images: 500
>>> print('total validation dog images:', len(os.listdir(validation_dogs_dir)))
total validation dog images: 500
>>> print('total test cat images:', len(os.listdir(test_cats_dir)))
total test cat images: 500
>>> print('total test dog images:', len(os.listdir(test_dogs_dir)))
total test dog images: 500
所以我们的确有2000 张训练图像、1000 张验证图像和1000 张测试图像。每个分组中两个类别的样本数相同,这是一个平衡的二分类问题,分类精度可作为衡量成功的指标。
3.构建网络
在前一个MNIST 示例中,我们构建了一个小型卷积神经网络,所以你应该已经熟悉这
种网络。我们将复用相同的总体结构,即卷积神经网络由Conv2D 层(使用relu 激活)和MaxPooling2D 层交替堆叠构成。
但由于这里要处理的是更大的图像和更复杂的问题,你需要相应地增大网络,即再增加一个Conv2D+MaxPooling2D 的组合。这既可以增大网络容量,也可以进一步减小特征图的尺寸,使其在连接Flatten 层时尺寸不会太大。本例中初始输入的尺寸为150×150(有些随意的选择),所以最后在Flatten 层之前的特征图大小为7×7。
你面对的是一个二分类问题,所以网络最后一层是使用sigmoid 激活的单一单元(大小为1 的Dense 层)。这个单元将对某个类别的概率进行编码。
from keras import layers
from keras import models
model = models.Sequential()
model.add(layers.Conv2D(32, (3, 3), activation='relu',
input_shape=(150, 150, 3)))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(64, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(128, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(128, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Flatten())
model.add(layers.Dense(512, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))
我们来看一下特征图的维度如何随着每层变化。
>>> model.summary()
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
conv2d_1 (Conv2D) (None, 148, 148, 32) 896
_________________________________________________________________
max_pooling2d_1 (MaxPooling2D) (None, 74, 74, 32) 0
_________________________________________________________________
conv2d_2 (Conv2D) (None, 72, 72, 64) 18496
_________________________________________________________________
max_pooling2d_2 (MaxPooling2D) (None, 36, 36, 64) 0
_________________________________________________________________
conv2d_3 (Conv2D) (None, 34, 34, 128) 73856
_________________________________________________________________
max_pooling2d_3 (MaxPooling2D) (None, 17, 17, 128) 0
_________________________________________________________________
conv2d_4 (Conv2D) (None, 15, 15, 128) 147584
_________________________________________________________________
max_pooling2d_4 (MaxPooling2D) (None, 7, 7, 128) 0
_________________________________________________________________
flatten_1 (Flatten) (None, 6272) 0
_________________________________________________________________
dense_1 (Dense) (None, 512) 3211776
_________________________________________________________________
dense_2 (Dense) (None, 1) 513
=================================================================
Total params: 3,453,121
Trainable params: 3,453,1
在编译这一步,和前面一样,我们将使用RMSprop 优化器。因为网络最后一层是单一sigmoid单元,所以我们将使用二元交叉熵作为损失函数(提醒一下,表4-1 列出了各种情况下应该使用的损失函数)。
from keras import optimizers
model.compile(loss='binary_crossentropy',
optimizer=optimizers.RMSprop(lr=1e-4),
metrics=['acc'])
4.数据预处理
你现在已经知道,将数据输入神经网络之前,应该将数据格式化为经过预处理的浮点数张量。
现在,数据以JPEG 文件的形式保存在硬盘中,所以数据预处理步骤大致如下。
(1) 读取图像文件。
(2) 将JPEG 文件解码为RGB 像素网格。
(3) 将这些像素网格转换为浮点数张量。
(4) 将像素值(0~255 范围内)缩放到[0, 1] 区间(正如你所知,神经网络喜欢处理较小的输
入值)。
这些步骤可能看起来有点吓人,但幸运的是,Keras 拥有自动完成这些步骤的工具。Keras有一个图像处理辅助工具的模块,位于keras.preprocessing.image。特别地,它包含
ImageDataGenerator 类,可以快速创建Python 生成器,能够将硬盘上的图像文件自动转换为预处理好的张量批量。下面我们将用到这个类。
from keras.preprocessing.image import ImageDataGenerator
train_datagen = ImageDataGenerator(rescale=1./255)
test_datagen = ImageDataGenerator(rescale=1./255)
train_generator = train_datagen.flow_from_directory(
train_dir,
target_size=(150, 150),
batch_size=20,
class_mode='binary')
validation_generator = test_datagen.flow_from_directory(
validation_dir,
target_size=(150, 150),
batch_size=20,
class_mode='binary')
我们来看一下其中一个生成器的输出:它生成了150×150 的RGB 图像[形状为(20,
150, 150, 3)]与二进制标签[形状为(20,)]组成的批量。每个批量中包含20 个样本(批量大小)。注意,生成器会不停地生成这些批量,它会不断循环目标文件夹中的图像。因此,你需要在某个时刻终止(break)迭代循环。
需要在某个时刻终止(break)迭代循环。
>>> for data_batch, labels_batch in train_generator:
>>> print('data batch shape:', data_batch.shape)
>>> print('labels batch shape:', labels_batch.shape)
>>> break
data batch shape: (20, 150, 150, 3)
labels batch shape: (20,)
利用生成器,我们让模型对数据进行拟合。我们将使用fit_generator 方法来拟合,它在数据生成器上的效果和fit 相同。它的第一个参数应该是一个Python 生成器,可以不停地生成输入和目标组成的批量,比如train_generator。因为数据是不断生成的,所以Keras 模型要知道每一轮需要从生成器中抽取多少个样本。这是steps_per_epoch 参数的作用:从生成器中抽取steps_per_epoch 个批量后(即运行了steps_per_epoch 次梯度下降),拟合过程将进入下一个轮次。本例中,每个批量包含20 个样本,所以读取完所有2000 个样本需要100个批量。
使用fit_generator 时,你可以传入一个validation_data 参数,其作用和在fit 方法中类似。值得注意的是,这个参数可以是一个数据生成器,但也可以是Numpy 数组组成的元组。如果向validation_data 传入一个生成器,那么这个生成器应该能够不停地生成验证数据批量,因此你还需要指validation_steps 参数,说明需要从验证生成器中抽取多少个批次用于评估。
history = model.fit_generator(
train_generator,
steps_per_epoch=100,
epochs=30,
validation_data=validation_generator,
validation_steps=50)
model.save('cats_and_dogs_small_1.h5')
最后一行代码可以把训练的模型保存,以后可以直接加载保存的模型来预测。
import matplotlib.pyplot as plt
acc = history.history['acc']
val_acc = history.history['val_acc']
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(1, len(acc) + 1)
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.legend()
plt.figure()
plt.plot(epochs, loss, 'bo', label='Training loss')
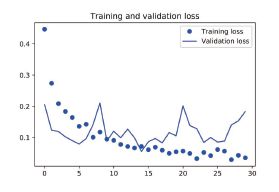
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.legend()
plt.show()
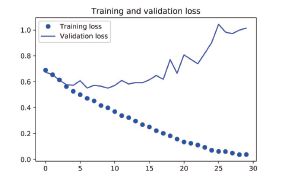
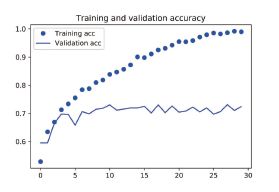
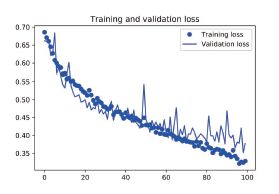
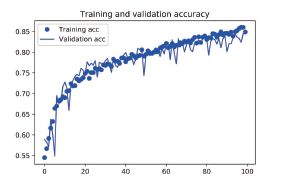
从这些图像中都能看出过拟合的特征。训练精度随着时间线性增加,直到接近100%,而验证精度则停留在70%~72%。验证损失仅在5 轮后就达到最小值,然后保持不变,而训练损失则
一直线性下降,直到接近于0。
因为训练样本相对较少(2000 个),所以过拟合是你最关心的问题。前面已经介绍过几种降低过拟合的技巧,比如dropout 和权重衰减(L2 正则化)。现在我们将使用一种针对于计算机视觉领域的新方法,在用深度学习模型处理图像时几乎都会用到这种方法,它就是数据增强(data augmentation)。
5.进行数据增强
过拟合的原因是学习样本太少,导致无法训练出能够泛化到新数据的模型。如果拥有无限的数据,那么模型能够观察到数据分布的所有内容,这样就永远不会过拟合。数据增强是从现有的训练样本中生成更多的训练数据,其方法是利用多种能够生成可信图像的随机变换来增加(augment)样本。其目标是,模型在训练时不会两次查看完全相同的图像。这让模型能够观察到数据的更多内容,从而具有更好的泛化能力。
datagen = ImageDataGenerator(
rotation_range=40,
width_shift_range=0.2,
height_shift_range=0.2,
shear_range=0.2,
zoom_range=0.2,
horizontal_flip=True,
fill_mode='nearest')
这里只选择了几个参数(想了解更多参数,请查阅Keras 文档)。我们来快速介绍一下这些
参数的含义。
‰ rotation_range是角度值(在 0~180 范围内),表示图像随机旋转的角度范围。
‰ width_shift 和 height_shift 是图像在水平或垂直方向上平移的范围(相对于总宽
度或总高度的比例)。
‰ shear_range是随机错切变换的角度。
‰ zoom_range是图像随机缩放的范围。
‰ horizontal_flip 是随机将一半图像水平翻转。如果没有水平不对称的假设(比如真
实世界的图像),这种做法是有意义的。
‰ fill_mode是用于填充新创建像素的方法,这些新像素可能来自于旋转或宽度/高度平移。
我们来看一下增强后的图像
from keras.preprocessing import image
fnames = [os.path.join(train_cats_dir, fname) for
fname in os.listdir(train_cats_dir)]
img_path = fnames[3]
img = image.load_img(img_path, target_size=(150, 150))
x = image.img_to_array(img)
x = x.reshape((1,) + x.shape)
i = 0
for batch in datagen.flow(x, batch_size=1):
plt.figure(i)
imgplot = plt.imshow(image.array_to_img(batch[0]))
i += 1
if i % 4 == 0:
break
plt.show()
通过这段代码可以看到数据增强之后的图片。遗憾的是数据增强在其他问题上不那么好用,只有在图片处理上特别好用,不然的话困扰深度学习的数据过少问题就可以解决了,
model = models.Sequential()
model.add(layers.Conv2D(32, (3, 3), activation='relu',
input_shape=(150, 150, 3)))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(64, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(128, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(128, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Flatten())
model.add(layers.Dropout(0.5))
model.add(layers.Dense(512, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))
model.compile(loss='binary_crossentropy',
optimizer=optimizers.RMSprop(lr=1e-4),
metrics=['acc'])
train_datagen = ImageDataGenerator(
rescale=1./255,
rotation_range=40,
width_shift_range=0.2,
height_shift_range=0.2,
zoom_range=0.2,
horizontal_flip=True,)
test_datagen = ImageDataGenerator(rescale=1./255)
train_generator = train_datagen.flow_from_directory(
train_dir,
target_size=(150, 150),
batch_size=32,
class_mode='binary')
validation_generator = test_datagen.flow_from_directory(
validation_dir,
target_size=(150, 150),
batch_size=32,
class_mode='binary')
history = model.fit_generator(
train_generator,
steps_per_epoch=100,
epochs=100,
validation_data=validation_generator,
validation_steps=50)
增强后的数据其实很多都是相似数据,为了防止过拟合我们在神经网络中加入了dropout来减少过拟合现象。
三、使用预训练模型
想要将深度学习应用于小型图像数据集,一种常用且非常高效的方法是使用预训练网络。预训练网络(pretrained network)是一个保存好的网络,之前已在大型数据集(通常是大规模图像分类任务)上训练好。如果这个原始数据集足够大且足够通用,那么预训练网络学到的特征的空间层次结构可以有效地作为视觉世界的通用模型,因此这些特征可用于各种不同的计算机视觉问题,即使这些新问题涉及的类别和原始任务完全不同。举个例子,在ImageNet 上训练了一个网络(其类别主要是动物和日常用品),然后将这个训练好的网络用于某个不相干的任务,比如在图像中识别家具。这种学到的特征在不同问题之间的可移植性,是深度学习与许多早期浅层学习方法相比的重要优势,它使得深度学习对小数据问题非常有效。本例中,假设有一个在ImageNet 数据集(140 万张标记图像,1000 个不同的类别)上训练好的大型卷积神经网络。ImageNet 中包含许多动物类别,其中包括不同种类的猫和狗,因此可以认为它在猫狗分类问题上也能有良好的表现。
我们将使用VGG16 架构,它由Karen Simonyan 和Andrew Zisserman 在2014 年开发。对于ImageNet,它是一种简单而又广泛使用的卷积神经网络架构。虽然VGG16 是一个比较旧的模型,性能远比不了当前最先进的模型,而且还比许多新模型更为复杂,但我之所以选择它,是因为它的架构与你已经熟悉的架构很相似,因此无须引入新概念就可以很好地理解。这可能是你第一次遇到这种奇怪的模型名称——VGG、ResNet、Inception、Inception-ResNet、Xception 等。
你会习惯这些名称的,因为如果你一直用深度学习做计算机视觉的话,它们会频繁出现。
使用预训练网络有两种方法:特征提取(feature extraction)和微调模型(fine-tuning)。两种方法我们都会介绍。首先来看特征提取。
1.特征提取
特征提取是使用之前网络学到的表示来从新样本中提取出有趣的特征。然后将这些特征输入一个新的分类器,从头开始训练。
如前所述,用于图像分类的卷积神经网络包含两部分:首先是一系列池化层和卷积层,最后是一个密集连接分类器。第一部分叫作模型的卷积基(convolutional base)。对于卷积神经网络而言,特征提取就是取出之前训练好的网络的卷积基,在上面运行新数据,然后在输出上面训练一个新的分类器。
为什么仅重复使用卷积基?我们能否也重复使用密集连接分类器?一般来说,应该避免这么做。原因在于卷积基学到的表示可能更加通用,因此更适合重复使用。卷积神经网络的特征图表示通用概念在图像中是否存在,无论面对什么样的计算机视觉问题,这种特征图都可能很有用。但是,分类器学到的表示必然是针对于模型训练的类别,其中仅包含某个类别出现在整张图像中的概率信息。此外,密集连接层的表示不再包含物体在输入图像中的位置信息。密集连接层舍弃了空间的概念,而物体位置信息仍然由卷积特征图所描述。如果物体位置对于问题很重要,那么密集连接层的特征在很大程度上是无用的。
注意,某个卷积层提取的表示的通用性(以及可复用性)取决于该层在模型中的深度。模型中更靠近底部的层提取的是局部的、高度通用的特征图(比如视觉边缘、颜色和纹理),而更靠近顶部的层提取的是更加抽象的概念(比如“猫耳朵”或“狗眼睛”)。a 因此,如果你的新数据集与原始模型训练的数据集有很大差异,那么最好只使用模型的前几层来做特征提取,而不是使用整个卷积基。
本例中,由于ImageNet 的类别中包含多种狗和猫的类别,所以重复使用原始模型密集连接层中所包含的信息可能很有用。但我们选择不这么做,以便涵盖新问题的类别与原始模型的类别不一致的更一般情况。我们来实践一下,使用在ImageNet 上训练的VGG16 网络的卷积基从猫狗图像中提取有趣的特征,然后在这些特征上训练一个猫狗分类器。
VGG16 等模型内置于Keras 中。你可以从keras.applications 模块中导入。下面是keras.applications 中的一部分图像分类模型(都是在ImageNet 数据集上预训练得到的):
‰ Xception
‰ Inception V3
‰ ResNet50
‰ VGG16
‰ VGG19
‰ MobileNet
我们将VGG16 模型实例化。
from keras.applications import VGG16
conv_base = VGG16(weights='imagenet',
include_top=False,
input_shape=(150, 150, 3))
这里向构造函数中传入了三个参数。
‰ weights指定模型初始化的权重检查点。
‰ include_top 指定模型最后是否包含密集连接分类器。默认情况下,这个密集连接分
类器对应于ImageNet 的1000 个类别。因为我们打算使用自己的密集连接分类器(只有
两个类别:cat 和dog),所以不需要包含它。
‰ input_shape 是输入到网络中的图像张量的形状。这个参数完全是可选的,如果不传
入这个参数,那么网络能够处理任意形状的输入。
VGG16 卷积基的详细架构如下所示。它和你已经熟悉的简单卷积神经网络很相似。
>>> conv_base.summary()
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_1 (InputLayer) (None, 150, 150, 3) 0
_________________________________________________________________
block1_conv1 (Conv2D) (None, 150, 150, 64) 1792
_________________________________________________________________
block1_conv2 (Conv2D) (None, 150, 150, 64) 36928
_________________________________________________________________
block1_pool (MaxPooling2D) (None, 75, 75, 64) 0
_________________________________________________________________
block2_conv1 (Conv2D) (None, 75, 75, 128) 73856
_________________________________________________________________
block2_conv2 (Conv2D) (None, 75, 75, 128) 147584
_________________________________________________________________
block2_pool (MaxPooling2D) (None, 37, 37, 128) 0
_________________________________________________________________
block3_conv1 (Conv2D) (None, 37, 37, 256) 295168
_________________________________________________________________
block3_conv2 (Conv2D) (None, 37, 37, 256) 590080
_________________________________________________________________
block3_conv3 (Conv2D) (None, 37, 37, 256) 590080
_________________________________________________________________
block3_pool (MaxPooling2D) (None, 18, 18, 256) 0
_________________________________________________________________
block4_conv1 (Conv2D) (None, 18, 18, 512) 1180160
_________________________________________________________________
block4_conv2 (Conv2D) (None, 18, 18, 512) 2359808
_________________________________________________________________
block4_conv3 (Conv2D) (None, 18, 18, 512) 2359808
_________________________________________________________________
block4_pool (MaxPooling2D) (None, 9, 9, 512) 0
_________________________________________________________________
block5_conv1 (Conv2D) (None, 9, 9, 512) 2359808
_________________________________________________________________
block5_conv2 (Conv2D) (None, 9, 9, 512) 2359808
_________________________________________________________________
block5_conv3 (Conv2D) (None, 9, 9, 512) 2359808
_________________________________________________________________
block5_pool (MaxPooling2D) (None, 4, 4, 512) 0
=================================================================
Total params: 14,714,688
Trainable params: 14,714,688
Non-trainable params: 0
最后的特征图形状为(4, 4, 512)。我们将在这个特征上添加一个密集连接分类器。
接下来,下一步有两种方法可供选择。
‰ 在你的数据集上运行卷积基,将输出保存成硬盘中的Numpy 数组,然后用这个数据作为输入,输入到独立的密集连接分类器中(与本书第一部分介绍的分类器类似)。这种方法速度快,计算代价低,因为对于每个输入图像只需运行一次卷积基,而卷积基是目前流程中计算代价最高的。但出于同样的原因,这种方法不允许你使用数据增强。
‰ 在顶部添加 Dense 层来扩展已有模型(即 conv_base),并在输入数据上端到端地运行
整个模型。这样你可以使用数据增强,因为每个输入图像进入模型时都会经过卷积基。
但出于同样的原因,这种方法的计算代价比第一种要高很多。
这两种方法我们都会介绍。首先来看第一种方法的代码:保存你的数据在conv_base 中的输出,然后将这些输出作为输入用于新模型。
- 不使用数据增强的快速特征提取
首先,运行ImageDataGenerator 实例,将图像及其标签提取为Numpy 数组。我们需要调用conv_base 模型的predict 方法来从这些图像中提取特征。
import numpy as np
from keras.preprocessing.image import ImageDataGenerator
base_dir = '/Users/fchollet/Downloads/cats_and_dogs_small'
train_dir = os.path.join(base_dir, 'train')
validation_dir = os.path.join(base_dir, 'validation')
test_dir = os.path.join(base_dir, 'test')
datagen = ImageDataGenerator(rescale=1./255)
batch_size = 20
def extract_features(directory, sample_count):
features = np.zeros(shape=(sample_count, 4, 4, 512))
labels = np.zeros(shape=(sample_count))
generator = datagen.flow_from_directory(
directory,
target_size=(150, 150),
batch_size=batch_size,
class_mode='binary')
i = 0
for inputs_batch, labels_batch in generator:
features_batch = conv_base.predict(inputs_batch)
features[i * batch_size : (i + 1) * batch_size] = features_batch
labels[i * batch_size : (i + 1) * batch_size] = labels_batch
i += 1
if i * batch_size >= sample_count:
break
return features, labels
train_features, train_labels = extract_features(train_dir, 2000)
validation_features, validation_labels = extract_features(validation_dir, 1000)
test_features, test_labels = extract_features(test_dir, 1000)
目前,提取的特征形状为(samples, 4, 4, 512)。我们要将其输入到密集连接分类器中,所以首先必须将其形状展平为(samples, 8192)。
train_features = np.reshape(train_features, (2000, 4 * 4 * 512))
validation_features = np.reshape(validation_features, (1000, 4 * 4 * 512))
test_features = np.reshape(test_features, (1000, 4 * 4 * 512))
现在你可以定义你的密集连接分类器(注意要使用dropout 正则化),并在刚刚保存的数据和标签上训练这个分类器。
from keras import models
from keras import layers
from keras import optimizers
model = models.Sequential()
model.add(layers.Dense(256, activation='relu', input_dim=4 * 4 * 512))
model.add(layers.Dropout(0.5))
model.add(layers.Dense(1, activation='sigmoid'))
model.compile(optimizer=optimizers.RMSprop(lr=2e-5),
loss='binary_crossentropy',
metrics=['acc'])
history = model.fit(train_features, train_labels,
epochs=30,
batch_size=20,
validation_data=(validation_features, validation_labels))
训练速度非常快,因为你只需处理两个Dense 层。即使在CPU 上运行,每轮的时间也不到一秒钟。
我们来看一下训练期间的损失曲线和精度曲线
import matplotlib.pyplot as plt
acc = history.history['acc']
val_acc = history.history['val_acc']
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(1, len(acc) + 1)
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.legend()
plt.figure()
plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.legend()
plt.show()
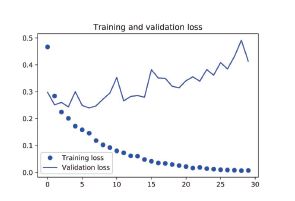
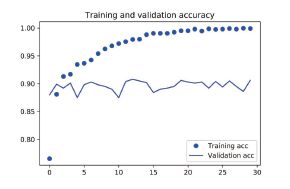
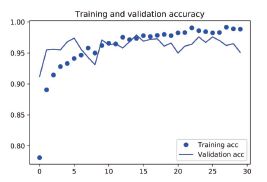
我们的验证精度达到了约90%,比上一节从头开始训练的小型模型效果要好得多。但从图
中也可以看出,虽然dropout 比率相当大,但模型几乎从一开始就过拟合。这是因为本方法没有
使用数据增强,而数据增强对防止小型图像数据集的过拟合非常重要。
2. 使用数据增强的特征提取
下面我们来看一下特征提取的第二种方法,它的速度更慢,计算代价更高,但在训练期间
可以使用数据增强。这种方法就是:扩展conv_base 模型,然后在输入数据上端到端地运行模型。
模型的行为和层类似,所以你可以向Sequential 模型中添加一个模型(比如conv_base),就像添加一个层一样。
from keras import models
from keras import layers
model = models.Sequential()
model.add(conv_base)
model.add(layers.Flatten())
model.add(layers.Dense(256, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))
>>> model.summary()
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
vgg16 (Model) (None, 4, 4, 512) 14714688
_________________________________________________________________
flatten_1 (Flatten) (None, 8192) 0
_________________________________________________________________
dense_1 (Dense) (None, 256) 2097408
_________________________________________________________________
dense_2 (Dense) (None, 1) 257
=================================================================
Total params: 16,812,353
Trainable params: 16,812,353
Non-trainable params: 0
如你所见,VGG16 的卷积基有14 714 688 个参数,非常多。在其上添加的分类器有200 万个参数。
在编译和训练模型之前,一定要“冻结”卷积基。冻结(freeze)一个或多个层是指在训练过程中保持其权重不变。如果不这么做,那么卷积基之前学到的表示将会在训练过程中被修改。
因为其上添加的Dense 层是随机初始化的,所以非常大的权重更新将会在网络中传播,对之前学到的表示造成很大破坏。
在Keras 中,冻结网络的方法是将其trainable 属性设为False。
>>> print('This is the number of trainable weights '
'before freezing the conv base:', len(model.trainable_weights))
This is the number of trainable weights before freezing the conv base: 30
>>> conv_base.trainable = False
>>> print('This is the number of trainable weights '
'after freezing the conv base:', len(model.trainable_weights))
This is the number of trainable weights after freezing the conv base: 4
如此设置之后,只有添加的两个Dense 层的权重才会被训练。总共有4 个权重张量,每层2 个(主权重矩阵和偏置向量)。注意,为了让这些修改生效,你必须先编译模型。如果在编译之后修改了权重的trainable 属性,那么应该重新编译模型,否则这些修改将被忽略。
现在你可以开始训练模型了,使用和前一个例子相同的数据增强设置。
from keras.preprocessing.image import ImageDataGenerator
from keras import optimizers
train_datagen = ImageDataGenerator(
rescale=1./255,
rotation_range=40,
width_shift_range=0.2,
height_shift_range=0.2,
shear_range=0.2,
zoom_range=0.2,
horizontal_flip=True,
fill_mode='nearest')
test_datagen = ImageDataGenerator(rescale=1./255)
train_generator = train_datagen.flow_from_directory(
train_dir,
target_size=(150, 150),
batch_size=20,
class_mode='binary')
validation_generator = test_datagen.flow_from_directory(
validation_dir,
target_size=(150, 150),
batch_size=20,
class_mode='binary')
model.compile(loss='binary_crossentropy',
optimizer=optimizers.RMSprop(lr=2e-5),
metrics=['acc'])
history = model.fit_generator(
train_generator,
steps_per_epoch=100,
epochs=30,
validation_data=validation_generator,
validation_steps=50)
2.模型微调
另一种广泛使用的模型复用方法是模型微调(fine-tuning),与特征提取互为补充。对于用
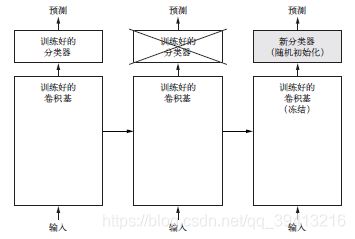
于特征提取的冻结的模型基,微调是指将其顶部的几层“解冻”,并将这解冻的几层和新增加的部分(本例中是全连接分类器)联合训练(见图5-19)。之所以叫作微调,是因为它只是略微调整了所复用模型中更加抽象的表示,以便让这些表示与手头的问题更加相关。
前面说过,冻结VGG16 的卷积基是为了能够在上面训练一个随机初始化的分类器。同理,
只有上面的分类器已经训练好了,才能微调卷积基的顶部几层。如果分类器没有训练好,那么训练期间通过网络传播的误差信号会特别大,微调的几层之前学到的表示都会被破坏。因此,微调网络的步骤如下。
(1) 在已经训练好的基网络(base network)上添加自定义网络。
(2) 冻结基网络。
(3) 训练所添加的部分。
(4) 解冻基网络的一些层。
(5) 联合训练解冻的这些层和添加的部分。
你在做特征提取时已经完成了前三个步骤。我们继续进行第四步:先解冻conv_base,然后冻结其中的部分层。提醒一下,卷积基的架构如下所示。
>>> conv_base.summary()
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_1 (InputLayer) (None, 150, 150, 3) 0
_________________________________________________________________
block1_conv1 (Conv2D) (None, 150, 150, 64) 1792
_________________________________________________________________
block1_conv2 (Conv2D) (None, 150, 150, 64) 36928
_________________________________________________________________
block1_pool (MaxPooling2D) (None, 75, 75, 64) 0
_________________________________________________________________
block2_conv1 (Conv2D) (None, 75, 75, 128) 73856
_________________________________________________________________
block2_conv2 (Conv2D) (None, 75, 75, 128) 147584
_________________________________________________________________
block2_pool (MaxPooling2D) (None, 37, 37, 128) 0
_________________________________________________________________
block3_conv1 (Conv2D) (None, 37, 37, 256) 295168
_________________________________________________________________
block3_conv2 (Conv2D) (None, 37, 37, 256) 590080
_________________________________________________________________
block3_conv3 (Conv2D) (None, 37, 37, 256) 590080
_________________________________________________________________
block3_pool (MaxPooling2D) (None, 18, 18, 256) 0
_________________________________________________________________
block4_conv1 (Conv2D) (None, 18, 18, 512) 1180160
_________________________________________________________________
block4_conv2 (Conv2D) (None, 18, 18, 512) 2359808
_________________________________________________________________
block4_conv3 (Conv2D) (None, 18, 18, 512) 2359808
_________________________________________________________________
block4_pool (MaxPooling2D) (None, 9, 9, 512) 0
_________________________________________________________________
block5_conv1 (Conv2D) (None, 9, 9, 512) 2359808
_________________________________________________________________
block5_conv2 (Conv2D) (None, 9, 9, 512) 2359808
_________________________________________________________________
block5_conv3 (Conv2D) (None, 9, 9, 512) 2359808
_________________________________________________________________
block5_pool (MaxPooling2D) (None, 4, 4, 512) 0
=================================================================
Total params: 14,714,688
Trainable params: 14,714,688
Non-trainable params: 0
我们将微调最后三个卷积层,也就是说,直到block4_pool 的所有层都应该被冻结,而block5_conv1、block5_conv2 和block5_conv3 三层应该是可训练的。
为什么不微调更多层?为什么不微调整个卷积基?你当然可以这么做,但需要考虑以下几点。
‰ 卷积基中更靠底部的层编码的是更加通用的可复用特征,而更靠顶部的层编码的是更专业化的特征。微调这些更专业化的特征更加有用,因为它们需要在你的新问题上改变用途。微调更靠底部的层,得到的回报会更少。
‰ 训练的参数越多,过拟合的风险越大。卷积基有 1500 万个参数,所以在你的小型数据集上训练这么多参数是有风险的。
因此,在这种情况下,一个好策略是仅微调卷积基最后的两三层。我们从上一个例子结束的地方开始,继续实现此方法。
conv_base.trainable = True
set_trainable = False
for layer in conv_base.layers:
if layer.name == 'block5_conv1':
set_trainable = True
if set_trainable:
layer.trainable = True
else:
layer.trainable = False
现在你可以开始微调网络。我们将使用学习率非常小的RMSProp 优化器来实现。之所以让
学习率很小,是因为对于微调的三层表示,我们希望其变化范围不要太大。太大的权重更新可能会破坏这些表示。
model.compile(loss='binary_crossentropy',
optimizer=optimizers.RMSprop(lr=1e-5),
metrics=['acc'])
history = model.fit_generator(
train_generator,
steps_per_epoch=100,
epochs=100,
validation_data=validation_generator,
validation_steps=50)
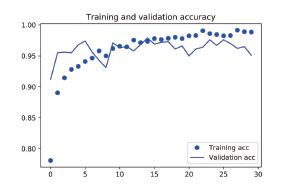
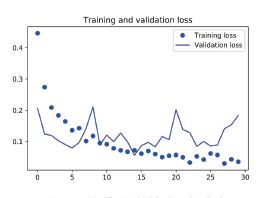
这些曲线看起来包含噪声。为了让图像更具可读性,你可以将每个损失和精度都替换为指数移动平均值,从而让曲线变得平滑。下面用一个简单的实用函数来实现
def smooth_curve(points, factor=0.8):
smoothed_points = []
for point in points:
if smoothed_points:
previous = smoothed_points[-1]
smoothed_points.append(previous * factor + point * (1 - factor))
else:
smoothed_points.append(point)
return smoothed_points
plt.plot(epochs,
smooth_curve(acc), 'bo', label='Smoothed training acc')
plt.plot(epochs,
smooth_curve(val_acc), 'b', label='Smoothed validation acc')
plt.title('Training and validation accuracy')
plt.legend()
plt.figure()
plt.plot(epochs,
smooth_curve(loss), 'bo', label='Smoothed training loss')
plt.plot(epochs,
smooth_curve(val_loss), 'b', label='Smoothed validation loss')
plt.title('Training and validation loss')
plt.legend()
plt.show()
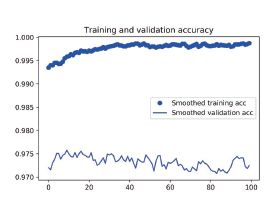
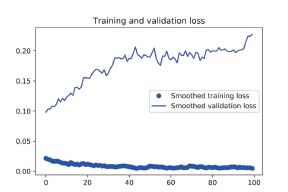
验证精度曲线变得更清楚。可以看到,精度值提高了1%,从约96% 提高到97% 以上。
注意,从损失曲线上看不出与之前相比有任何真正的提高(实际上还在变差)。你可能感到奇怪,如果损失没有降低,那么精度怎么能保持稳定或提高呢?答案很简单:图中展示的是逐
点(pointwise)损失值的平均值,但影响精度的是损失值的分布,而不是平均值,因为精度是模型预测的类别概率的二进制阈值。即使从平均损失中无法看出,但模型也仍然可能在改进。
现在,你可以在测试数据上最终评估这个模型。
test_generator = test_datagen.flow_from_directory(
test_dir,
target_size=(150, 150),
batch_size=20,
class_mode='binary')
test_loss, test_acc = model.evaluate_generator(test_generator, steps=50)
print('test acc:', test_acc)
我们得到了97% 的测试精度。在关于这个数据集的原始Kaggle 竞赛中,这个结果是最佳
结果之一。但利用现代深度学习技术,你只用一小部分训练数据(约10%)就得到了这个结果。
训练20 000 个样本与训练2000 个样本是有很大差别的!
总结
本文带大家实现了神经网络的两个途径,从头开始训练和采用预训练模型。学完之后可以用卷积网络来解决图像问题。由于imagenet的存在,世界上常用的简单的图像问题都可以通过预训练来解决掉,这对于缺少计算资源和数据的开发者来说是一个福音。