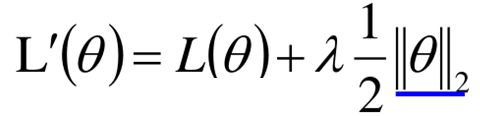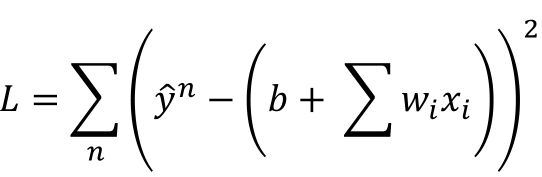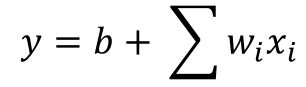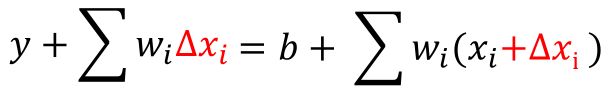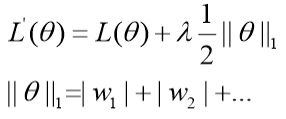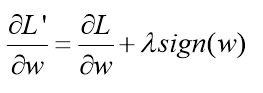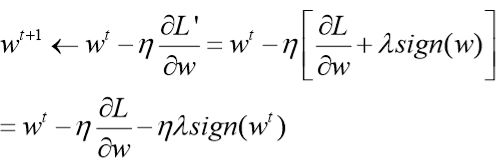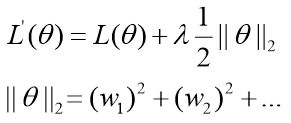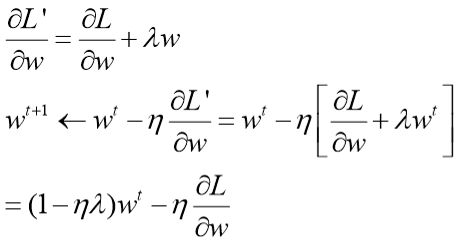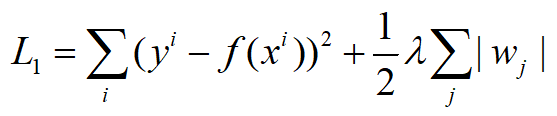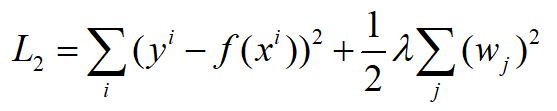本节主要是填前面的坑,前面要对正则化,以及多分类的问题进行一个单独总结,这里就通过搜集一些网上资料对这两块内容进行一个总结。
1.正则化
正则化是一种回归形式,为了防止模型的过拟合的方法,它将系数估计(coefficient estimate)朝零的方向进行约束、调整或缩小。
也就是说,正则化可以在学习过程中降低模型复杂度和不稳定程度,从而避免过拟合的危险。
正则化分为L1正则和L2正则,L1正则化和L2正则化都是在损失函数中加入惩罚项,以限制某些参数,L1正则又称Lasso回归,L2正则又称Ridge回归。如下式:
其中θ为参数:
||θ||为正则项,从上面的新的损失函数可以看出,在训练时不仅需要L(θ)最小,而且还要参数越小越好,这就相当于在学习时期望将一些不重要的特征权重减小。
那么为什么要使得权重越小越好呢,我们看下面的式子:
原始的损失函数为:
那么当Δx→0,原方程等价于:
当x很小的时候,w也要尽可能小,这不相当于在x之后再插入一个很微小的距离,插入一个点,使得y这条线更加的平滑吗。
那么L1和L2正则化是如何对训练产生影响呢?下面从数学公式的角度来说明:
当||θ||为L1正则时:
那么新的损失函数对参数的导致:
从上面的式子可以看出,前面两项跟原来的更新方式一样,而最后一项,当w>0时,会减去ηλ一项,而当w<0时,则会加上ηλ一项,说明更新时总是迫使参数朝着0的位置移动。
当||θ||是L2正则时:
那么新的损失函数对参数进行求导:
可以看出,参数的更新每次都要乘以1-ηλ, 那么第一项就会越来越小,逐渐趋于0,而后面那一项对于对损失有影响的项,值较大,整体就不会等于0,但对于损失没有影响的项,也是接近于0,整体接近于0(但极少等于0),因此,这个过程使得最终对于学习没有用的参数的权重进行了减弱。
根据上面对比L1和L2,虽然二者都是使参数朝着0的方向移动,但是对于L2来说,当参数数值比较大时,对参数的惩罚比较强,因为是-wηλ,
这样(L2正则)就会使得结果更加的smooth(平滑),因为通常来说光滑的曲线更能反映真实的情况,但当λ设置过大时,过于光滑,惩罚过大,则会导致欠拟合。
L1正则是一视同仁地移动ηλ个距离。
综上,L2使得所有的参数都会很接近于0,但不会真正到达0,而L1因为无视参数大小,移动距离都一样,因此参数之间会差距较大,有的达到0。这样对于损失贡献不大的特征的参数就会被置为0。
上面是从公式的角度解释L1好L2的工作原理以及为什么L1会产生稀疏解,而L2不会产生稀疏解的原因。
下面我们从几何和优化的角度来看看L1和L2的原理:
首先把L1正则和L2正则写成正常的公式,即:
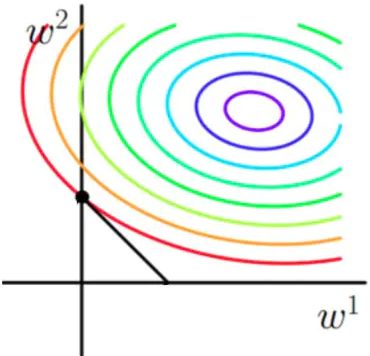
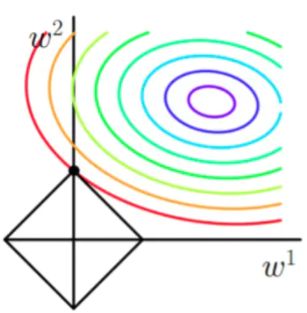
假设f(x)有两个参数w1和w2,那么原始的损失函数图像为:
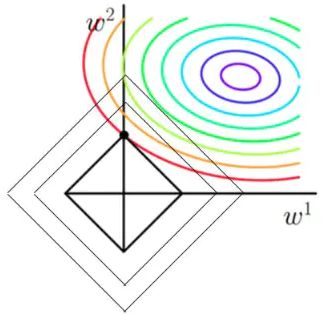
图中等高线代表了Loss的大小,对于L1,相当于在原损失函数中加入了后面|w|的限制,如若只有两个参数,那么后面那一项就是一个菱形,随着w的取值不同,菱形的大小也不同:
图中一方面要尽可能向着圆环的中心靠拢,另一方面又要使菱形最小,显然当菱形与等高线相切时是最小的,菱形与等高线的交点即为最优解,从图中可以看出,交点更靠近于远点,同时菱形也更容易相较于坐标轴上,从而使得某些维度的值为0;
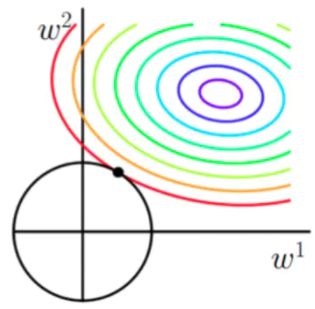
对于L2,后面一项为w12+w22,是一个圆形,如图所示:
对于圆形也是一样的道理,只不过在圆与等高线相交时,很难相较于坐标轴上,因此只会使得参数更加靠近原点,使得参数的平方和最小(最小圆)。
有关正则化的内容就说这么多,关键还是L1正则和L2正则的形式,以及L1能够产生稀疏解,L2会使得曲线更加的“光滑”,其实二者的本质都是降低模型的复杂程度以达到防止过拟合的。
2.多分类问题
在前面所有的算法都是以二分类为例的,一方面因为二分类便于原理的理解,另一方面多分类问题都是基于二分类进行的。其实多分类问题包括单个标签的多个类别问题以及多个标签的多分类问题。
单标签的多分类问题是指仅有一个标签,有多个类别,比如图片辨识中猫、狗、大象等分类,多标签多类别是指有多个标签,比如猫本身有一个标签,同时猫与植物相比,又带有动物的标签,这就属于一个多标签的分类问题。
在此主要说的是单标签多分类的任务,多标签分类比较复杂,后面会对多标签分类问题进行简单的介绍,并附上相关博客,后面遇到要解决的问题再进行学习。
对于单标签的分类问题,前面在LogisticRegression中讲到了softmax,其实,对于多分类问题,通常可以转化为二分类问题来解决多分类问题,常见的策略包括:OVO(一对一策略)、OVR(一对多策略)以及MVM(多对多策略)。
OVO(一对一策略)
OVO是指将样本类别进行两两组合,单后组合后分别进行训练,这样就训练出n(n-1)/2个分类器,然后最终对于一个新样本,分别输入到这些分类器当中,最终进行投票得到结果,如图所示:
那么对于一个新的样本,其投票方式如下:
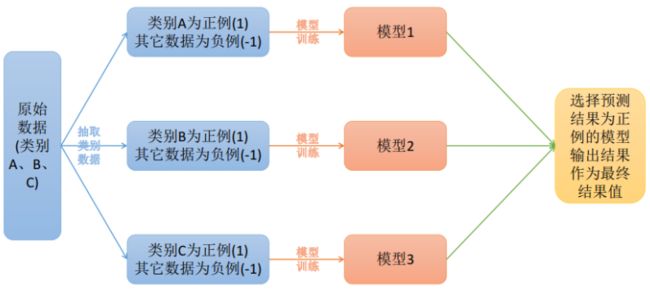
OVR(一对多策略)
在一对多中,将所有类别仅看做类别X和其他,即分别选出每个类别后,将剩余样本作为一类,然后按照二分类进行训练。在测试时,若仅有一个分类器预测为正类,则对应的类别标记作为最终分类结果。若有多个分类器预测为正类,则通常考虑各分类器的预测置信度,选择预测置信度最大的类别标记作为分类结果。训练如图所示:
对于样本的预测:
MVM(多对多策略)
MVM策略是将样本中一部分类别选出来作为正类,一部分类别作为负类,MVM的正反类选取不能随意选取,必须有一定的特殊设计,最常见的技术是纠错码机制(ECOC),将编码的思想引入类别拆分,并尽可能在解码过程中具有容错性。
纠错码机制分为两步:
(1)编码:
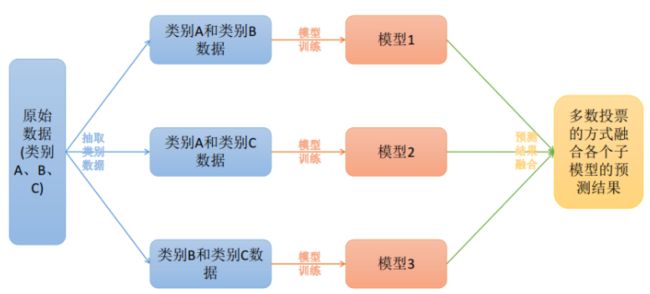
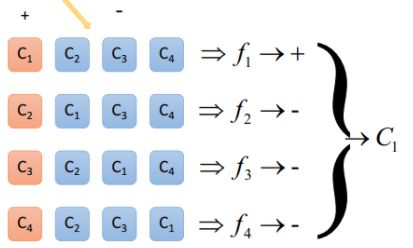
将样本的K个类别进行M次划分,每一次划分将一部分类别分为正类,一部分分为负类,然后训练一个模型出来,这样就能构建出M个模型;同时一个类别也被划分了M次;
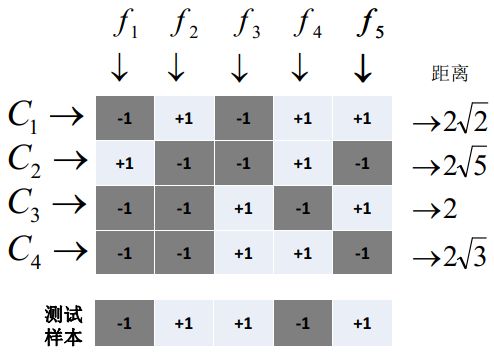
(2)解码阶段
将待测样本分别带进M个模型中,就会产生出M个结果,然后计算M个结果与上面每个类的被划分M次的结果之间的距离,距离与待测类别距离较近的记为待测样本所属类别。
具体原理如图所示:
3.多标签多类别问题
多标签问题每一个样本包含多个标签,如特征标签中,一个物品存在多个标签,尤其对于文本挖掘用途广泛,如一篇新闻可能属于政治,也可能属于经济类。那么多标签主要问题是:
(1)标签数量的不确定性,并非所有数据的标签数量是固定不变的,有的样本可能仅有1个标签,但有的可能有成百上千个;
(2)标签之间存在相互依赖关系,比如有的样本要确定了前一个标签,才能确定后面的标签,如一篇文章是属于议论文还是散文,如果属于散文,其第二个标签是属于抒情散文还是叙事散文;
(3)通常多标签的样本数据对于标签的获取比较困难,通常标签需要人工标注或机器标注,但是标签体系过于庞大时,有时这项工作很难进行。
那么解决多标签问题通常有两种思路:
(1)基于问题转化的方法,就是把多标签问题转化为我们可以解决的单标签问题,这种通常无法解决标签之间的依赖问题;
(2)基于算法适应的方法,使用现有算法,对算法进行扩展,改进算法,使其能够适应多标签数据,如MLKNN、rank-SVM等算法,这些方法中有些能够解决依赖问题,但有些也无法解决标签之间的依赖问题。
具体多标签问题暂时这里不再说明,附一篇有关多标签问题解决的综述文章:https://www.cnblogs.com/cxf-zzj/p/10049613.html
后边涉及到这类问题,再详细进行了解和学习。
参考文献:
机器学习:多分类及多标签分类
多标签分类(multi-label classification)综述
本部分主要是对前面提到一些后续补充的内容进行一个总结和补充,主要是关于正则化和多分类的问题,其中多分类仅针对单标签多分类问题进行了叙述,后面有涉及到多标签多分类再进行了解和学习。