机器学习和深度学习之数学基础-线性代数 第二节 矩阵的概念及运算

本文为原创文章，欢迎转载，但请务必注明出处。

上文介绍了线性映射，而与线性映射直接相关的就是矩阵，它决定了线性映射的结果，这里介绍矩阵的一些基本概念和运算。包括矩阵的转置、逆、特征值与特征向量、投影、正交矩阵、对称矩阵、正定矩阵、内积和外积、SVD、二次型等基本概念。本文主要参考Garrett Thomas(2018)，Marc Peter Deisenroth(2018)，Strang(2003)，José Miguel Figueroa-O’Farrill， Isaiah Lankham(UCD, MAT67,2012)等教授的相关讲座和教材。

1、 矩阵的转置

矩阵转置的定义很简单，矩阵的转置就是将矩阵的行变为列，即 A∈ℝm×n A ∈ R m × n ， 那么转置 A⊤∈ℝn×m A ⊤ ∈ R n × m ，且 (A⊤)ij=Aji ( A ⊤ ) i j = A j i 。

转置的性质：

• (A⊤)⊤=A ( A ⊤ ) ⊤ = A
• (A+B)⊤=A⊤+B⊤ ( A + B ) ⊤ = A ⊤ + B ⊤
• (αA)⊤=αA⊤ ( α A ) ⊤ = α A ⊤
• (AB)⊤=B⊤A⊤ ( A B ) ⊤ = B ⊤ A ⊤

若 A⊤=A A ⊤ = A ， 那么 A A 称为对称矩阵(symmetric)。任何一个矩阵都可以是一个对称矩阵和反对称矩阵(antisymmetric)的和：

A=12(A+A⊤)+12(A−A⊤) A = 1 2 ( A + A ⊤ ) + 1 2 ( A − A ⊤ )

其中， 12(A+A⊤) 1 2 ( A + A ⊤ ) 是对称矩阵， 12(A−A⊤) 1 2 ( A − A ⊤ ) 是反对称矩阵。

2、可逆矩阵(invertible matrix)

一个方阵 A∈ℝn×n A ∈ R n × n 可逆当且仅当存在一个方阵 B∈ℝn×n B ∈ R n × n 使得

AB=I A B = I

其中 I∈ℝn×n I ∈ R n × n 为单位矩阵。那么方阵 B B 为方阵 A A 的逆矩阵，记作 A−1 A − 1 。

如果矩阵 A∈ℝn×n A ∈ R n × n ，那么下面的说法等价：

• A A 可逆
• A A 不是奇异矩阵(non-singular)
• 行列式 det(A)≠0 d e t ( A ) ≠ 0
• A A 满秩，即 rank(A=n) r a n k ( A = n )
• Ax=0 A x = 0 只有唯一解： x=0 x = 0
• A A 的零空间只有零向量： { 0} { 0 } ，即 null(A)=0 n u l l ( A ) = 0
• A A 的列向量线性无关
• A A 的列向量的张成是整个 ℝn R n 空间。
• A A 的列向量构成 ℝn R n 的一个基向量集
• 存在方阵 B∈ℝn×n B ∈ R n × n 使得 AB=I=BA A B = I = B A .
• 转置 A⊤ A ⊤ 是可逆矩阵，于是，矩阵 A A 的行向量是线性无关的，张成是 ℝn R n 空间，同时构成了 ℝn R n 的一个基向量集。
• A A 不存在值为0的特征值。
• A A 可以表示为有限个初等矩阵的乘积。
• A A 有左逆矩阵（即 BA=I B A = I ）和 右逆矩阵(即 AC=I A C = I )，且 B=C=A−1 B = C = A − 1 。

可逆矩阵 A A 的一些重要性质：

• (A−1)−1=A ( A − 1 ) − 1 = A ;
• (αA)−1=α−1A−1 ( α A ) − 1 = α − 1 A − 1 ，这里实数标量 α≠0 α ≠ 0
• (A⊤)−1=(A−1)⊤ ( A ⊤ ) − 1 = ( A − 1 ) ⊤
• (AB)−1=B−1A−1 ( A B ) − 1 = B − 1 A − 1 ，其中 B∈ℝn×n B ∈ R n × n 是可逆矩阵。 更一般情况，如果方阵 A1,...Ak A 1 , . . . A k 可逆，那么 (A1...Ak)−1=A−1k...A−11 ( A 1 . . . A k ) − 1 = A k − 1 . . . A 1 − 1 .
• det(A−1)=(det(A))−1 d e t ( A − 1 ) = ( d e t ( A ) ) − 1

如果方阵 A A 的逆矩阵就是它自身，即 A=A−1 A = A − 1 ， 那么有 A2=I A 2 = I ，这是方阵 A A 就叫对合矩阵(involutory matrix)。

3、矩阵的列空间(columnspace)和行空间(rowspace)， 矩阵的秩(rank)

矩阵 A∈ℝm×n A ∈ R m × n 的列空间(columnspace)是指其列向量(看成是 ℝm R m 中的向量)的张成； 类似的，行空间(rowspace)是指其行向量(看成是 ℝn R n 中的向量)的张成。

矩阵 A A 的列空间等于由矩阵 A A 导致的线性映射 ℝn→ℝm R n → R m 的值域, 即 range(A) r a n g e ( A ) 。

矩阵 A∈ℝm×n A ∈ R m × n 的列秩是矩阵 A A 的线性无关的列向量的最大数量。类似地，行秩是矩阵 A A 的线性无关的行向量的最大数量。 矩阵的列秩和行秩总是相等的，因此它们可以简单地称作矩阵 A A 的秩，通常表示为 r(A) r ( A ) 或 rank(A) r a n k ( A ) 。

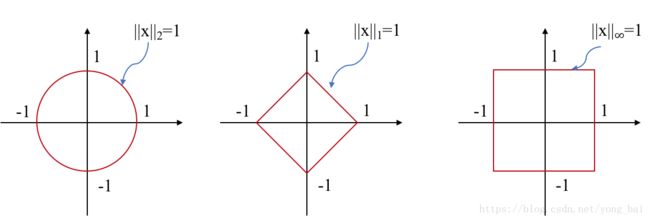
4、范数(norm)和内积(inner product)

4.1、范数(norm)

范数(norm)是对欧氏空间距离的一般描述。在实数向量空间 V V 的一个范数是一个函数 ‖⋅‖:V→ℝ ‖ ⋅ ‖ : V → R ，并且满足：

• ‖x‖≥0 ‖ x ‖ ≥ 0 ， 当且仅当 x=0 x = 0 等号成立；
• ‖αx‖=|α|‖x‖ ‖ α x ‖ = | α | ‖ x ‖
• ‖x+y‖≤‖x‖+‖y‖ ‖ x + y ‖ ≤ ‖ x ‖ + ‖ y ‖ （三角不等式）

注意在 V V 上的任何范数都会引出一个在 V V 上的距离度量： d(x,y)=‖x−y‖ d ( x , y ) = ‖ x − y ‖

常用的范数包括：

‖x‖1=∑i=1n|xi| ‖ x ‖ 1 = ∑ i = 1 n | x i |

‖x‖2=∑i=1nx2i‾‾‾‾‾‾⎷ ‖ x ‖ 2 = ∑ i = 1 n x i 2

‖x‖p=(∑i=1n|xi|p)1p,(p≥1) ‖ x ‖ p = ( ∑ i = 1 n | x i | p ) 1 p , ( p ≥ 1 )

‖x‖∞=max1≤i≤n|xi| ‖ x ‖ ∞ = m a x 1 ≤ i ≤ n | x i |

图一，不同范数在二维平面的示例

4.2、内积(inner product)

在实数向量空间 V V 的一个内积是一个函数 ⟨⋅⟩:V×V→ℝ ⟨ ⋅ ⟩ : V × V → R ，并且满足：

• ⟨x,x⟩≥0 ⟨ x , x ⟩ ≥ 0 ，当且仅当 x=0 x = 0 等号成立
• ⟨x+y,z⟩=⟨x,z⟩+⟨y,z⟩ ⟨ x + y , z ⟩ = ⟨ x , z ⟩ + ⟨ y , z ⟩ ， ⟨αx,y⟩=α⟨x,y⟩ ⟨ α x , y ⟩ = α ⟨ x , y ⟩
• ⟨x,y⟩=⟨y,x⟩ ⟨ x , y ⟩ = ⟨ y , x ⟩

另外，对于向量的2-范数，有

‖x‖=⟨x,x⟩‾‾‾‾‾√ ‖ x ‖ = ⟨ x , x ⟩

当 ⟨x,y⟩=0 ⟨ x , y ⟩ = 0 时， 那么在同一向量空间中的非零向量 x x 和 y y 正交 (orthogonal, 垂直，记为 x⊥y x ⊥ y )。 如果 x x 和 y y 还是单位长度，即 ‖x‖=‖y‖=1 ‖ x ‖ = ‖ y ‖ = 1 ，那么向量 x x 和 y y 称为是标准正交的(orthonormal)。

向量正交的几何解释，如下图二，假设向量 x x 和 y y 的夹角是 θ θ ，那么由于：

⟨x,y⟩=‖x‖‖y‖cos(θ) ⟨ x , y ⟩ = ‖ x ‖ ‖ y ‖ c o s ( θ )

当夹角 θ=π/2 θ = π / 2 （即垂直）时， cos(θ)=0 c o s ( θ ) = 0 ，所以有 ⟨x,y⟩=0 ⟨ x , y ⟩ = 0 。

图二，空间中两个向量之间的夹角

通常内积被记为：

⟨x,y⟩=∑i=1nxiyi=x⊤y ⟨ x , y ⟩ = ∑ i = 1 n x i y i = x ⊤ y

在空间 ℝn R n 上， 内积被称为点积(dot product)， 记为 x⋅y x ⋅ y 。

（毕氏定理，Pythagorean Theorem）如果 x⊥y x ⊥ y ， 那么 ‖x+y‖2=‖x‖2+‖y‖2 ‖ x + y ‖ 2 = ‖ x ‖ 2 + ‖ y ‖ 2 。

（柯西-施瓦茨不等式，Cauchy-Schwarz inequality）: |⟨x,y⟩|≤‖x‖‖y‖ | ⟨ x , y ⟩ | ≤ ‖ x ‖ ‖ y ‖

5、投影(projection)

5.1、点到直线的投影

考虑下图中的两个向量 u,v∈ℝ2 u , v ∈ R 2 ，如何将向量 u u 投影到向量 v v 上呢？

图三，一个向量投影到另一个向量

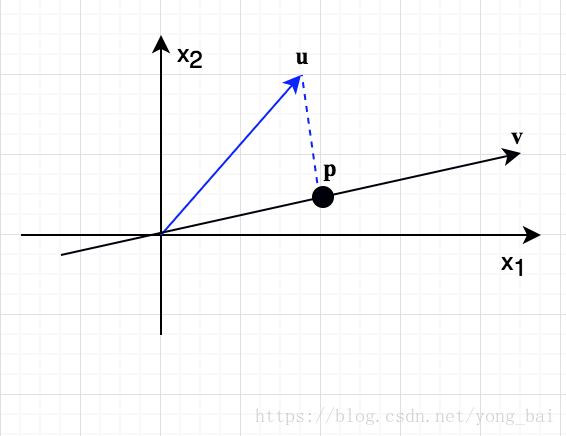
假设 u u 投影到向量 v v 上的最近的点是 p p ，即 p p 点（将向量看成一个空间的一点）是一条通过 u u 点的直线并与向量 v v 所在直线垂直且相交的点。这时，如果用向量 p p 来近似向量 u u ，那么误差为 e=u−p e = u − p 。下面来求 u u 在向量 v v 上的投影 p p 。因为 p p 与 向量 v v 在同一直线上，那么设 p=αv p = α v ，由于 v v 与 e e 垂直，那么有 v⊤e=0 v ⊤ e = 0 ， 即

v⊤(u−αv)=0αv⊤v=v⊤uα=v⊤uv⊤v v ⊤ ( u − α v ) = 0 α v ⊤ v = v ⊤ u α = v ⊤ u v ⊤ v

于是，

p=αv=v⊤uv⊤vv p = α v = v ⊤ u v ⊤ v v

5.2、投影矩阵(projection matrix)

下面介绍用投影矩阵描述上述的投影，即 p=Pu p = P u 。由于：

p=vv⊤uv⊤v=vv⊤v⊤vu=Pu p = v v ⊤ u v ⊤ v = v v ⊤ v ⊤ v u = P u

所以, 投影矩阵

P=vv⊤v⊤v P = v v ⊤ v ⊤ v

投影矩阵具有如下一些性质：

• 投影矩阵 P P 的列空间是有向量 v v 张成的，因为对于任何一个向量 u u ， Pu P u 都是位于由向量 v v 所决定的直线上。
• 秩 rank(P)=1 r a n k ( P ) = 1 ；
• 对称矩阵: P⊤=P P ⊤ = P ;
• P2=P P 2 = P 。

P P 叫做正交(与向量所在直线正交)投影矩阵。

5.3、点到平面的投影

在 ℝ3 R 3 中，如何将向量 u u 投影到平面上距离 u u 最近的 p p 点呢？

首先假设 a1 a 1 和 a2 a 2 是平面上的两个基向量，那么该平面就是矩阵 A=[a1  a2] A = [ a 1     a 2 ] 的列空间（即两个基向量张成所构成的空间)。

基于上面的假设，那么平面里的任意一点（或任意一个向量） p p 都可以由平面的两个基向量线性表示，即 p=α1a1+α2a2=Aα p = α 1 a 1 + α 2 a 2 = A α 。 我们需要求得向量 α=(α1,α2) α = ( α 1 , α 2 ) ，也就是说我们要在平面上找一个 p p ，使得 u u 到 p p 的距离最近（即垂直）。如图四所示。

图四，向量映射到平面。 a1 a 1 和 a2 a 2 是平面里的两个基向量，那么平面里的任意向量都可以由这两个向量的线性组合得到，这就是向量 p=α1a1+α2a2=Aα p = α 1 a 1 + α 2 a 2 = A α 的原因

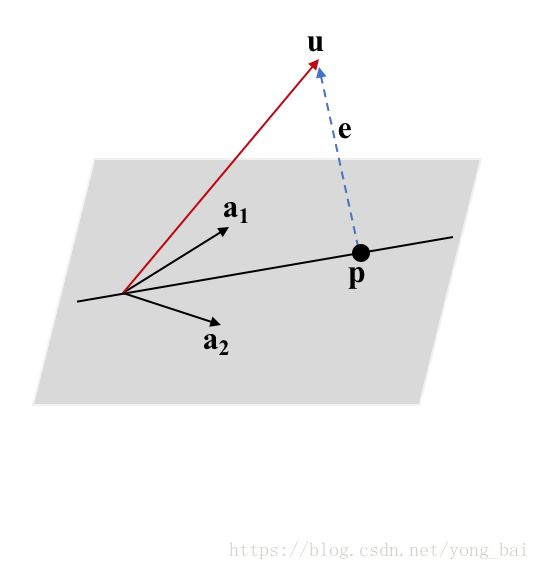
类似“点到直线投影”的方法，点 u u 到平面上一点 p p 的误差向量为 e=u−p=u−Aα e = u − p = u − A α 。也就是说，要使得误差 e e 最小，只需要 u u 垂直投影到平面上，而 p p 就是 e e 与平面相交的点。

由于 e e 与平面垂直，那么 e e 就与平面上所有的向量或直线垂直，最简单的就是 e e 与平面的两个基向量 a1 a 1 和 a2 a 2 都垂直，所以有：

a⊤1(u−Aα)=0a⊤2(u−Aα)=0 a 1 ⊤ ( u − A α ) = 0 a 2 ⊤ ( u − A α ) = 0

用矩阵表示就是： A⊤(u−Aα)=0 A ⊤ ( u − A α ) = 0 。

还有就是， e=u−Aα e = u − A α 是在 A⊤ A ⊤ 的零空间里，所以 e e 也是在 A A 的左零空间里(left nullspace)。我们知道所有在 A A 的左零空间里的向量都是与 A A 的列空间垂直的。这也从另一个方面验证了上述计算。

由于 A⊤(u−Aα)=0 A ⊤ ( u − A α ) = 0 ， 所以

A⊤Aα=A⊤u A ⊤ A α = A ⊤ u

如果是映射到直线，那么 A⊤A A ⊤ A 就是一个标量数值，但是如果是映射到平面， A⊤A A ⊤ A 变成了一个方阵(square matrix)。所以这里不再是除以 v⊤v v ⊤ v ，而是乘以 A⊤A A ⊤ A 的逆 (A⊤A)−1 ( A ⊤ A ) − 1 。

所以（对于 n n 维空间也是一样）有

α=(A⊤A)−1A⊤up=Aα=A(A⊤A)−1A⊤uP=A(A⊤A)−1A⊤ α = ( A ⊤ A ) − 1 A ⊤ u p = A α = A ( A ⊤ A ) − 1 A ⊤ u P = A ( A ⊤ A ) − 1 A ⊤

这里，仍然有 P⊤=P,P2=P P ⊤ = P , P 2 = P 。

P P 叫做正交(这里是与平面正交)投影矩阵。如果 A A 中的列向量之间两两相互正交，且向量长度为1（标准正交向量），那么 A⊤A=I A ⊤ A = I ，所以有 P=A(A⊤A)−1A⊤=AA⊤ P = A ( A ⊤ A ) − 1 A ⊤ = A A ⊤ 。（注意，这个结论的矩阵 A A 必须是标准正交的列向量组成）。

5.4、从投影的视角看线性回归

线性回归问题：给定 m m 个数据对 {(xi,yi)}mi=1 { ( x i , y i ) } i = 1 m ，其中 xi∈ℝn,yi∈ℝ x i ∈ R n , y i ∈ R ， 目标是找到一点直线 ŷ =θ⊤x y ^ = θ ⊤ x 能“最好的”拟合这些点使得损失最小。为了找到这样的直线，问题变成了根据给定的 m m 个数据点求向量参数 θ θ 。

现在以矩阵来表示： X∈ℝm×n X ∈ R m × n ， y∈ℝm y ∈ R m 。 假设这些数据是由真实的 y=Xθ+ϵ y = X θ + ϵ ， 其中 ϵ ϵ 是高斯白噪声。我们的目标就是求 ŷ =Xθ y ^ = X θ ，使得真实的 y y 与模型预测的 ŷ  y ^ 误差最小。

假设平面是两个向量 x1 x 1 和 x2 x 2 的张成（即 x1 x 1 和 x2 x 2 是平面的两个基向量）， y y 是平面外的一个点，我们记作 X=[x1  x2] X = [ x 1     x 2 ] 。 由于我们定义了 ŷ =Xθ y ^ = X θ ， 那就说明 ŷ  y ^ 是平面两个基向量 x1 x 1 和 x2 x 2 的线性组合，也就是说， ŷ  y ^ 也在平面上。我们求向量参数 θ θ ，使得平面外的 y y 与平面上的 ŷ  y ^ 距离最近，那么就是说 ŷ  y ^ 是通过向量 y y 的直线垂直于平面的交点。根据上面4.3的结论，有（如图五所示）

图五，从投影的视角看线性回归

X⊤(y−Xθ)=0 X ⊤ ( y − X θ ) = 0

于是，有

θ=(X⊤X)−1X⊤y θ = ( X ⊤ X ) − 1 X ⊤ y

6、特征值(eigenvalue)和特征向量(eigenvector)

凡是涉及到特征值和特征向量时，矩阵首先必须是方阵， 即 A∈ℝn×n A ∈ R n × n 。

如果方阵 A A 作用于一个非零向量 x∈ℝn x ∈ R n ，得到的结果其实只是简单的对向量 x x 进行拉伸或收缩(scaled) λ λ 个单位，即经过方阵 A A 的作用（或叫做线性变换）后向量 x x 的方向不变只是长度变化了（这个特性也叫线性不变性），那么这个特殊的向量 x x 就是方阵 A A 的一个特征向量， λ λ 则是该特征向量对应的特征值，即

Ax=λx A x = λ x

特征向量不包括零向量（ 0 0 ）。

假设方阵 A A 的一个特征向量为 x x ，对应的特征值是 λ λ ，下面列出一些重要的结论：
- 对于任意的实数 γ∈ℝ γ ∈ R ，那么方阵 A+γI A + γ I 的特征向量仍然是 x x ， 对应的特征值变为 λ+γ λ + γ ；
- 如果方阵 A A 可逆，那么方阵 A−1 A − 1 的特征向量仍然是 x x 对应的特征值为 λ−1 λ − 1 ；
- 对于任意的整数 k∈ℤ k ∈ Z ，有 Akx=λkx A k x = λ k x ，（这里 定义 A0=I A 0 = I ）。

后面会详细介绍特征值和特征向量的应用。

7、矩阵的迹(trace)

在谈到矩阵的迹(trace)的时候一般也是针对的方阵。一个方阵的迹是该方阵上的对角线上元素的和，即

tr(A)=∑i=1nAii t r ( A ) = ∑ i = 1 n A i i

迹的一些重要的性质：

• tr(A+B)=tr(A)+tr(B) t r ( A + B ) = t r ( A ) + t r ( B ) ；
• tr(αA)=αtr(A) t r ( α A ) = α t r ( A ) ，这里 α∈ℝ α ∈ R ；
• tr(A⊤)=tr(A) t r ( A ⊤ ) = t r ( A )
• tr(ABCD)=tr(BCDA)=tr(CDBA)=tr(DABC) t r ( A B C D ) = t r ( B C D A ) = t r ( C D B A ) = t r ( D A B C ) 。

另外，方阵的迹等于方阵的所有特征值的和，即

tr(A)=∑iλi(A) t r ( A ) = ∑ i λ i ( A )

8、行列式(determinant)

行列式（方阵才有行列式）的定义在这里就不在介绍，这里列出一些重要性质：

• det(I)=1 d e t ( I ) = 1
• det(A⊤)=det(A) d e t ( A ⊤ ) = d e t ( A )
• det(AB)=det(A)det(B) d e t ( A B ) = d e t ( A ) d e t ( B )
• det(A−1)=det(A)−1 d e t ( A − 1 ) = d e t ( A ) − 1
• det(αA)=αndet(A) d e t ( α A ) = α n d e t ( A )

另外，方阵的行列式等于该方阵的所有特征值的乘积，即

det(A)=∏iλi(A) d e t ( A ) = ∏ i λ i ( A )

从几何意义的角度，在二维平面上，行列式的绝对值等于由矩阵的两个向量（列向量或行向量都可以）为临边所围成的平行四边形的面积；如果是3维空间，那么行列式的绝对值等于由矩阵的三个向量（列向量或行向量都可以）为临边所围成的平行四边体的体积，以此类推。

图六，二维平面中行列式的几何意义

9、正交矩阵(Orthogonal matrices)

如果方阵 Q∈ℝn×n Q ∈ R n × n 的列两两标准正交(pairwise orthonormal)，那么 Q Q 称为正交矩阵， 即

Q⊤Q=QQ⊤=I Q ⊤ Q = Q Q ⊤ = I

也就是说，正交矩阵的转置等于它的逆，即 Q⊤=Q−1 Q ⊤ = Q − 1 。正交矩阵作用于任何向量（即与向量相乘，矩阵和向量相乘也可以看成根据矩阵对向量进行线性变换）保留了向量的内积结果(即内积结果不受正交矩阵相乘的影响)，即

(Qx)⊤(Qy)=x⊤Q⊤Qy=x⊤Iy=x⊤y ( Q x ) ⊤ ( Q y ) = x ⊤ Q ⊤ Q y = x ⊤ I y = x ⊤ y

一个直接的结果就是正交矩阵保留了2-范数的结果：

‖Qx‖2=(Qx)⊤(Qx)‾‾‾‾‾‾‾‾‾‾√=x⊤x‾‾‾‾√=‖x‖2 ‖ Q x ‖ 2 = ( Q x ) ⊤ ( Q x ) = x ⊤ x = ‖ x ‖ 2

上面的结果因此说明了正交矩阵与向量相乘可以看成是一个保留了向量长度的线性变换，但是方向有可能针对向量的原点进行了旋转或翻转。

10、对称矩阵(symmetric matrices)

如果方阵 A∈ℝn×n A ∈ R n × n 的转置就是它本身，那么方阵 A A 就称为对称矩阵，即 A=A⊤ A = A ⊤ 。
以下介绍一个重要的定理：

矩阵质谱定理(Spectral Theorem)：如果方阵 A∈ℝn×n A ∈ R n × n 是对称矩阵，那么在 ℝn R n 空间中存在由方阵 A A 的特征向量组成的标准正交基(orthonormal basis)。

这个定理的直接应用就是对对称矩阵的因子化(factorization)，也就是常说的矩阵的特征分解(eigen decomposition)或谱分解(spectral decomposition)。假设对称方阵 A A 的特征向量（也就是方阵 A A 对应空间 ℝn R n 的标准正交基)为 q1,...,qn q 1 , . . . , q n ，对应的特征值为 λ1,...,λn λ 1 , . . . , λ n 。假设正交矩阵 Q Q 的列就是 q1,...,qn q 1 , . . . , q n ，对角矩阵 Λ=diag(λ1,...,λn) Λ = d i a g ( λ 1 , . . . , λ n ) 。根据这些假设，所以对所有的 i i 有 Aqi=λiqi A q i = λ i q i ，于是用矩阵表示就是

AQ=QΛ A Q = Q Λ

上式右乘 Q⊤ Q ⊤ ，就可以可以得到矩阵分解:

A=QΛQ⊤ A = Q Λ Q ⊤

11、瑞利熵(Rayleigh quotients)

如果方阵 A∈ℝn×n A ∈ R n × n 是对称矩阵，那么表达式 x⊤Ax x ⊤ A x 称为二次型 (quadratic form)。

瑞利熵(Rayleigh quotients，见下面的等式)将一个对称矩阵的二次型与该对称矩阵的特征值联系了起来：

A(x)=x⊤Axx⊤x R A ( x ) = x ⊤ A x x ⊤ x

一些瑞利熵的重要性质：
- 标量不变性：对于任意非零向量 x≠0 x ≠ 0 和任意非零实数标量 α≠0 α ≠ 0 ， 有 A(x)=A(αx) R A ( x ) = R A ( α x )
- 如果 x x 是方阵 A A 的特征向量，对应的特征值是 λ λ ， 有 A(x)=λ R A ( x ) = λ 。

下面两个性质对求解某些问题也很重要，这些性质说明对称矩阵 A A 的瑞利熵的计算结果是介于 A A 的最小和最大特征值之间的：

• 对于任意向量 x x ，如果其长度为1（即 ‖x‖2=1 ‖ x ‖ 2 = 1 ），那么有
  
  λmin(A)≤x⊤Ax≤λmax(A) λ m i n ( A ) ≤ x ⊤ A x ≤ λ m a x ( A )
  
  当其仅当向量 x x 为其对应的特征向量时，等号成立。

• （瑞丽熵的最小最大定理，min-max theorem）：对于任意的非0向量 x x ，有
  

  λmin(A)≤A(x)≤λmax(A) λ m i n ( A ) ≤ R A ( x ) ≤ λ m a x ( A )
  
  当其仅当向量 x x 为其对应的特征向量时，等号成立。

  后面我们会介绍瑞丽熵的应用及其与拉格朗日算子求极值的例子。

12、正定（或半正定）矩阵 (Positive (semi-)definite matrices)

对于对称矩阵 A A ，如果对于所有的向量 x∈ℝn x ∈ R n ，都有 x⊤Ax≥0 x ⊤ A x ≥ 0 ， 记作 A⪰0 A ⪰ 0 ，那么对称矩阵 A A 称为半正定矩阵。如果对于所有的非零向量 x∈ℝn x ∈ R n ，都有 x⊤Ax>0 x ⊤ A x > 0 ， 记作 A≻0 A ≻ 0 ，那么对称矩阵 A A 称为正定矩阵。

下面的一些性质与其特征值有关：

• 一个对称矩阵是半正定矩阵当且仅当它的所有特征值都是非负的；一个对称矩阵是正定矩阵当且仅当它的所有特征值都是正的。
• 假设任意矩阵 A∈ℝm×n A ∈ R m × n ，那么 A⊤A A ⊤ A 是半正定矩阵。 如果 A A 的零空间只有 0 0 向量， 即 null(A)={ 0} n u l l ( A ) = { 0 } ， 那么 A A 是正定矩阵（ null(A)={ 0} n u l l ( A ) = { 0 } 说明只要向量 x∈ℝn x ∈ R n 是非零向量，那么就有 Ax≠0 A x ≠ 0 ）。
• 如果 A A 是半正定矩阵，对于任意 ϵ>0 ϵ > 0 ，那么 A+ϵI A + ϵ I 是正定矩阵。

12.1、正定二次型的几何表示（The geometry of positive definite quadratic forms）

一个理解二次型的有用方法就是通过观察他们的几何水平集(the geometry of their level set)。一个函数的水平集或等高线(isocontour)是一组输入的集合，对于这些输入，函数都产生一个相同的值或结果，如函数 f f 的 c c -等高线是 { x∈dom  f:f(x)=c} { x ∈ d o m     f : f ( x ) = c } 。

考虑一个特殊情况 f(x)=x⊤Ax f ( x ) = x ⊤ A x ，其中 A A 是正定矩阵。由于 A A 是正定矩阵，那么它有唯一的矩阵平方根 A12=QΛ12Q A 1 2 = Q Λ 1 2 Q ，其中 QΛQ Q Λ Q 是 A A 的特征分解， Λ12=diag(λ1‾‾√,...,λn‾‾√) Λ 1 2 = d i a g ( λ 1 , . . . , λ n ) 。很容易看出 A12 A 1 2 是正定矩阵（因为它的所有特征值都是大于0的），而且有 A12A12=A A 1 2 A 1 2 = A 。 给定一个实数 c>0 c > 0 ， 那么函数 f f 的 c c -等高线就是一组 x∈ℝn x ∈ R n ，且满足：

c=x⊤Ax=x⊤A12A12x=‖‖A12x‖‖22 c = x ⊤ A x = x ⊤ A 1 2 A 1 2 x = ‖ A 1 2 x ‖ 2 2

上式中， A12 A 1 2 是对称矩阵。设 z=A12x z = A 1 2 x ，那么有 ‖z‖2=c√ ‖ z ‖ 2 = c 。 这就是说向量的值 z z 是位于半径为 c√ c 的圆上。进一步，我们加入参数使 z=c√ẑ  z = c z ^ ，其中 ‖z‖2=1 ‖ z ‖ 2 = 1 ，那么由于 A−12=QΛ−12Q⊤ A − 1 2 = Q Λ − 1 2 Q ⊤ ，所以有，

x=A−12z=QΛ−12Q⊤c√ẑ =c√QΛ−12z̃  x = A − 1 2 z = Q Λ − 1 2 Q ⊤ c z ^ = c Q Λ − 1 2 z ~

其中 z̃ =Q⊤ẑ  z ~ = Q ⊤ z ^ ， 因为 Q Q 是正交矩阵，所以 z̃  z ~ 也是满足 ‖z̃ ‖2=1 ‖ z ~ ‖ 2 = 1 。使用这种参数化的方式可以得到结果集 { x∈ℝn:f(x)=c} { x ∈ R n : f ( x ) = c } 是在可逆的线性映射 x=c√QΛ−12z̃  x = c Q Λ − 1 2 z ~ 的单位圆影像(image of the unit sphere） { z̃ ∈ℝn:‖z̃ ‖2} { z ~ ∈ R n : ‖ z ~ ‖ 2 } 。( 矩阵的影像(image of matrix)是指该矩阵的张成(Think of it (image of the matrix) as what vectors you can get from applying the linear transformation or multiplying the matrix by a vector, from wiki)) 。

通过这些运算可以看出，经过一系列的线性变换后可以很清楚的理解函数 f f 的 c c -等高线是如何得到的：首先开始于一个单位圆（或单位球面)，然后对每个坐标轴 i i 拉伸或压缩 对应的 λ12i λ i 1 2 个单位，由此得到一个轴对齐的椭球(an axis-aligned ellipsoid)。椭球的轴长度与正定矩阵 A A 的特征值的平方根倒数成正比。所以，特征值越大，对应的椭球的轴的长度就越小，反之亦然。

然后这个轴对齐的椭球通过矩阵 Q Q 进行了一个刚性变换（rigid transform, 即保留长度和角度，例如旋转或反射（rotation/reflection）等)这个变换的结果就是椭圆的轴不在沿着原来的坐标轴方向，而是沿着相应的特征向量方向。为了说明这点，假设有一个单位向量 ei∈ℝn e i ∈ R n ，有 [ei]j=δij [ e i ] j = δ i j 。在变换之前的空间，这个向量指向原坐标轴方向，其长度与 λ12i λ i 1 2 成正比。但是，进过刚性变化 Q Q 后，该向量指向的方向变成了相应的特征向量 qi q i 的方向，因为：

Qei=∑j=1n[ei]jqj=qi Q e i = ∑ j = 1 n [ e i ] j q j = q i

这里我们使用了matrix-vector product identity。

总结： f(x)=x⊤Ax f ( x ) = x ⊤ A x 的等高线是椭球，椭球的轴是指向了 A A 的特征向量方向，这些轴的半径是与相应的特征值的平方根倒数成正比的。

13、奇异值分解(Singular value decomposition)

任意矩阵 A∈ℝm×n A ∈ R m × n 都有一个SVD (即使该矩阵不是方阵)。

SVD的矩阵分解如下：

A=UΣV⊤ A = U Σ V ⊤

其中 U∈ℝm×m U ∈ R m × m 和 V∈ℝn×