1.7 非平衡数据的处理方法大全

非平衡数据的处理

前言

在实际应用中，读者可能会碰到一种比较头疼的问题，那就是分类问题中类别型的因变量可能存在严重的偏倚，即类别之间的比例严重失调。所谓的不平衡指的是不同类别的样本量差异非常大，或者少数样本代表了业务的关键数据(少量样本更重要)，需要对少量样本的模式有很好的学习。样本类别分布不平衡主要出现在分类相关的建模问题上。

样本类别分布不均衡从数据规模上可以分为大数据分布不均衡和小数据分布不均衡两种:

• 大数据分布不均衡——整体数据规模较大，某类别样本占比较小。例如拥有1000万条记录的数据集中.其中占比5万条的少数分类样本便于属于这种情况。
• 小数据分布不均衡——整体数据规模小,则某类别样本的数量也少,这种情况下，由于少量祥本数太少，很难提取特征进行有/无监督算法学习，此时属于严重的小数据样本分布不均衡。例如拥有100个样本,20个A类祥本，80个B类样本。

如欺诈问题中，欺诈类观测在样本集中毕竟占少数；客户流失问题中，忠实的客户往往也是占很少一部分；在某营销活动的响应问题中，真正参与活动的客户也同样只是少部分。 如果数据存在严重的不平衡，预测得出的结论往往也是有偏的，即分类结果会偏向于较多观测的类。

典型场景

• CTR预估:广告点击率，通常只有百分之几，点击的样本占比非常少，大量的未点击样本
• 异常检测:比如恶意刷单、黄牛订单、信用卡欺诈、电力窃电、设备故障等，这些数据样本所占的比例通常是整体样本中很少的一部分，以信用卡欺诈为例，刷实体信用卡的欺诈比例一般都在0.1%以内。
• 罕见事件的分析:罕见事件分析与异常事件的区别在于异常检测通常都有是预先定义好的规则和逻辑，并且大多数异常事件都对会企业运营造成负面影响，因此针对异常事件的检测和预防非常重要;但军见事件则无法预判，并且也没有明显的积极和消极影响倾向

对于这种问题该如何处理呢？

最简单粗暴的办法就是构造1:1的数据，要么将多的那一类砍掉一部分（欠采样、下采样），要么将少的那一类进行Bootstrap抽样（过采样）。但这样做会存在问题，对于第一种方法，砍掉的数据会导致某些隐含信息的丢失；而第二种方法中，有放回的抽样形成的简单复制，又会使模型产生过拟合。

不平衡案例

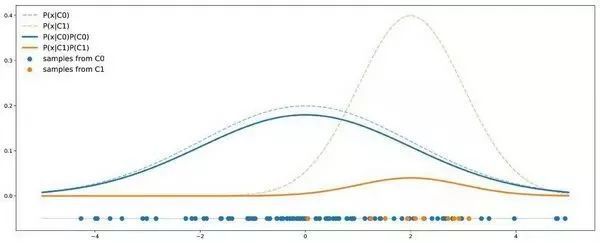
在解决问题之前，我们要更好地理解问题。为此我们考虑一个非常简单的例子。假设我们有两个类：C0 和 C1，其中 C0 的点遵循均值为 0、方差为 4 的一维高斯分布;C1 的点遵循均值为 2 、方差为 1 的一维高斯分布。假设数据集中 90% 的点来自 C0，其余 10% 来自 C1。下图是包含 50 个点的数据集按照上述假设的理论分布情况：

$$不平衡案例图示$$

虚线表示每个类的概率密度，实线加入了对数据比例的考量。

在这个例子中，我们可以看到 C0 的曲线总是在 C1 曲线之上，因此对于任意给定点，它出自 C0 类的概率总是大于出自 C1 类的概率。用贝叶斯公式来表示，即：
$$\mathbb{P}(C0\mid x)=\frac{\mathbb{P}(x\mid C0)\mathbb{P}(C0)}{\mathbb{P}(x)}>\frac{\mathbb{P}(x\mid C1)\mathbb{P}(C1)}{\mathbb{P}(x)}=\mathbb{P}(C1\mid x)$$
在这里我们可以清楚地看到先验概率的影响，以及它如何导致一个类比另一个类更容易发生的情况。这就意味着，即使从理论层面来看，只有当分类器每次判断结果都是 C0 时准确率才会最大。所以假如分类器的目标就是获得最大准确率，那么我们根本就不用训练，直接全部判为 C0 即可。

关于可分离性

在前面的例子中，我们可以观察到两个类似乎不能很好地分离开(彼此相距不远)。但是，数据不平衡不代表两个类无法很好地分离。例如，我们仍假设数据集中 C0、C1 的比例分别为 90% 和 10%;但 C0 遵循均值为 0 、方差为 4 的一维高斯分布、C1 遵循均值为 10 、方差为 1 的一维高斯分布。如下图所示：

在这个例子中，如果均值差别足够大，即使不平衡类也可以分离开来。

在这里我们看到，与前一种情况相反，C0 曲线并不总是高于 C1 曲线，因此有些点出自 C1 类的概率就会高于出自 C0 的概率。在这种情况下，两个类分离得足够开，足以补偿不平衡，分类器不一定总是得到 C0 的结果。

理论最小误差概率

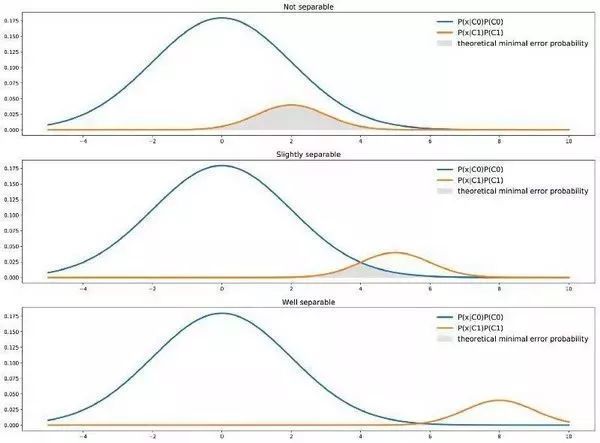
我们应当明白这一点，分类器具有理论意义上的最小误差概率。对于单特征二分类分类器，用图表来看的话，理论最小误差概率是由两条曲线最小值下的面积给出的：

$$两个类在不同分离度下的理论最小误差$$
我们可以用公式的形式来表示。实际上，从理论的角度来看，最好的分类器将从两个类中选择点 $x$ 最有可能属于的类。这自然就意味着对于给定的点 $x$，最好的理论误差概率由这两个类可能性较小的一个给出，即
$$\mathbb{P}(\text{ wrong }\mid x)=\min (\mathbb{P}(C0\mid x),\mathbb{P}(C1\mid x))=\frac{\min (\mathbb{P}(x\mid C0)\mathbb{P}(C0),\mathbb{P}(x\mid C1)\mathbb{P}(C1))}{\mathbb{P}(x)}$$
然后我们可以对全体进行积分，得到总误差概率：
$$\mathbb{P}(\text{ wrong })={\int }_{\mathbb{R}}\mathbb{P}(\text{ wrong }\mid x)\mathbb{P}(x)dx={\int }_{\mathbb{R}}\min (\mathbb{P}(x\mid C0)\mathbb{P}(C0),\mathbb{P}(x\mid C1)\mathbb{P}(C1))dx$$
即上图中两条曲线最小值下区域的面积。

重新处理数据集并不总是解决方案

面对不平衡数据集，我们的第一个反应可能会认为这个数据没有代表现实。如果这是正确的，也就是说，实际数据应该是(或几乎是)平衡的，但由于我们采集数据时的方法问题造成数据存在比例偏差。因此我们必须尝试收集更具代表性的数据。

下采样、过采样和 组合采样

这三种方法通常在训练分类器之前使用以平衡数据集。

1 、欠采样

欠采样(也叫下采样、under sampling,US)是通过减少多数样本的大小来平衡数据集，当数据量足够时就该使用此方法。通过保存所有少数类样本，并在多数样本类别中随机选择与少数类别样本相等数量的样本，可以检索平衡的新数据集以进一步建模。通过欠采样，在保留少量样本的同时，会丢失多数类样本中的一些信息。经过欠采样，样本总量在减少。

from sklearn.datasets import make_classification
from collections import Counter
X, y = make_classification(n_samples=5000, n_features=2, n_informative=2,
                           n_redundant=0, n_repeated=0, n_classes=3,
                           n_clusters_per_class=1,
                           weights=[0.01, 0.05, 0.94],
                           class_sep=0.8, random_state=0)
Counter(y)


Out[1]: Counter({
     0: 64, 1: 262, 2: 4674})

1.1 原型选择(prototype selection)

随机删除

随机地删除一些多量样本，使少量样本和多量样本数量达到均衡

1. 分别确定样本集中多量样本数 $N_{maj}$ 和少量样本数 $N_{\min };$
2. 确定采样样本集中多量样本与少量样本比值 $N_{\text{ratio }}$;
3. 以少量样本数为基准，确定多量样本采样总数 $N_{\text{sample }}=N_{\text{ratio }}\ast N_{\min }$
4. 以 $N_{\text{sample }}$ 为限，对多量样本进行随机抽样。

python中random.sample()方法可以随机地从指定列表中提取出N个不同的元素，列表的维数没有限制。

import tensorflow as tf
import numpy as np
import random
seed_idx = list(np.arange(0,100,1))
sample_idx = random.sample(seed_idx,40)

与原型生成不同的是, 原型选择算法是直接从原始数据集中进行抽取. 抽取的方法大概可以分为两类: (i) 控制下采样技术；(ii) 采样下的清洁技术

第一类的方法可以由用户指定下采样抽取的子集中样本的数量;

RandomUnderSampler函数是一种快速并十分简单的方式来平衡各个类别的数据: 随机选取数据的子集.

from imblearn.under_sampling import RandomUnderSampler
under_sampling = RandomUnderSampler(random_state=0)
X_resampled, y_resampled = under_sampling.fit_sample(X, y)

print(sorted(Counter(y_resampled).items()))

Out[2]:
[(0, 64), (1, 64), (2, 64)]

import numpy as np
np.vstack({
     tuple(row) for row in X_resampled}).shape

Out[3]:
(192, 2)

很明显, 使用默认参数的时候, 采用的是不重复采样;通过设置RandomUnderSampler中的replacement=True参数, 可以实现自助法(boostrap)抽样.通过设置RandomUnderSampler中的rratio参数,可以设置数据采样比例

under_sampling=RandomUnderSampler(random_state=1,replacement=True) #采用随机欠采样（下采样）
X_resampled, y_resampled = under_sampling.fit_sample(X, y)

print(sorted(Counter(y_resampled).items()))
print(np.vstack({
     tuple(row) for row in X_resampled}).shape)

Out[4]:
[(0, 64), (1, 64), (2, 64)]
(185, 2)

NearMiss函数则添加了一些启发式(heuristic)的规则来选择样本, 通过设定version参数来实现三种启发式的规则.

下面通过一个例子来说明这三个启发式的选择样本的规则, 首先我们假设正样本是需要下采样的(多数类样本), 负样本是少数类的样本.

NearMiss-1: 选择离N个近邻的负样本的平均距离最小的正样本;

NearMiss-2: 选择离N个负样本最远的平均距离最小的正样本;

NearMiss-3: 是一个两段式的算法. 首先, 对于每一个负样本, 保留它们的M个近邻样本; 接着, 那些到N个近邻样本平均距离最大的正样本将被选择.

from imblearn.under_sampling import NearMiss
nm1 = NearMiss( version=1)
X_resampled_nm1, y_resampled = nm1.fit_sample(X, y)

print(sorted(Counter(y_resampled).items()))
print(np.vstack({
     tuple(row) for row in X_resampled}).shape)

[(0, 64), (1, 64), (2, 64)]
(185, 2)

第二类方法则不接受这种用户的干预.

使用最近的邻居编辑数据集

EditedNearestNeighbours这种方法应用最近邻算法来编辑(edit)数据集, 找出那些与邻居不太友好的样本然后移除. 对于每一个要进行下采样的样本, 那些不满足一些准则的样本将会被移除; 他们的绝大多数(kind_sel='mode')或者全部(kind_sel='all')的近邻样本都属于同一个类, 这些样本会被保留在数据集中.

print(sorted(Counter(y).items()))

from imblearn.under_sampling import EditedNearestNeighbours
enn = EditedNearestNeighbours(random_state=0)
X_resampled, y_resampled = enn.fit_sample(X, y)

print(sorted(Counter(y_resampled).items()))

Out:
[(0, 64), (1, 262), (2, 4674)]
[(0, 64), (1, 213), (2, 4568)]

在此基础上, 延伸出了RepeatedEditedNearestNeighbours算法, 重复基础的EditedNearestNeighbours算法多次.

from imblearn.under_sampling import RepeatedEditedNearestNeighbours
renn = RepeatedEditedNearestNeighbours(random_state=0)
X_resampled, y_resampled = renn.fit_sample(X, y)

print(sorted(Counter(y_resampled).items()))

Out:
[(0, 64), (1, 208), (2, 4551)]

与RepeatedEditedNearestNeighbours算法不同的是, ALLKNN算法在进行每次迭代的时候, 最近邻的数量都在增加.

from imblearn.under_sampling import AllKNN
allknn = AllKNN(random_state=0)
X_resampled, y_resampled = allknn.fit_sample(X, y)

print(sorted(Counter(y_resampled).items()))

Out:
[(0, 64), (1, 220), (2, 4601)]

浓缩最近邻和派生算法

CondensedNearestNeighbour 使用1近邻的方法来进行迭代, 来判断一个样本是应该保留还是剔除, 具体的实现步骤如下:

1. 集合C: 所有的少数类样本;
2. 选择一个多数类样本(需要下采样)加入集合C, 其他的这类样本放入集合S;
3. 使用集合S训练一个1-NN的分类器, 对集合S中的样本进行分类;
4. 将集合S中错分的样本加入集合C;
5. 重复上述过程, 直到没有样本再加入到集合C.

from imblearn.under_sampling import CondensedNearestNeighbour
cnn = CondensedNearestNeighbour(random_state=0)
X_resampled, y_resampled = cnn.fit_sample(X, y)

print sorted(Counter(y_resampled).items())
Out[39]:
[(0, 64), (1, 24), (2, 115

显然, CondensedNearestNeighbour方法对噪音数据是很敏感的, 也容易加入噪音数据到集合C中.

因此, OneSidedSelection 函数使用 TomekLinks 方法来剔除噪声数据(多数类样本).

from imblearn.under_sampling import OneSidedSelection
oss = OneSidedSelection(random_state=0)
X_resampled, y_resampled = oss.fit_sample(X, y)

print(sorted(Counter(y_resampled).items()))
Out[39]:
[(0, 64), (1, 174), (2, 4403)]

NeighbourhoodCleaningRule 算法主要关注如何清洗数据而不是筛选(considering)他们. 因此, 该算法将使用

EditedNearestNeighbours和 3-NN分类器结果拒绝的样本之间的并集.

from imblearn.under_sampling import NeighbourhoodCleaningRule
ncr = NeighbourhoodCleaningRule(random_state=0)
X_resampled, y_resampled = ncr.fit_sample(X, y)

print sorted(Counter(y_resampled).items())
Out[39]:
[(0, 64), (1, 234), (2, 4666)]

Instance hardness threshold

InstanceHardnessThreshold是一种很特殊的方法, 是在数据上运用一种分类器, 然后将概率低于阈值的样本剔除掉.

from sklearn.linear_model import LogisticRegression
from imblearn.under_sampling import InstanceHardnessThreshold
iht = InstanceHardnessThreshold(random_state=0,
                                estimator=LogisticRegression())
X_resampled, y_resampled = iht.fit_sample(X, y)

print(sorted(Counter(y_resampled).items()))
Out[39]:
[(0, 64), (1, 64), (2, 64)]

1.2 原型生成(prototype generation)

给定数据集S, 原型生成算法将生成一个子集S’, 其中|S’| < |S|, 但是子集并非来自于原始数据集. 意思就是说: 原型生成方法将减少数据集的样本数量, S’,的样本是由原始数据集生成的, 而不是直接来源于原始数据集.具体做法如下∶

1. 以少量样本总数出发，确定均衡后多量样本总数 $N_{maj}$
2. 多量样本出发，利用K-means算法随机的计算K个多量样本的中心;
3. 认为K-means的中心点可以代表该样本簇的特性，以该中心点 $s^{\prime }$ 代表该样本簇；

4. 重复2、3两步 $N_{maj}$ 次，生成新的多量样本集合 $S^{\prime }=s_1^{\prime },s_2^{\prime },\dots s_{N_{maj}}^{\prime }$ 并且 $S^{\prime }\notin S$

ClusterCentroids函数实现了上述功能: 每一个类别的样本都会用K-Means算法的中心点来进行合成, 而不是随机从原始样本进行抽取.

from imblearn.under_sampling import ClusterCentroids

under_sampling = ClusterCentroids(random_state=0)
X_resampled, y_resampled = under_sampling.fit_sample(X, y)

print(sorted(Counter(y_resampled).items()))

Out:
[(0, 64), (1, 64), (2, 64)]

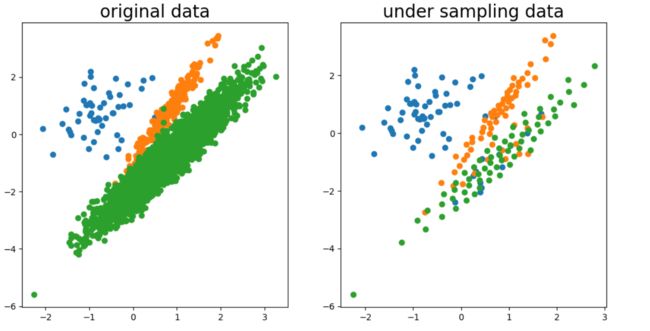
import  matplotlib.pyplot as plt


plt.figure(figsize=(12, 6), dpi=100)
# 为每个类的样本创建散点图
for class_value in range(3):
    plt.subplot(1, 2, 1)
    # 获取此类的示例的行索引
    row_ix = np.where(y == class_value)
    # 创建这些样本的散布
    plt.scatter(X[row_ix, 0], X[row_ix, 1])
    plt.title("original data", fontdict={
     'size': 20})

for class_value in range(3):
    plt.subplot(1, 2, 2)
    # 获取此类的示例的行索引
    row_ix = np.where(y_resampled == class_value)
    # 创建这些样本的散布
    plt.scatter(X_resampled[row_ix, 0], X_resampled[row_ix, 1])
    plt.title("under sampling data", fontdict={
     'size': 20})
# 绘制散点图
plt.show()

利用原型生成算法完成数据均衡后，样本整体分布没有变化

1.2. 过采样

相反，当数据量不足时就应该使用过采样(也叫上采样、over-sampling)，它尝试通过增加少数样本的数量来平衡数据集，而不是去除多数类别的样本的数量。通过使用重复、自举或合成少数类过采样等方法（SMOTE）来生成新的稀有样品。

最直接的方法是简单复制少数类样本形成多条记录，这种方法的缺点是如果样本特征少而可能导致过拟合的问题。

经过改进的过抽样方法通过在少数类中加入随机噪声、干扰数据或通过一定规则产生新的合成样本，对应的算法会在后面介绍。

朴素随机过采样

针对不平衡数据, 最简单的一种方法就是生成少数类的样本, 这其中最基本的一种方法就是: 从少数类的样本中进行随机采样来增加新的样本, RandomOverSampler 函数就能实现上述的功能.

from imblearn.over_sampling import RandomOverSampler

ros = RandomOverSampler(random_state=0)
X_resampled, y_resampled = ros.fit_sample(X, y)
sorted(Counter(y_resampled).items())

Out:
[(0, 4674), (1, 4674), (2, 4674)]

以上就是通过简单的随机采样少数类的样本, 使得每类样本的比例为1:1:1.

SMOTE算法

为了解决数据的非平衡问题，2002年Chawla提出了SMOTE算法， 即合成少数过采样技术，它是基于随机过采样算法的一种改进方案。该技术是目前处理非平衡数据的常用手段，并受到学术界和工业界的一致 认同，接下来简单描述一下该算法的理论思想。

SMOTE算法的基本思想就是对少数类别样本进行分析和模拟，并将人工模拟的新样本添加到数据集中，进而使原始数据中的类别不再严重失衡。该算法的模拟过程采用了KNN技术，模拟生成新样本的步骤如下：

• （1）采样最邻近算法，计算出每个少数类样本的$K$个近邻。

• （2）从$K$个近邻中随机挑选$N$个样本进行随机线性插值。

• （3）构造新的少数类样本。

• （4）将新样本与原数据合成，产生新的训练集。

为了使读者理解SMOTE算法实现新样本的模拟过程，可以参考图3和人工新样本的生成过程。

$$图3:SMOTE算法示意图$$

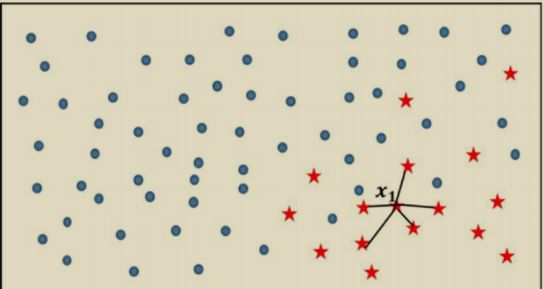
如图3所示，实心圆点代表的样本数量要明显多于五角星代表的样本点，如果使用SMOTE算法模拟增加少类别的样本点，则需要经过如下几个步骤：

（1）利用KNN算法，选择离样本点 $x_1$​ 最近的$K$个同类样本点（不妨最近邻为5）。

（2）从最近的$K$个同类样本点中，随机挑选$M$个样本点（不妨设M 为2），$M$的选择依赖于最终所希望的平衡率。

（3）对于每一个随机选中的样本点，构造新的样本点。新样本点的构造需要使用下方的公式:
$$x_{\text{new}}=x_i+\lambda \times \left(x_j-x_i\right),j=1,2,\dots ,M$$
其中， $x_i$ 表示少数类别中的一个样本点（如图3中五角星所代表 的 $x_1$ 样本 $);x_j$ 表示从K近邻中随机挑选的样本点 $j$; $\lambda =rand(0,1)$​ 表示生成 0~1的随机数。

假设图3中样本点$x_1$的观测值为(2,3,10,7)，从图3中的5个近邻随机挑选两个样本点，它们的观测值分别为(1,1,5,8)和(2,1,7,6)，由此得到的两个新样本点为:
$$\begin{array}{c}{x}_{\text{new}}=(2,3,10,7)+0.3\times ((1,1,5,8)-(2,3,10,7))=(1.7,2.4,8.5,7.3)\\ x_{\text{new}2}=(2,3,10,7)+0.26\times ((2,1,7,6)-(2,3,10,7))=(2,2.48,9.22,6.74)\end{array}$$
（4）重复步骤（1）、（2）和（3），通过迭代少数类别中的每一个样本$x_i$，最终将原始的少数类别样本量扩大为理想的比例。

由于SMOTE算法构建样本时，是随机的 进行样本点的组 合和 $\lambda$​ 参数设置, 因此会 有以下2个问题:

• 在进行少量样本构造时，只是简单的在同类近邻之间插值，并没有考虑少数类样本周围多数类样本的分布情况。对于少量样本比较稀疏的区域，采用与少量样本比较密集的区域相同的概率进行构建，会使构建的样本可能更接近于边界;

  例如图4，蓝色的点是少量样本稀疏的点。我们第一次选了这个蓝色的$x_{i1},x_{j1}$，然后我们去构造了$x_{new,1}$啊，这个点对吧，然后我们第二个点就是这个$x_{i2},x_{j2}$，然后构造出了$x_{new,2}$​。这样的问题在于并没有考虑少数类样本周围多数类样本的分布情况，就是这两个蓝色的点，你在构造新的样本的时候，并没有考虑到这些新样本的情况。

• 当样本维度过高时，样本在空间上的分布会稀疏，由此可能使构建的样本无法代表少量样本的特征。

$$图4:SMOTE数据点的构建$$
通过SMOTE算法实现过采样的技术并不是太难，读者可以根据上面的步骤自定义一个抽样函数。当然，读者也可以借助于imblearn模块，并利用其子模块over_sampling中的SMOTE“类”实现新样本的生成。有关该“类”的语法和参数含义如下：

SMOTE(ratio='auto', random_state=None, k_neighbors=5, m_neighbors=10, 
out_step=0.5, kind='regular', svm_estimator=None, n_jobs=1) 

• ratio：用于指定重抽样的比例，如果指定字符型的值，可以是’minority’（表示对少数类别的样本进行抽样）、‘majority’（表示对多数类别的样本进行抽样）、‘not minority’（表示采用欠采样方法）、‘all’（表示采用过采样方法），默认为’auto’，等同 于’all’和’not minority’。如果指定字典型的值，其中键为各个类别标签，值为类别下的样本量。
• random_state：用于指定随机数生成器的种子，默认为None，表示使用默认的随机数生成器。
• k_neighbors：指定近邻个数，默认为5个。
• m_neighbors：指定从近邻样本中随机挑选的样本个数，默认为10个。
• kind：用于指定SMOTE算法在生成新样本时所使用的选项，默认为’regular’，表示对少数类别的样本进行随机采样，也可以是’borderline1’ ‘borderline2’和’svm’。
• svm_estimator：用于指定SVM分类器，默认为sklearn.svm.SVC，该参数的目的是利用支持向量机分类器生成支持向量，然后生成新的少数类别的样本。
• n_jobs：用于指定SMOTE算法在过采样时所需的CPU数量，默认为1表示仅使用1个CPU运行算法，即不使用并行运算功能。

SMOTE: 对于少数类样本a, 随机选择一个最近邻的样本b, 然后从a与b的连线上随机选取一个点c作为新的少数类样本; 不会区分容易和难分类的样本。

ADASYN: 关注的是在那些基于K最近邻分类器被错误分类的原始样本附近生成新的少数类样本

from imblearn.over_sampling import SMOTE, ADASYN

X_resampled_smote, y_resampled_smote = SMOTE().fit_sample(X, y)
print(sorted(Counter(y_resampled_smote).items()))


X_resampled_adasyn, y_resampled_adasyn = ADASYN().fit_sample(X, y)
print(sorted(Counter(y_resampled_adasyn).items()))

out:
[(0, 4674), (1, 4674), (2, 4674)]
[(0, 4673), (1, 4662), (2, 4674)]

SMOTE的变体

SMOTE可能会连接内嵌点和离群点，而ADASYN可能只关注离群点，在这两种情况下，都可能导致次优决策函数。针对上述问题,衍生出SMOTEBoost、Borderline-SMOTE、Kmeans-SMOTE等。这些方法关注最优决策函数边界附近的样本，并生成与最近邻类相反方向的样本。

• SMOTEBoost把SMOTE算法和Boost算法结合，在每一轮分类学习过程中增加对少数类的梯本的权重，使得基学习器(base learner)能够更好地关注到少数类样本。
• Borderline-SMOTE在构造样本时考虑少量样本周围的样本分布，选择少量样本集合(DANGER集合)——其邻居节点既有多量样本也有少量样本，且多量样本数不大于少量样本的点来构造新样本。
• Kmeans-SMOTE包括聚类、过滤和过采样三步。利用Kmeans算法完成聚类后，进行样本簇过滤，在每个样本簇内利用SMOTE算法构建新样本。

SMOTEBoost的实现

from collections import Counter

import numpy as np
from sklearn.base import is_regressor
from sklearn.ensemble import AdaBoostClassifier
from sklearn.ensemble.forest import BaseForest
from sklearn.neighbors import NearestNeighbors
from sklearn.preprocessing import normalize
from sklearn.tree.tree import BaseDecisionTree
from sklearn.utils import check_random_state
from sklearn.utils import check_X_y

class SMOTEBoost(AdaBoostClassifier):
    """Implementation of SMOTEBoost.
    SMOTEBoost introduces data sampling into the AdaBoost algorithm by
    oversampling the minority class using SMOTE on each boosting iteration [1].
    This implementation inherits methods from the scikit-learn 
    AdaBoostClassifier class, only modifying the `fit` method.
    Parameters
    ----------
    n_samples : int, optional (default=100)
        Number of new synthetic samples per boosting step.
    k_neighbors : int, optional (default=5)
        Number of nearest neighbors.
    base_estimator : object, optional (default=DecisionTreeClassifier)
        The base estimator from which the boosted ensemble is built.
        Support for sample weighting is required, as well as proper `classes_`
        and `n_classes_` attributes.
    n_estimators : int, optional (default=50)
        The maximum number of estimators at which boosting is terminated.
        In case of perfect fit, the learning procedure is stopped early.
    learning_rate : float, optional (default=1.)
        Learning rate shrinks the contribution of each classifier by
        ``learning_rate``. There is a trade-off between ``learning_rate`` and
        ``n_estimators``.
    algorithm : {'SAMME', 'SAMME.R'}, optional (default='SAMME.R')
        If 'SAMME.R' then use the SAMME.R real boosting algorithm.
        ``base_estimator`` must support calculation of class probabilities.
        If 'SAMME' then use the SAMME discrete boosting algorithm.
        The SAMME.R algorithm typically converges faster than SAMME,
        achieving a lower test error with fewer boosting iterations.
    random_state : int or None, optional (default=None)
        If int, random_state is the seed used by the random number generator.
        If None, the random number generator is the RandomState instance used
        by np.random.
    References
    ----------
    .. [1] N. V. Chawla, A. Lazarevic, L. O. Hall, and K. W. Bowyer.
           "SMOTEBoost: Improving Prediction of the Minority Class in
           Boosting." European Conference on Principles of Data Mining and
           Knowledge Discovery (PKDD), 2003.
    """

    def __init__(self,
                 n_samples=100,
                 k_neighbors=5,
                 base_estimator=None,
                 n_estimators=50,
                 learning_rate=1.,
                 algorithm='SAMME.R',
                 random_state=None):

        self.n_samples = n_samples
        self.algorithm = algorithm
        self.smote = SMOTE(k_neighbors=k_neighbors,
                           random_state=random_state)

        super(SMOTEBoost, self).__init__(
            base_estimator=base_estimator,
            n_estimators=n_estimators,
            learning_rate=learning_rate,
            random_state=random_state)

    def fit(self, X, y, sample_weight=None, minority_target=None):
        """Build a boosted classifier/regressor from the training set (X, y),
        performing SMOTE during each boosting step.
        Parameters
        ----------
        X : {array-like, sparse matrix} of shape = [n_samples, n_features]
            The training input samples. Sparse matrix can be CSC, CSR, COO,
            DOK, or LIL. COO, DOK, and LIL are converted to CSR. The dtype is
            forced to DTYPE from tree._tree if the base classifier of this
            ensemble weighted boosting classifier is a tree or forest.
        y : array-like of shape = [n_samples]
            The target values (class labels in classification, real numbers in
            regression).
        sample_weight : array-like of shape = [n_samples], optional
            Sample weights. If None, the sample weights are initialized to
            1 / n_samples.
        minority_target : int
            Minority class label.
        Returns
        -------
        self : object
            Returns self.
        Notes
        -----
        Based on the scikit-learn v0.18 AdaBoostClassifier and
        BaseWeightBoosting `fit` methods.
        """
        # Check that algorithm is supported.
        if self.algorithm not in ('SAMME', 'SAMME.R'):
            raise ValueError("algorithm %s is not supported" % self.algorithm)

        # Check parameters.
        if self.learning_rate <= 0:
            raise ValueError("learning_rate must be greater than zero")

        if (self.base_estimator is None or
                isinstance(self.base_estimator, (BaseDecisionTree,
                                                 BaseForest))):
            DTYPE = np.float64  # from fast_dict.pxd
            dtype = DTYPE
            accept_sparse = 'csc'
        else:
            dtype = None
            accept_sparse = ['csr', 'csc']

        X, y = check_X_y(X, y, accept_sparse=accept_sparse, dtype=dtype,
                         y_numeric=is_regressor(self))

        if sample_weight is None:
            # Initialize weights to 1 / n_samples.
            sample_weight = np.empty(X.shape[0], dtype=np.float64)
            sample_weight[:] = 1. / X.shape[0]
        else:
            sample_weight = check_array(sample_weight, ensure_2d=False)
            # Normalize existing weights.
            sample_weight = sample_weight / sample_weight.sum(dtype=np.float64)

            # Check that the sample weights sum is positive.
            if sample_weight.sum() <= 0:
                raise ValueError(
                    "Attempting to fit with a non-positive "
                    "weighted number of samples.")

        if minority_target is None:
            # Determine the minority class label.
            stats_c_ = Counter(y)
            maj_c_ = max(stats_c_, key=stats_c_.get)
            min_c_ = min(stats_c_, key=stats_c_.get)
            self.minority_target = min_c_
        else:
            self.minority_target = minority_target

        # Check parameters.
        self._validate_estimator()

        # Clear any previous fit results.
        self.estimators_ = []
        self.estimator_weights_ = np.zeros(self.n_estimators, dtype=np.float64)
        self.estimator_errors_ = np.ones(self.n_estimators, dtype=np.float64)

        random_state = check_random_state(self.random_state)

        for iboost in range(self.n_estimators):
            # SMOTE step.
            X_min = X[np.where(y == self.minority_target)]
            self.smote.fit(X_min)
            X_syn = self.smote.sample(self.n_samples)
            y_syn = np.full(X_syn.shape[0], fill_value=self.minority_target,
                            dtype=np.int64)

            # Normalize synthetic sample weights based on current training set.
            sample_weight_syn = np.empty(X_syn.shape[0], dtype=np.float64)
            sample_weight_syn[:] = 1. / X.shape[0]

            # Combine the original and synthetic samples.
            X = np.vstack((X, X_syn))
            y = np.append(y, y_syn)

            # Combine the weights.
            sample_weight = \
                np.append(sample_weight, sample_weight_syn).reshape(-1, 1)
            sample_weight = \
                np.squeeze(normalize(sample_weight, axis=0, norm='l1'))

            # X, y, sample_weight = shuffle(X, y, sample_weight,
            #                              random_state=random_state)

            # Boosting step.
            sample_weight, estimator_weight, estimator_error = self._boost(
                iboost,
                X, y,
                sample_weight,
                random_state)

            # Early termination.
            if sample_weight is None:
                break

            self.estimator_weights_[iboost] = estimator_weight
            self.estimator_errors_[iboost] = estimator_error

            # Stop if error is zero.
            if estimator_error == 0:
                break

            sample_weight_sum = np.sum(sample_weight)

            # Stop if the sum of sample weights has become non-positive.
            if sample_weight_sum <= 0:
                break

            if iboost < self.n_estimators - 1:
                # Normalize.
                sample_weight /= sample_weight_sum

        return self

ros = SMOTEBoost(n_estimators=100, n_samples=300)
ros.fit(xtrain_glove, ytrain)
y_pred = ros.predict(xvalid_glove)

BorderlineSMOTE ， SVMSMOTE 和KMeansSMOTE :

from imblearn.over_sampling import BorderlineSMOTE ,KMeansSMOTE
X_resampled, y_resampled = BorderlineSMOTE().fit_resample(X, y)
print(sorted(Counter(y_resampled).items()))

X_resampled, y_resampled = KMeansSMOTE().fit_resample(X, y)
print(sorted(Counter(y_resampled).items()))

通过比较不同算法得到的样本构造,可得以下结论:

1. 利用样本构建的方法，可以得到新的少量样本;
2. 利用不同算法构建的新样本在数量和分布上不同，其中利用SMOTE算法构建的新样本，由于没有考虑原始样本分布情况，构建的新样本会受到“噪声”点的影响。同样ASASYN算法只考虑了分布密度而未考虑样本分布，构建的新样本也会受到“噪声”点的影响。Borderline-SMOTE算法由于考虑了样本的分布，构建的新样本能够比较好的避免“噪声”点的影响。Kmeans-SMOTE算法由于要去寻找簇后再构建新样本，可构建的新样本数量受限。

注:"噪声”点对应类别上属于少量样本，但是分布上比较靠近边界或者与多量样本混为一起。

1.3. 组合采样

组合不同的重采样数据集

生成通用模型的最简单方法是使用更多的数据。问题是，开箱即用的分类器，如逻辑回归或机森随林，倾向于通过丢弃稀有样例来推广。一个简单的最佳实现是建立n个模型，使用少数类的所有样本和数量充足类别的n个不同样本。假如您想要组合10个模型，需要少数类1000例，随机抽取10.000例多数类的样本。然后，只需将10000个样本分成10个块，训练出10个不同的模型。

如果您有大量数据，那么这种方法很简单，完美地实现水平扩展，因此您可以在不同的集群节点上训练和运行模型。集合模型也趋于一般化，使得该方法容易处理。

用不同比例重新采样

以前的方法可以通过少数类和多数类之间的比例进行微调。最好的比例在很大程度上取决于所使用的数据和模型。但是，不是在整体中以相同的比例训练所有模型，合并不同的比例值得尝试。 所以如果训练了10个模型，对一个模型比例为1：1（少数：多数），另一个1：3甚至是2：1的模型是有意义的。 根据使用的模型可以影响一个类获得的权重。

总结

注意到下采样和过采样这两种方法相比而言，都没有绝对的优势。这两种方法的应用取决于它适用的用例和数据集本身。另外将过采样和下采样结合起来使用也是成功的。

简单来说：

• 欠采样：从样本较多的类中再抽取，仅保留这些样本点的一部分;
• 过采样：复制少数类中的一些点，以增加其基数;
• 生成合成数据：从少数类创建新的合成点，以增加其基数。

所有这些方法目的只有一个：重新平衡(部分或全部)数据集。但是我们应该重新平衡数据集来获得数据量相同的两个类吗?或者样本较多的类应该保持最大的代表性吗?如果是这样，我们应以什么样的比例来重新平衡呢?

$$不同程度的多数类欠采样对模型决策的影响$$
当使用重采样方法(例如从 C0 获得的数据多于从 C1 获得的数据)时，我们在训练过程向分类器显示了两个类的错误比例。以这种方式学得的分类器在未来实际测试数据上得到的准确率甚至比在未改变数据集上训练的分类器准确率还低。实际上，类的真实比例对于分类新的点非常重要，而这一信息在重新采样数据集时被丢失了。

因此，即使不完全拒绝这些方法，我们也应当谨慎使用它们：有目的地选择新的比例可以导出一些相关的方法，但如果没有进一步考虑问题的实质而只是将类进行重新平衡，那么这个过程可能毫无意义。总结来讲，当我们采用重采样的方法修改数据集时，我们正在改变事实，因此需要小心并记住这对分类器输出结果意味着什么。

Bagging

Bagging的算法原理如下：

用不同比例重新采样的数据进行Bagging训练：

\1. 对两类样本选取 N 组不同比例的数据进行训练并测试，得出模型预测的准确率：

P={ Pi | i=1,2,…N }

\2. 对上述各模型的准确率进行归一化处理，得到新的权重分布：

Ω={ ωi | i=1,2,…N }

其中：
$${\omega }_i=\frac{p_i}{{\sum }_{i=0}^N{p}_i}$$
\3. 按权重分布 Ω 组合多个模型，作为最终的训练器：

$\bullet$ 对于分类任务：
$$\text{ Model }=\underset{i}{\mathrm{argmax}}\sum _{y_i=i}{\omega }_i$$
$\bullet$ 对于分类任务：
$$\text{ Model }=\sum _{i=1}^N{\omega }_i{y}_i$$
在之前的例子中，从总体中可替换的抽取10个bootstrap样本，每个样本包含200个观测值。每个样本都与原始数据不相同，但是与原始数据的分布和可变性相似。很多机器学习算法都可以用来训练这10个bootstrap样本，如逻辑回归、神经网络、决策树等，得到10个不同的分类器C1，C2.….C10。将这10个分类器集合成一个复合分类器。这种集合算法结合了多个单独的分类器的结果，可以得到一个更好的复合分类器。Bagging算法提升了机器学习算法的稳定性和准确性，并且解决了过拟合问题。在有噪点的数据环境中，bagging比boosting表现更加优异。

在集成分类器中, 装袋方法(Bagging)在不同的随机选取的数据集上建立了多个估计量. 在scikit-learn中这个分类器叫做BaggingClassifier.

from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix
from sklearn.ensemble import BaggingClassifier
from sklearn.tree import DecisionTreeClassifier

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
bc = BaggingClassifier(base_estimator=DecisionTreeClassifier(),
                       random_state=0)
bc.fit(X_train, y_train) 

y_pred = bc.predict(X_test)
confusion_matrix(y_test, y_pred)

#out
array([[   9,    1,    2],
       [   0,   54,    5],
       [   1,    6, 1172]], dtype=int64)

imblearn.ensemble.``BalancedBaggingClassifier 具有额外平衡的袋装分类器。

Bagging的这个实现类似于scikit-learn的实现。它包括一个额外的步骤，在适当的时间使用给定的采样器来平衡训练集。

该分类器可作为实现精确平衡套袋、大致平衡套袋、过度套袋、间断性套袋等各种方法的基础。

from collections import Counter
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix
from imblearn.ensemble import BalancedBaggingClassifier 

print('Original dataset shape %s' % Counter(y))
X_train, X_test, y_train, y_test = train_test_split(X, y,
                                                    random_state=0)
bbc = BalancedBaggingClassifier(random_state=42)
bbc.fit(X_train, y_train) 
y_pred = bbc.predict(X_test)
print(confusion_matrix(y_test, y_pred))

#out
Original dataset shape Counter({
     2: 4674, 1: 262, 0: 64})
[[   9    1    2]
 [   0   55    4]
 [  49   50 1080]]

添加额外特征

重采样数据集(修改类比例)是好是坏取决于分类器的目的。如果两个类是不平衡、不可分离的，且我们的目标是获得最大准确率，那么我们获得的分类器只会将数据点分到一个类中;不过这不是问题，而只是一个事实：针对这些变量，已经没有其他更好的选择了。

除了重采样外，我们还可以在数据集中添加一个或多个其他特征，使数据集更加丰富，这样我们可能获得更好的准确率结果。回到刚才的例子(两个类无法很好地分离开来)，我们附加一个新的特征帮助分离两个类，如下图所示：

$$寻找附加特征可以将原本不能分离的类分离开$$
与前一小节提到的重采样的方法相比，这种方法会使用更多来自现实的信息丰富数据，而不是改变数据的现实性。

重新解决问题更好

到目前为止，结论似乎令人失望：如果要求数据集代表真实数据而我们又无法获得任何额外特征，这时候如果我们以最佳准确率来评判分类器，那么我们得到的就是一个「naive behaviour」(判断结果总是同一个类)，这时候我们只好将之作为事实来接受。

但如果我们对这样的结果不满意呢?这就意味着，事实上我们的问题并没有得到很好的表示(否则我们应当可以接受模型结果)，因此我们应该重新解决我们的问题，从而获得期望结果。我们来看一个例子。

使用K-fold交叉验证

值得注意的是，使用过采样方法来解决不平衡问题时应适当地应用交叉验证。这是因为过采样会观察到罕见的样本，并根据分布函数应用自举法生成新的随机数据。有时由于数据生成没有代表性，会造成过拟合。

K-fold交叉验证就是把原始数据随机分成K个部分，在这K个部分中选择一个作为测试数据，剩余的K-1个作为训练数据。交叉验证的过程实际上是将实验重复做K次，每次实验都从K个部分中选择一个不同的部分作为测试数据，剩余的数据作为训练数据进行实验，最后把得到的K个实验结果平均。

这就是为什么在过度采样数据之前应该始终进行交叉验证，就像实现特征选择一样。只有重复采样数据可以将随机性引入到数据集中，以确保不会出现过拟合问题。

转化为一分类问题

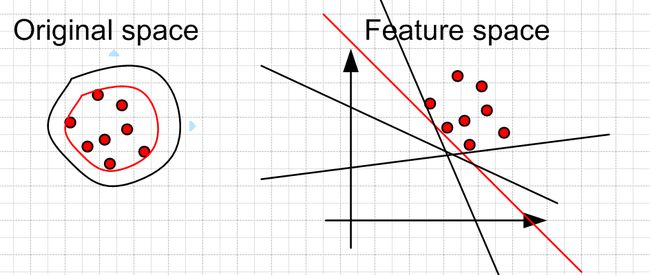
对于二分类问题，如果正负样本分布比例极不平衡，我们可以换一个完全不同的角度来看待问题：把它看做一分类（One Class Learning）或异常检测（Novelty Detection）问题。这类方法的重点不在于捕捉类间的差别，而是为其中一类进行建模，经典的工作包括One-class SVM等，如下图所示：

One Class SVM 是指你的训练数据只有一类正（或者负）样本的数据， 而没有另外的一类。在这时，你需要学习的实际上你训练数据的边界。而这时不能使用最大化软边缘了，因为你没有两类的数据。 所以呢，在这边文章中，“Estimating the support of a high-dimensional distribution”， Sch?lkopf 假设最好的边缘要远离特征空间中的原点。

左边是在原始空间中的边界，可以看到有很多的边界都符合要求，但是比较靠谱的是找一个比较紧的边界（红色的）。这个目标转换到特征空间就是找一个离原点比较远的边界，同样是红色的直线。当然这些约束条件都是人为加上去的，你可以按照你自己的需要采取相应的约束条件。比如让你data 的中心离原点最远。

对多数类进行聚类

Sergey Quora提出了一种优雅的方法。他建议不要依赖随机样本来覆盖训练样本的种类，而是将r个分组中的多数类进行聚类，其中r为r中的样本数。对于每个组，只保留质心（样本的中心）。然后该模型仅保留了少数类和样本质心来训练。

首先，我们可以对具有大量样本的多数类进行聚类操作。假设我们使用的方法是 K-Means聚类算法 。此时，我们可以选择K值为少数样本中的样本的个数，并将聚类后的中心点以及相应的聚类中心当做多数类样本的代表样例，类标与多数类类标一致。

聚类后的样本进行有监督学习

经过上述步骤的聚类操作，我们对多数类训练样本进行了筛选，接下来我们就可以将相等样本数的K个正负样本进行有监督训练。如下图所示：

设计模型算法

上面所有方法都集中在数据上，并将模型作为固定的组件。但事实上，如果模型适用于不平衡数据，则不需要对数据进行重新采样。著名的XGBoost已经是一个很好的起点，因为该模型内部对数据进行了很好的处理，它训练的数据并不是平衡的。

通过设计一个损失函数来惩罚少数类的错误分类，而不是多数类，可以设计出许多自然泛化为支持少数类的模型。例如，调整SVM以相同的比例惩罚未被充分代表的少数类的分类错误。

$$惩罚少数类的分类错误$$

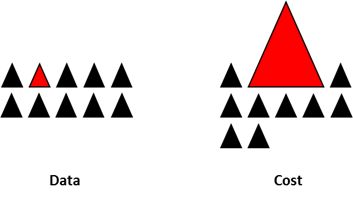
代价敏感——代价矩阵

上述的过采样和欠采样都是从样本的层面去克服样本的不平衡，从算法层面来说，克服样本不平衡。在现实任务中常会遇到这样的情况:不同类型的错误所造成的后果不同。

• 例如:在医疗诊断中，错误地把患者诊断为健康人与错误地把健康人诊断为患者，看起来都是犯了“一次错误”，但是后者的影响是增加了进一步检查的麻烦，前者的后果却可能是丧失了拯救生命的最佳时机;
• 再如，门禁系统错误地把可通行人员拦在门外，将使得用户体验不佳，但错误地把陌生人放进门内，则会造成严重的安全事故;
• 在信用卡盗用检查中，将正常使用误认为是盗用，可能会使用户体验不佳，但是将盗用误认为是正常使用，会使用户承受巨大的损失。

为了权衡不同类型错误所造成的不同损失，可为错误赋予“非均等代价”(unequal cost)。

代价矩阵与混淆矩阵非常相似。代价敏感方法的核心要素是代价矩阵, 如下图所示。 $\cos t_{ij}$​ 表示 将第 $i$​ 类样本预测为第 $j$​ 类样本的代价。一般来说, ${\mathrm{cost}}_{ii}=0$​; 若将第0类判定为第1类所造成的损失更大, 则 $\cos t_{01}>\cos t_{10}$​; 损失程度相差越大, $\cos t_{01}$​ 与 $\cos t_{10}$​ 的值差别越大。当 $\cos t_{01}$​ 与$\cos t_{10}$​ 相等时为代价不敏感的学习问题。

$$代价矩阵与混淆矩阵$$

1. 从学习模型出发，对某一具体学习方法的改造，使之能适应不平衡数据下的学习，研究者们针对不同的学习模型如感知机、支持向量机、决策树、神经网络等分别提出了其代价敏感的版本。以代价敏感的决策树为例，可以从三个方面对其进行改造以适应不平衡数据的学习，这三个方面分别是决策阈值的选择方面、分裂标准的选择方面、剪枝方面，这三个方面都可以将代价矩阵引入。
2. 从贝叶斯风险理论出发，把代价敏感学习看成是分类结果的一种后处理，按照传统方法学习到一个模型，以实现损失最小为目标对结果进行调整。此方法的优点在于它可以不依赖所用的具体分类器，但是缺点也很明显，它要求分类器输出值为概率。
3. 从预处理的角度出发，将代价用于权重调整，使得分类器满足代价敏感的特性

Metacost

目前常用的代价敏感学习,是根据两类错分代价的不同改变现有的分类算法，按照代价的比例变换训练集中类别的频率,缺点是改变了样本的分布,严重的影响了算法的性能,而且可能效果并不明显,因此, Domingos 提出了一种新的代价敏感学习方法—— Metacost.

Metacost 是一种后验调整法,其核心思想是代价最小化.它是在训练最终的分类器之前，进行单独的代价敏感学习,从而不会改变原有的算法．通过训练N个基本分类模型,得到训练样本的类别概率,通过代价最小化来修改训练集的类别标签,进而使用修改过类别标签的新的训练集建立分类模型.设某分类问题包含$J$​类,具体建模过程如下:

1. 在训练样本中用 Bagging 算法中的 Bootstrap 抽样方法多次取样, 生成 $N$​ 个训练子集;

2. 在每一个训练子集中用 DNN 算法建立模型, 一共训练 $N$ 个;

3. 使用 $N$ 个模型分别对训练集样本进行分类, 并通过集成得到训练集中每个样本 $x$ 属于第 $j$ 个类别的概率 $P(j\mid x)$ , 定义如下:

   $$P(j\mid x)=\frac{1}{N}\sum _j^{N}P\left(j\mid x,M_i\right)$$

   其中, $P\left(j\mid x,M_i\right)$ 是第 $i$ 个模型 $M_i$ 对样本 $x$ 属于类别 $j$ 的概率预测, $P(j\mid x)$ 表示 $N$ 个模型对样本 $x$ 属于类别 $j$​ 的概率的集成预测;

4. 计算每个训练样本在模型中的误分代价, 其定义如下:

   $$R(i\mid x)=\sum _{j}P(j\mid x)C(i,j),$$

   其中, $i$ 是样本的预测类别标签, $j$ 是样本的实际类别标签, $C(i,j)$ 是把第 $j$ 类的样本预测为第 $i$​ 类的损失;

   其中 $R(i\mid x)$ 表示将样本 $x$ 分为第 $i$ 类的期望代价,如果期望代价越小,则样本 $x$ 属于第 $i$ 类的概率就越大.计算每个样本属于各个类别的期望代价 $R(i\mid x)$, 并将训练集中的每一个实例重标记为代价最优的类.

5. 通过最小代价模型重新输出样本的类别标签, 并修改训练样本的类别标签, 得到新的经过类别标签修改的训练集, 其公式如下:
   $$x^{\prime }\text{ s class }=\arg \underset{i}{\min }\sum _{j}P(j\mid x)C(i,j).$$
   这里, 样本 $x$ 的类别标签等于 ${\sum }_{j}P(j\mid x)C(i,j)$ 取得最小值时所对应的类别标签 $i$;

6. 在新的训练集上训练分类模型,得到新的分类模型 $M$, 对测试集分类, 得到其分类结果.

其具体算法流程如图所示。

$$Metacost算法流程图$$

Focal loss

Focal loss是在标准交叉嫡损失基础上修改得到的，通过减少易分类样本的权重，使得模型在训练时更专注于难分类的样本。

Focal loss公式为：
$$FL(p_t)=-{\alpha }_t(1-p_t{)}^{\gamma }\log (p_t)$$

对比交叉熵函数，看看有什么区别
$$L_{ce}=-log(p_t)$$
这里详实的讲解了Focal loss：1.5 损失函数数学公式

focal loss相比交叉熵多了一个 $\alpha (1-p_t{)}^{\gamma }$ 。

from tensorflow import keras
import keras.backend as K

class FocalLoss(keras.losses.Loss):
    def __init__(self, gamma=2., alpha=4.,
                 reduction=keras.losses.Reduction.AUTO, name='focal_loss'):
        """Focal loss for multi-classification
        FL(p_t)=-alpha(1-p_t)^{gamma}ln(p_t)
        Notice: y_pred is probability after softmax
        gradient is d(Fl)/d(p_t) not d(Fl)/d(x) as described in paper
        d(Fl)/d(p_t) * [p_t(1-p_t)] = d(Fl)/d(x)
        Focal Loss for Dense Object Detection
        https://arxiv.org/abs/1708.02002

        Keyword Arguments:
            gamma {float} -- (default: {2.0})
            alpha {float} -- (default: {4.0})

        """
        super(FocalLoss, self).__init__(reduction=reduction,
                                        name=name)
        self.gamma = float(gamma)
        self.alpha = float(alpha)

    def call(self, y_true, y_pred):
        """
        Arguments:
            y_true {tensor} -- ground truth labels, shape of [batch_size, num_cls]
            y_pred {tensor} -- model's output, shape of [batch_size, num_cls]

        Returns:
            [tensor] -- loss.
        """
        epsilon = 1.e-9
        y_true = tf.convert_to_tensor(y_true, tf.float32)
        y_pred = tf.convert_to_tensor(y_pred, tf.float32)

        model_out = tf.add(y_pred,epsilon)
        cross_entropy  = tf.multiply(y_true, -tf.math.log(model_out))
        weight = tf.multiply(y_true, tf.pow(
            tf.subtract(1., model_out), self.gamma))
        FL = tf.multiply(self.alpha, tf.multiply(weight, cross_entropy ))
        reduced_fl = tf.reduce_max(FL, axis=1)
        return tf.reduce_mean(reduced_fl)

def binary_focal_loss(gamma=2.0, alpha=0.25):
    """
    Implementation of Focal Loss from the paper in multiclass classification
    Formula:
        loss = -alpha_t*((1-p_t)^gamma)*log(p_t)
        
        p_t = y_pred, if y_true = 1
        p_t = 1-y_pred, otherwise
        
        alpha_t = alpha, if y_true=1
        alpha_t = 1-alpha, otherwise
        
        cross_entropy = -log(p_t)
    Parameters:
        alpha -- the same as wighting factor in balanced cross entropy
        gamma -- focusing parameter for modulating factor (1-p)
    Default value:
        gamma -- 2.0 as mentioned in the paper
        alpha -- 0.25 as mentioned in the paper
    """
    def focal_loss(y_true, y_pred):
        # Define epsilon so that the backpropagation will not result in NaN
        # for 0 divisor case
        epsilon = K.epsilon()
        # Add the epsilon to prediction value
        #y_pred = y_pred + epsilon
        # Clip the prediciton value
        y_pred = K.clip(y_pred, epsilon, 1.0-epsilon)
        # Calculate p_t
        p_t = tf.where(K.equal(y_true, 1), y_pred, 1-y_pred)
        # Calculate alpha_t
        alpha_factor = K.ones_like(y_true)*alpha
        alpha_t = tf.where(K.equal(y_true, 1), alpha_factor, 1-alpha_factor)
        # Calculate cross entropy
        cross_entropy = -K.log(p_t)
        weight = alpha_t * K.pow((1-p_t), gamma)
        # Calculate focal loss
        loss = weight * cross_entropy
        # Sum the losses in mini_batch
        loss = K.sum(loss, axis=1)
        return loss
    
    return focal_loss   

评价指标

基础知识

混淆矩阵是机器学习中总结分类模型预测结果的情形分析表，以矩阵形式将数据集中的记录按照真实的类别与分类模型预测的类别判断两个标准进行汇总。

具体意义请看： 1,6 分类模型的评估方法

1）正确率（accuracy）

正确率是我们最常见的评价指标，，这个很容易理解，就是被分对的样本数除以所有的样本数，通常来说，正确率越高，分类器越好；

2）错误率（error rate)

错误率则与正确率相反，描述被分类器错分的比例，$errorrate=(FP+FN)/(TP+TN+FP+FN)$，对某一个实例来说，分对与分错是互斥事件，所以accuracy =1 - error rate；

3）召回率（recall）；灵敏度（sensitivity）也叫真阳性率 ；

$Recall=TP/(TP+FN)$，表示的是正确识别的正例个数在实际为正例的样本数中的占比，衡量了分类器对正例的识别能力；也叫"正例覆盖率"：表示正确预测的正例数在实际正例数中的比例。召回率是覆盖面的度量，该指标反映的是模型能够在多大程度上覆盖所关心的类别。

4）特异度（specificity)

$specificity=TN/（TN+FP）$，表示的是所有负例中被分对的比例，衡量了分类器对负例的识别能力；也叫"负例覆盖率"：正确预测的负例数在实际负例数中的比例。

5）精度（precision），精确率

精度是精确性的度量，表示正确预测的正例数在预测正例数中的比例，即$precision=TP/（TP+FP）$；也叫“正例命中率”。

这个指标在做市场营销的时候非常有用，例如对预测的目标人群做活动，实际响应的人数越 多，说明模型越能够刻画出关心的类别。

​ 6）F-Measure(F度量)

​ 计算公式为 :
$$F_{\beta }=\frac{\left({\beta }^2+1\right)PR}{{\beta }^{2}P+R}$$
​ 其中 $\beta$ 是参数， P是精确率(Precision), R是召回率(Recall)。$\beta =1$ 就是F1分数。

​ 7）F1分数(F1-Measure)
$$F1\text{-}score=\frac{2\times \text{Precision}\times \text{Recall}}{\text{Precision}+\text{Recall}}$$

统计学中的“第一类错误”和“第二类错误”，为我们把一些似是而非的问题讲透提供了一个工具。

第一类错误被称为“假阳性错误”，即错误的肯定，例如错抓好人、错误的诊断本来不存在的病。

第二类错误被称为“假阴性错误“，即错误的否定，即指错放坏人了、有病没查出来。

G-mean

在样本不均衡的情况下，由于少量样本占比较小, 如果仅考虑Error Rate或者 accuracy, 即使模型 全部把少量样本分错, 其整体的Error Rate和Accuracy还是比较 高的。因此, 对于样本不平衡的情况下，引入另外一个评价指标- $G$-mean。
$$G-Mean=\sqrt{\frac{TP}{TP+FN}\times \frac{TN}{TN+FP}}$$

MacroP, MicroP

Precision和Recall只是在一个简单的二分分类的情况下进行评价。当基于同一数据集多次训练/测试不同模型，或者基于多个数据集测试评价同一个模型，再或者执行多分类的任务时，会产生很多混淆矩阵。怎么评价？

macro-P宏查准率和macro-R宏查全率以及macro-F1:
$$\begin{array}{c}\mathrm{marcoP}=\frac{1}{n}\sum _1^n{P}_i\\ \mathrm{marco}R=\frac{1}{n}\sum _1^n{R}_i\\ \mathrm{marcoF}1=\frac{2\times \mathrm{macroP}\times \mathrm{macro}R}{\mathrm{macroP}+\text{ macro }R}\end{array}$$
micro-P微查准率和micro-P微查全率以及micro-F1:

与上面的宏不同，微查准查全，先将多个混淆矩阵的TP,FP,TN,FN对应位置求平均，然后按照P和R的公式求得micro-P和micro-R。最后根据micro-P和micro-R求得micro-F1
$$\begin{array}{c}\text{ microP }=\frac{\overline{TP}}{\overline{TP}\times \overline{FP}}\\ \text{ microR }=\frac{\overline{TP}}{\overline{TP}\times \overline{FN}}\\ \mathrm{mircoF}1=\frac{2\times \mathrm{microP}\times \mathrm{micro}R}{\mathrm{microP}+\mathrm{microR}}\end{array}$$
假设

y_true = [1, 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 4, 4]
y_pred = [1, 1, 1, 0, 0, 2, 2, 3, 3, 3, 4, 3, 4, 3]

Micro

首先计算总TP值，这个很好就算，就是数一数上面有多少个类别被正确分类，比如1这个类别有3个分正确，2有2个，3有2个，4有1个，那TP=3+2+2+1=8

其次计算总FP值，简单的说就是不属于某一个类别的元数被分到这个类别的数量，比如上面不属于4类的元素被分到4的有1个

如果还比较迷糊，我们在计算时候可以把4保留，其他全改成0，就可以更加清楚地看出4类别下面的FP数量了，其实这个原理就是 One-vs-All (OvA)，把4看成正类，其他看出负类

同理我们可以再计算FN的数量

	1类	2类	3类	4类	总数
TP	3	2	2	1	8
FP	0	0	3	1	4
FN	2	2	1	1	6

所以micro的 精确度P 为 TP/(TP+FP)=8/(8+4)=0.666 召回率R TP/(TP+FN)=8/(8+6)=0.571 所以F1-micro的值为：0.6153

可以用sklearn来核对,把average设置成micro

y_true = [1, 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 4, 4]
y_pred = [1, 1, 1, 0, 0, 2, 2, 3, 3, 3, 4, 3, 4, 3]
print(f1_score(y_true,y_pred,labels=[1,2,3,4],average='micro'))
#>>> 0.615384615385

Macro

先在各混淆矩阵先在各混淆矩阵上分别计算各类的查准率，查全率和F1，然后再计算平均值。

这样就得到“宏查准率”（macro-P）、“宏查全率”（macro-R）、“宏F1”（macro-F1）,最终求得就是“宏F1”

1类	2类	3类	4类	总数
TP	3	2	2	1	8
FP	0	0	3	1	4
FN	2	2	1	1	6

#注意这里，输出《宏F》
print(f1_score(y_true,y_pred,labels=[1,2,3,4],average='macro'))
#>>>0.604166666667

代码

 
from sklearn import metrics
 
y_test    = [1, 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 4, 4]
y_predict = [1, 1, 1, 0, 0, 2, 2, 3, 3, 3, 4, 3, 4, 3]
 
print('准确率:', metrics.accuracy_score(y_test, y_predict)) #预测准确率输出
 
print('宏平均精确率:',metrics.precision_score(y_test,y_predict,average='macro')) #预测宏平均精确率输出
print('微平均精确率:', metrics.precision_score(y_test, y_predict, average='micro')) #预测微平均精确率输出
print('加权平均精确率:', metrics.precision_score(y_test, y_predict, average='weighted')) #预测加权平均精确率输出
 
print('宏平均召回率:',metrics.recall_score(y_test,y_predict,average='macro'))#预测宏平均召回率输出
print('微平均召回率:',metrics.recall_score(y_test,y_predict,average='micro'))#预测微平均召回率输出
print('加权平均召回率:',metrics.recall_score(y_test,y_predict,average='micro'))#预测加权平均召回率输出
 
print('宏平均F1-score:',metrics.f1_score(y_test,y_predict,labels=[1,2,3,4],average='macro'))#预测宏平均f1-score输出
print('微平均F1-score:',metrics.f1_score(y_test,y_predict,labels=[1,2,3,4],average='micro'))#预测微平均f1-score输出
print('加权平均F1-score:',metrics.f1_score(y_test,y_predict,labels=[1,2,3,4],average='weighted'))#预测加权平均f1-score输出
 
print('混淆矩阵输出:\n',metrics.confusion_matrix(y_test,y_predict))#混淆矩阵输出
print('分类报告:\n', metrics.classification_report(y_test, y_predict))#分类报告输出
 
 
准确率: 0.5714285714285714
宏平均精确率: 0.58
微平均精确率: 0.5714285714285714
加权平均精确率: 0.7999999999999999
宏平均召回率: 0.4533333333333333
微平均召回率: 0.5714285714285714
加权平均召回率: 0.5714285714285714
宏平均F1-score: 0.6041666666666666
微平均F1-score: 0.6153846153846153
加权平均F1-score: 0.6369047619047619
混淆矩阵输出: 
[[0 0 0 0 0]
 [2 3 0 0 0]       #[1,0]为2，即1类预测为0的为2。[1,1]为3，则1类预测为1的为3。
 [0 0 2 2 0]
 [0 0 0 2 1]
 [0 0 0 1 1]]
分类报告:
              precision    recall  f1-score   support
 
          0       0.00      0.00      0.00         0
          1       1.00      0.60      0.75         5
          2       1.00      0.50      0.67         4
          3       0.40      0.67      0.50         3
          4       0.50      0.50      0.50         2
 
avg / total       0.80      0.57      0.64        14

ROC曲线和AUC

ROC曲线原理

ROC是受试者工作特征曲线(receiver operating characteristic curve ) 的简写，又称为感受性曲线(sensitivity curve)。得此名的原因在于曲线上各点反映着相同的感受性，它们都是对同一信号刺激的反应，只不过是在几种不同的判定标准下所得的结果而已.

在信号检测理论中，ROC曲线，是表示二元分类器系统在识别阈值变化时性能的图形图。

ROC曲线的横轴是FPR（$\boxed{假阳性率}$、误诊率）、纵轴是TPR（$\boxed{真阳性率}$​、灵敏度）。

• 真正率(TPR) = 灵敏度(Sensitivity) = TP/(TP+FN)
• 假正率(FPR) = 1-特异度(Specificity) = FP/(FP+TN)

AUC原理

AUC（Area Under Curve）被定义为ROC曲线下的面积，取值范围一般在0.5和1之间。使用AUC值作为评价标准是因为很多时候ROC曲线并不能清晰的说明哪个分类器的效果更好，而作为一个数值，对应AUC更大的分类器效果更好。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-cn9iwUDx-1629395097815)(https://i04piccdn.sogoucdn.com/6d35ad97577c17b2#pic_center)]

$$AUC$$

• AUC = 1，是完美分类器，采用这个预测模型时，存在至少一个阈值能得出完美预测。绝大多数预测的场合，不存在完美分类器。
• 0.5 < AUC < 1，优于随机猜测。这个分类器（模型）妥善设定阈值的话，能有预测价值。
• AUC = 0.5，跟随机猜测一样（例：丢铜板），模型没有预测价值。
• AUC < 0.5，比随机猜测还差；但只要总是反预测而行，就优于随机猜测。

可以看出，AUC 在最佳情况下将趋近于 1.0，而在最坏情况下降趋向于 0.5。同样，一个好的 AUC 分数意味着我们评估的模型并没有为获得某个类（通常是少数类）的高召回率而牺牲很多精度。

PR-AUC曲线

• 纵坐标查准率，即精确率(Precision)·
• 横坐标查全率，即召回率(Recall)

为什么使用ROC曲线

既然已经这么多评价标准，为什么还要使用ROC和AUC呢？因为ROC曲线有个很好的特性：当测试集中的正负样本的分布变化的时候，ROC曲线能够保持不变。在实际的数据集中经常会出现类不平衡（class imbalance）现象，即负样本比正样本多很多（或者相反），而且测试数据中的正负样本的分布也可能随着时间变化。下图是ROC曲线和Precision-Recall曲线[^5]的对比：

在上图中，(a)和©为ROC曲线，(b)和(d)为Precision-Recall曲线。(a)和(b)展示的是分类其在原始测试集（正负样本分布平衡）的结果，©和(d)是将测试集中负样本的数量增加到原来的10倍后，分类器的结果。可以明显的看出，ROC曲线基本保持原貌，而Precision-Recall曲线则变化较大。

ROC-Curve和PR-Curve的应用场景

• ROC曲线由于兼顾正例与负例，所以适用于评估分类器的整体性能，相比而言PR曲线完全聚焦于正例。
• 如果有多份数据且存在不同的类别分布，比如信用卡欺诈问题中每个月正例和负例的比例可能都不相同，这时候如果只想单纯地比较分类器的性能且剔除奚别分布改变的影响，则ROC曲线比较适合,因为类别分希改变可能使得PR曲线发生变化时好时坏，这种时候难以进行模型比较;反之，如果想测试不同类别分布下对分类器的性能的影响，则PR曲线比较适合。
• 如果想要评估在相同的类别分布下正例的预测情况，则宜选PR曲线。
• 类别不平衡问题中，ROC曲线通常会给出一个乐观的效果估计，所以大部分时候还是PR曲线更好。
• 最后可以根据具体的应用，在曲线上找到最优的点，得到相对应的precision,recall, f1 score等指标，去调整模型的阂值，从而得到一个符合真体应用的模型。

应用实战

此次信用卡欺诈是采用科赛数据科学社区一个项目的数据集来分析的，具体的数据集可以在这里下载 传送门

数据集解读

• 在284807交易记录中，有492条欺诈记录，属于样本极不平衡
• 数据集仅包含数值数据是因为做了PCA变换，特征V1到V28是通过PCA变换得到的主成分
• 其中Time以及Amount数据是没有做PCA变换的
  其中数据字段解读如下表所示：

数据探索

这个数据集一共有28万多的数据，是一个非常大的数据集，在Excel中打开会卡顿，所以最好的是用pandas来操作。

# 导入第三方包
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn import model_selection
from sklearn import tree
from sklearn import metrics
from imblearn.over_sampling import SMOTE
#查看数据
data = pd.read_csv(r'\信用卡欺诈\creditcard.csv')
data.head()

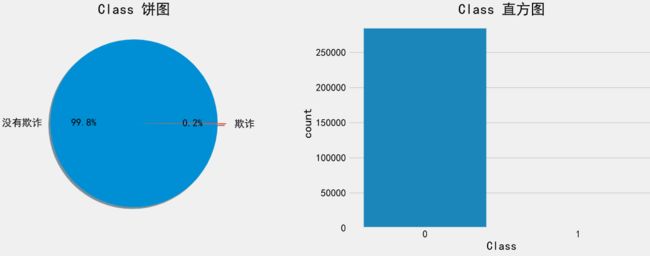
print(data.groupby('Class').size())
sns.countplot(x="Class", data=data)

Class
0    284315
1       492
dtype: int64

可以看到正真为欺诈类的数据非常的少，数据集是极度的不均匀，所以需要对数据集进行一定的处理

数据规范化

由于数据集并没有什么缺失数据之类的，而且28个主成分是已经由PCA进行转换的，所以28个主成分不需要做处理，只有Time还有Amount这两列需要处理，Time这一列对分类没什么作用，这里做删除处理，Amount列做标准化处理

from sklearn.preprocessing import StandardScaler  # 标准化工具

ss = StandardScaler()
data.Amount = ss.fit_transform(data['Amount'].values.reshape(-1,1))
data1 = data.drop(['Time'],axis=1)

得到的数据集就是标准化后的数据集

数据集划分

这里将数据集按按照训练集：测试集 = 8：2来划分数据集

data1=data1.sample(frac=1)#打乱数据
X = data1.iloc[:,0:29].values
y = data1.iloc[:,29].values
X_train,X_test,y_train,y_test=model_selection.train_test_split(X,y,test_size=0.2,stratify=y,random_state=1)

print(sum(y_train==1))
print(sum(y_train==0))

#out
394
227451

这里先不处理不平衡数据看看模型效果

模型创建

这里的数据集数量太大，本人尝试用SVC来分类，结果发现所需时间实在是太久了，SVM的确不适合大数据集，这里我们使用逻辑回归来进行分析建模,首先最优参数C

params = {
     'C':[1,2,3,4,5,6,7,8,9,10]}
lr = linear_model.LogisticRegression()
lr_clf = GridSearchCV(lr,params,cv=5,n_jobs=-1)
lr_clf.fit(X_train,y_train)
print(lr_clf.best_params_ )

#out
{
     'C': 1}

得到最优参数为1，将参数C=1重新训练测试

lr = linear_model.LogisticRegression(C=1)
lr_model = lr.fit(X_train,y_train)
y_predict = lr_model.predict(X_test)
print('准确率：',metrics.accuracy_score(y_test, y_predict))

#out
准确率： 0.9991748885221726

哇，准确率为 99.91％。太好了吧？也许模型整体的准确率仅反映了该模型在整个集合中的表现，而并没有反映我们在检测欺诈性记录方面的表现。要查看我们的实际效果如何，需要打印混淆矩阵和准确性报告。

print(metrics.classification_report(y_test, y_predict))
fig,ax = plt.subplots(1,2,figsize=(15,5))#一行两列，
cm = metrics.confusion_matrix(y_test,  y_predict)
cmd = metrics.ConfusionMatrixDisplay(cm, display_labels=['No Fraud','Fraud'])
cmd.plot(ax=ax[0])

cm_normalized = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
cmd1 = metrics.ConfusionMatrixDisplay(cm_normalized, display_labels=['No Fraud','Fraud'])
cmd1.plot(ax=ax[1])
ax[0].set_title('confusion matrix')
ax[1].set_title('Normalized confusion matrix')
plt.show()
#out
              precision    recall  f1-score   support

           0       1.00      1.00      1.00     56864
           1       0.87      0.61      0.72        98

    accuracy                           1.00     56962
   macro avg       0.93      0.81      0.86     56962
weighted avg       1.00      1.00      1.00     56962

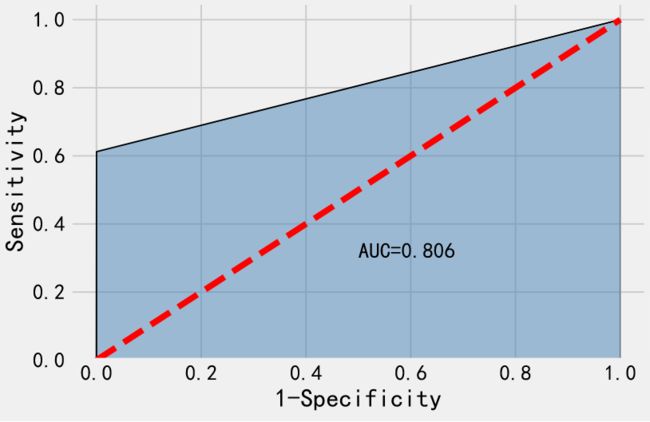
从上面我们可以看到，尽管总体准确率为99.91％，但我们在测试集中错误的分类了 39% 的欺诈案例！这就是不合格预测了，再来看看AUC得分：

fpr, tpr, thresholds = metrics.roc_curve(y_test, y_predict)#计算假正率和真正率
roc_auc = metrics.auc(fpr, tpr)
# 绘制面积图
plt.stackplot(fpr, tpr, color='steelblue', alpha = 0.5, edgecolor = 'black')
# 添加边际线
plt.plot(fpr, tpr, color='black', lw = 1)
# 添加对角线
plt.plot([0,1],[0,1], color = 'red', linestyle = '--')
# 添加文本信息
plt.text(0.5,0.3,'AUC=%0.3f' % roc_auc)
# 添加x轴与y轴标签
plt.xlabel('1-Specificity')
plt.ylabel('Sensitivity')
# 显示图形
plt.show()

进行交叉验证看看是不是偶然事件：

model = linear_model.LogisticRegression(random_state = 1,C=1)
y_predict  = model_selection.cross_val_predict(model,X ,y ,cv=10)
print(metrics.classification_report(y, y_predict))

#out
              precision    recall  f1-score   support

           0       1.00      1.00      1.00    284315
           1       0.87      0.62      0.73       492

    accuracy                           1.00    284807
   macro avg       0.93      0.81      0.86    284807
weighted avg       1.00      1.00      1.00    284807

合成少数类过采样技术

数据科学界中一种实现此目标的流行技术称为 SMOTE(Synthetic Minority Oversampling Technique)，由 Nitesh Chawla 等人在他们 2002 年的论文中提出。SMOTE 的原理是从少样本类别中选择样本，找到它们在少样本类别中的最近邻居，并在它们之间有效地插值新点。虽然 SMOTE 不能插入少样本类别之外的数据记录，但在我们的情景中却可能包含有用的信息 —— 它可以将疑似欺诈或者标注错误的记录引入数据集中。

smote = SMOTE(random_state=1)     #  合成少数类过采样技术
X_train_smote,y_train_smote = smote.fit_sample(X_train,y_train)
print(sum(y_train_smote==1))
print(sum(y_train_smote==0))

#out
227451
227451

这里我们使用逻辑回归来进行分析建模,首先最优参数C

params = {
     'C':[1,2,3,4,5,6,7,8,9,10]}
lr = LogisticRegression()
lr_clf = GridSearchCV(lr,params,cv=5,n_jobs=-1)
lr_clf.fit(X_train_smote,y_train_smote)
print(lr_clf.best_params_ )

#out
{
     'C': 6}

得到最优参数为6，将参数C=6重新训练测试

lr = linear_model.LogisticRegression(C=6)
model = lr.fit(X_train_smote, y_train_smote)
y_predict = model.predict(X_test)

打印混淆矩阵和准确性报告。

print(metrics.classification_report(y_test, y_predict))
cm = metrics.confusion_matrix(y_test,  y_predict)
cmd = metrics.ConfusionMatrixDisplay(cm, display_labels=['No Fraud','Fraud'])
cmd.plot()
#out
              precision    recall  f1-score   support

           0       1.00      0.97      0.99     56864
           1       0.05      0.94      0.10        98

    accuracy                           0.97     56962
   macro avg       0.53      0.96      0.54     56962
weighted avg       1.00      0.97      0.98     56962

虽然欺诈和不欺诈的数据正确率都提高了。然而，这最终导致出现一个毛病：几乎所有欺诈行为都被检测到，但是这样就会有很多假阴性…

再来看看AUC得分：

fpr, tpr, thresholds = metrics.roc_curve(y_test, y_predict)#计算假正率和真正率
roc_auc = metrics.auc(fpr, tpr)
# 绘制面积图
plt.stackplot(fpr, tpr, color='steelblue', alpha = 0.5, edgecolor = 'black')
# 添加边际线
plt.plot(fpr, tpr, color='black', lw = 1)
# 添加对角线
plt.plot([0,1],[0,1], color = 'red', linestyle = '--')
# 添加文本信息
plt.text(0.5,0.3,'AUC=%0.3f' % roc_auc)
# 添加x轴与y轴标签
plt.xlabel('1-Specificity')
plt.ylabel('Sensitivity')
# 显示图形
plt.show()

最终得到的AUC值为0.955，远大于0.8，此时就可以认为模型比较合理了。

准确率高是预料之中的，即使使用样本分布均匀的数据集来进行训练，由于测试集的负样本数据太少，而测试的样本不能随便由SMOTE生成，这样子会使得模型的拟合和评估都在生成的数据上进行，模型没有可信度，只有在真实的数据集进行预测才有可信力.

误差加权

解决方案是告诉逻辑回归存在类别不平衡，并对误差加权，权重与类别不平衡成比例.

lr = LogisticRegression(class_weight='balanced')
 
# Fit..
lr.fit(X_train, y_train)
 
# Predict..
y_pred = lr.predict(X_test)
 
# Evaluate the model
print(classification_report(y_test, y_pred))
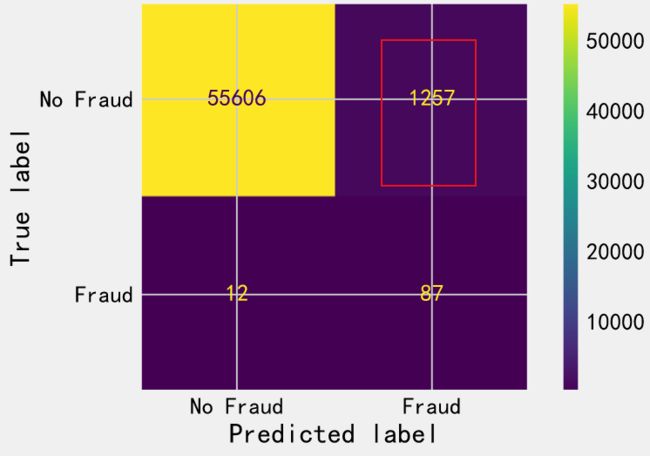
# 构建混淆矩阵
cm = metrics.confusion_matrix(y_test,  y_pred)
cmd = metrics.ConfusionMatrixDisplay(cm, display_labels=['No Fraud','Fraud'])
cmd.plot()

然而，这最终导致出现一个毛病：几乎所有欺诈行为都被检测到，但是这样就会有很多假阴性…

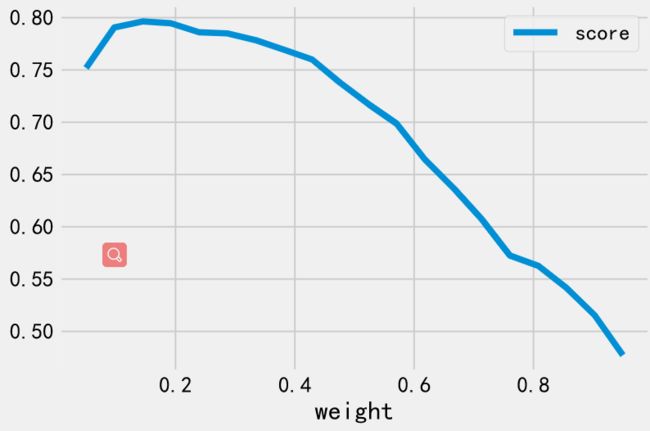
为了减少假阴性，我们使用F1作为损失函数来衡量模型好坏，下面就来看看调整权重 对F1的影响：

from sklearn.model_selection import GridSearchCV
 
weights = np.linspace(0.05, 0.95, 20)
 
gsc = GridSearchCV(
    estimator=LogisticRegression(),
    param_grid={
     
        'class_weight': [{
     0: x, 1: 1.0-x} for x in weights]
    },
    scoring='f1',
    cv=3
)
grid_result = gsc.fit(X, y)
 
print("Best parameters : %s" % grid_result.best_params_)
 
# Plot the weights vs f1 score
dataz = pd.DataFrame({
      'score': grid_result.cv_results_['mean_test_score'],
                       'weight': weights })
dataz.plot(x='weight')

通过优化参数我们又训练了一个LR模型，这个模型的性能就好多了.

lr = LogisticRegression(**grid_result.best_params_)
# Fit..
lr.fit(X_train, y_train)
# Predict..
y_pred = lr.predict(X_test)
# Evaluate the model
print(classification_report(y_test, y_pred))
# 构建混淆矩阵
cm = metrics.confusion_matrix(y_test,  y_pred)
cmd = metrics.ConfusionMatrixDisplay(cm, display_labels=['No Fraud','Fraud'])
cmd.plot()

#out
              precision    recall  f1-score   support

           0       1.00      1.00      1.00     56864
           1       0.78      0.78      0.78        98

    accuracy                           1.00     56962
   macro avg       0.89      0.89      0.89     56962
weighted avg       1.00      1.00      1.00     56962

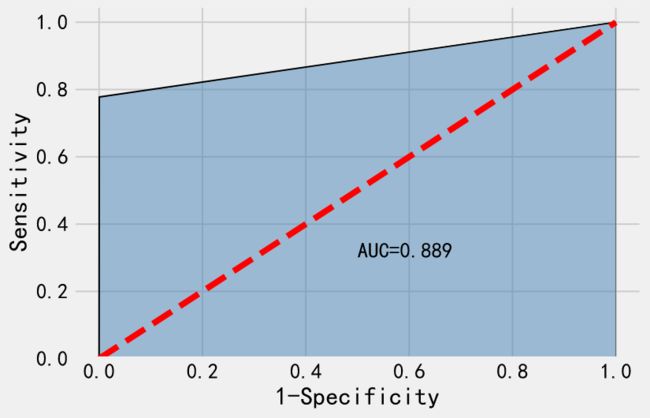
fpr, tpr, thresholds = metrics.roc_curve(y_test, y_pred)#计算假正率和真正率
roc_auc = metrics.auc(fpr, tpr)
# 绘制面积图
plt.stackplot(fpr, tpr, color='steelblue', alpha = 0.5, edgecolor = 'black')
# 添加边际线
plt.plot(fpr, tpr, color='black', lw = 1)
# 添加对角线
plt.plot([0,1],[0,1], color = 'red', linestyle = '--')
# 添加文本信息
plt.text(0.5,0.3,'AUC=%0.3f' % roc_auc)
# 添加x轴与y轴标签
plt.xlabel('1-Specificity')
plt.ylabel('Sensitivity')
# 显示图形
plt.show()

最终得到的AUC值为0.889，远大于0.8，此时就可以认为模型比较合理了。

Bagging

bc = BaggingClassifier(base_estimator=DecisionTreeClassifier(),
                       random_state=0)
bc.fit(X_train, y_train)

y_pred = bc.predict(X_test)
# Evaluate the model
print(classification_report(y_test, y_pred))
# 构建混淆矩阵
cm = metrics.confusion_matrix(y_test,  y_pred)
cmd = metrics.ConfusionMatrixDisplay(cm, display_labels=['No Fraud','Fraud'])
cmd.plot()

#out
              precision    recall  f1-score   support

           0       1.00      1.00      1.00     56864
           1       0.94      0.77      0.84        98

    accuracy                           1.00     56962
   macro avg       0.97      0.88      0.92     56962
weighted avg       1.00      1.00      1.00     56962

这个Bagging对于F1分数的提升蛮大的，哈哈哈。

参考

https://www.baidu.com/link?url=zDAiD84L7GSGqWHotPBLr-dTwXZvnuiY8jKwvBSHbwNGF2o3CBNGuYnKG13hRK27eypGiyNzQAc95J_fp2wDD_&wd=&eqid=e142fe27000081bf00000006606316a9

https://blog.csdn.net/wangzi11111111/article/details/88629619

https://zhuanlan.zhihu.com/p/245504387

https://microstrong.blog.csdn.net/article/details/80287033?utm_medium=distribute.pc_relevant.none-task-blog-2_defaultBlogCommendFromMachineLearnPai2_{default-4.control&dist_request_id=&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2}default_{BlogCommendFromMachineLearnPai2}default-4.control

SMOTE算法

不平衡数据处理

Imblearn包官网

Imblearn GitHub

稀疏矩阵CRS存储

常见稀疏矩阵存储方法总结

稀疏矩阵存储Scipy官方文档

Python sklearn 实现过采样和欠采样