一文弄懂交叉熵损失

引言

今天来好好地捋一捋交叉熵损失(Cross Entropy Loss)。
从信息熵入手，再到极大似然估计，然后引入KL散度，最后来看KL散度与交叉熵的关系。
虽然文章有点长，但相信看完本文，你一定会对交叉熵损失有更高一层的领悟。

信息熵

信息的价值在于消除事件的不确定性，那事件的不确定性要怎么度量呢？答案就是信息熵(information entropy)。

比如你告诉别人你中了500万彩票，别人会大吃一惊，因为他被消除了大量的不确定性。但如果你告诉别人你没中彩票，别人基本熵没有反应，因为他估计你这小子十有八九不会中彩票。相当于你几乎没有消除他对你没有中彩票这件事的不确定性。或者说你传达的信息量太少。我们知道概率只能在0到1之间，也就是说，最好在概率为1的时候，信息量为0，且概率越小，信息量越大。后来人们发现，对数函数很符合这样的规律，某个事件的信息量与概率的关系是$i=\log (\frac{1}{p})$，这里的对数是以2为底的，$p$是事件发生的概率。

上面最后这个式子是怎么来的呢？以抛硬币游戏为例，如果有一枚理想的硬币，其出现正面和反面的概率相等，假设我们相隔很远，只能通过电位信号(0或1)进行交流，如何把这个硬币的结果告诉我呢。显然，此时只需要发送一个信号就可以，用1表示正面，用0表示反面。信息的价值在于消除事件的不确定性，传递一枚硬币结果的信息，帮我们消除了它是哪一个面的不确定性。

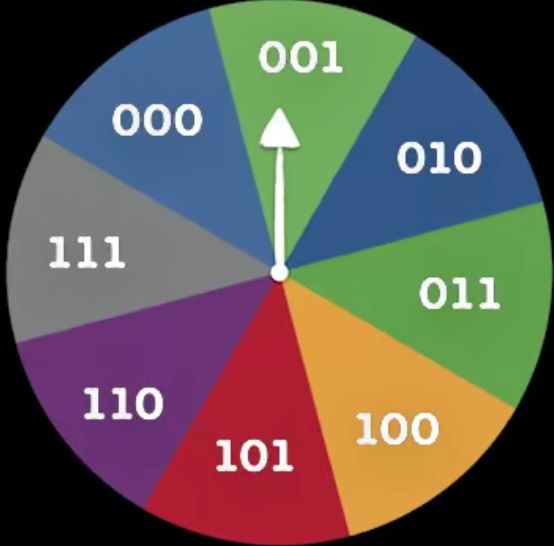
我们再来看一个转盘游戏，这个转盘被均等地分为8个区域，如果我们要把转盘的结果发送出去，那么需要多少个信号呢？答案是3个信号。

在这两个例子中，我们发现一件事情，把一个游戏系统中所有可能出现的等概率事件数量取以2为底的对数，就是我们要传递事件结果所需要的信号数量。比如在抛硬币游戏中是${\log }_2(2)=1$，在转盘游戏中是${\log }_2(8)=3$​​。这个数量就是信息量。

即$\text{信息量}=\log (N)$，这里的$N$是等可能事件数量。

可以把这种度量不确定性的信息量称为信息熵，但严格来说这并不是香农所说的信息熵，这只是信息熵的一个特例，即所有的事件是等可能的。我们遇到的更多情况是事件发生的可能性不一样的系统。 比如现实生活中就无法制作出来正反面概率都是50%的硬币。

实际上，我们总是可以把一个事件的概率值转换为一个等可能事件系统中发生某个事件的概率。举例来说，我们总是可以把一个概率值转换为“在N个球中随机摸一个球”这个等可能事件系统中摸出某个球的概率。

假设中彩票大奖的概率很低，只有两千万分之一，我们可以把这个概率值转换为在两千万个球中摸出中奖球的概率。在这个摸球系统中，就有两千万个等可能事件。所以只需要用1除以概率值就可以想象出等可能事件系统中事件等数量，即$N=\frac{1}{p}$​。

假设我们有一个动了手脚的不均匀硬币，它正面朝上的概率是0.8，反面朝上的概率是0.2。

如上图，反面朝上0.2的概率可以想象有5个球的摸球系统中摸出某个球的概率。

而正面朝上0.8的概率可以想象成在有1.25个球的系统中摸出某个球的概率。我们通过想象把一个非等概率事件的系统拆成了两个等概率事件的系统。

而面对等概率事件系统，我们就可以很容易地计算它们的信息量。再把这两个想象出来的摸球系统的信息量加起来，就是这个不均匀硬币的信息量：$\log 5+\log 1.25$，由于这两个我们想象出来的等概率系统本身出现的概率也不一样，因此我们需要分别乘上它们出现的概率，得$0.2\cdot \log 5+0.8\cdot \log 1.25$。

如果我们用符号去抽象这些具体的值，就是
$$p_1\cdot \log \frac{1}{p_1}+p_2\cdot \log \frac{1}{p_2}\text{\hspace{1em}(1)}$$
对于有更多事件的一般情况，我们可以这么表示：
$$\sum _i{p}_i\log \frac{1}{p_i}\text{\hspace{1em}(2)}$$
我们整理下这个式子
$$\begin{array}{rl}\sum _i{p}_i\log \frac{1}{p_i}& =\sum _i(p_i\cdot (\log 1-\log p_i))\\ & =\sum _i-p_i\log p_i\\ & =-\sum _i{p}_i\log p_i\end{array}\text{\hspace{1em}(3)}$$

就得到了香农所提出的信息熵公式 $-{\sum }_i{p}_i\log p_i$

我们可以看出，信息熵实际熵就是我们给每个概率值想象出来的某球系统的信息量的平均值，或者说是信息量的期望。

如果我们要比较两个概率模型的距离，最简单的办法就是把它们的信息熵都算出来，直接比较两个结果就好了。但是问题是，在机器学习中，我们往往不知道训练样本的概率模型。此时呢，我们就需要用到相对熵，也称为KL散度(KL Divergence)。

但是在这之前，为了知识的完整性，我们需要了解极大似然估计的概念。

极大似然估计

极大似然估计里面有三个概念，极大、似然和估计。通俗来说，就是用已知的样本结果信息，去反推最有可能导致这些样本结果出现的模型参数值。

反推说的是一种推理、估计，我们无法保证完全能从已知样本去推出产生这些样本的概率分布，只能说是一种估计。似然值说的是，真实样本已经看到，假设有很多(概率)模型，每个模型产生这些真实样本的可能性就叫似然值。极大似然估计就是选择似然值最高的模型来估计真实(概率)模型。

还是以抛硬币为例，我们记硬币的正面为H(Head)，反面为T(Tail)。

假设我们不知道这个硬币产生正反面的概率，但是我们可以做10次实验，假设产生这样一组结果：HHHHHHHTTT。即前7次是正面，后3次是反面。

假设有三个产生这组结果的模型(概率分布)，

• 模型A产生正面的概率$p=0.1$，产生反面的概率就是$1-p=0.9$​
• 模型B产生正面的概率$p=0.7$，产生反面的概率是$1-p=0.3$
• 模型$C$产生正面的概率$p=0.8$，产生反面的概率是$1-p=0.2$

计算某个概率模型产生这组结果的可能性是可以计算出来的，公式为：
$$P(C_1,C_2,\cdots ,C_{10}|\theta )=\prod _{i=1}^{10}P(C_i|\theta )\text{\hspace{1em}(4)}$$
其中$C_i\in \{0,1\}$是第$i$次抛硬币的结果，整个式子说的是由参数$\theta$确定的模型同时发生$C_1,C_2,\cdots ,C_{10}$的概率。

同时发生就是连乘。

这样的可能性就叫似然值。

因此我们只需要计算每个模型的似然值，然后选择似然值最大的模型来估计真实模型。

模型$A$的似然值：$0.1^{7}0.9^3\approx 7.29e-08$

模型$B$的似然值：$0.7^{7}0.3^3\approx 0.00222$

模型$C$的似然值：$0.1^{7}0.9^3\approx 0.00168$

挑出似然值最大的模型就叫最大似然估计法。

极大似然法

我们从极大似然估计的角度来看一下损失函数的选择。

以上图为例，把一些图片，输入到神经网络，神经网络会输出这张图片是猫的可能性。假设这些图片是训练数据，我们已经这些图片是否是猫。

在抛硬币中，我们通过$\theta$来表示参数，在神经网络这里可以具体地用$W,b$来表示。

即可以写成：
$$P(x_1,x_2,x_3,\cdots ,x_n|W,b)\text{\hspace{1em}(5)}$$
$n$这些图片的个数；$x_i\in \{0,1\}$代表输入的这张图片是否为猫，$1$代表是猫。

这样我们也可以把上式改成连乘的形式：
$$P(x_1,x_2,x_3,\cdots ,x_n|W,b)=\prod _{i=1}^{n}P(x_i|W,b)\text{\hspace{1em}(6)}$$
我们就可以得到基于这些图片的模型的似然值，我们要找到使得这个似然值最大的$W,b$。

但是$W,b$​是一个确定的值，而我们知道神经网络可以看成是由$W,b$这组参数确定的一个函数，该函数的输出结果$y_i$表示输入图片$x_i$是猫的可能性有多大，即$y_i=N{N}_{W,b}(x_i)$​​。这里我们就可以用可能性$y_i$来替代上面的参数$W,b$：
$$P(x_1,x_2,x_3,\cdots ,x_n|W,b)=\prod _{i=1}^{n}P(x_i|y_i)\text{\hspace{1em}(7)}$$
这样输入不同猫的图片$x_i$，我们可以得到不同的概率值$y_i$。

这个式子我们要如何展开呢，我们这个连乘时的写法与$x_i$的取值有关，当$x_i=1$时，输出的应该是判断为猫的概率，取$y_i$；当$x_i=0$时，输出的应该是判断不是猫的概率，取$1-y_i$。

好在还是有解法的，这个式子可以通过伯努利分布展开的，因为$x_i\in \{0,1\}$两种情况，同时$y_i$又是一个概率。

和抛硬币的例子类似，当$x=1$时，我们用硬币是正面的概率$p$去乘；当$x=0$是，我们用硬币是反面的概率$1-p$去乘。

我们就可以通过伯努利分布的这个式子来展开式$(7)$，得：
$$P(x_1,x_2,x_3,\cdots ,x_n|W,b)=\prod _{i=1}^n{y}_i^{x_i}(1-y_i{)}^{1-x_i}\text{\hspace{1em}(8)}$$
我们通过在等式右边取对数，把连乘变成连加，因为取对数不改变单调性的。
$$\begin{array}{rl}\log \left(\prod _{i=1}^n{y}_i^{x_i}(1-y_i{)}^{1-x_i}\right)& =\sum _{i=1}^n\log \left(y_i^{x_i}(1-y_i{)}^{1-x_i}\right)\\ & =\sum _{i=1}^n\left(x_i\cdot \log y_i+(1-x_i)\cdot \log (1-y_i)\right)\end{array}\text{\hspace{1em}(9)}$$

我们要求极大似然值，是取的最大值，而损失函数是取最小值，我们把等式两边乘以一个负号，变成了求最小值。
$$\min -\sum _{i=1}^n\left(x_i\cdot \log y_i+(1-x_i)\cdot \log (1-y_i)\right)\text{\hspace{1em}(10)}$$
虽然这个式子看起来很像交叉熵，但实际上还是有很大不同的，主要的区别是它们的量纲不同。

这里面的对数是我们故意加上去的，并且负号也是为了凑成求最小值。

下面我们就来了解相对熵。

KL散度

KL散度，也被称为相对熵，是用来衡量两个分布的距离，设$P$和$Q$是两个概率分布，则$P$对$Q$的相对熵为：
$$D_{KL}(P||Q)=\sum _{i}P(i)\log \frac{P(i)}{Q(i)}\text{\hspace{1em}(11)}$$
这里$i$代表分布中的所有类别。

性质

1. 不具备对称性，即$D(P||Q)\ne D(Q||P)$
2. 非负性，即$D(P||Q)\ge 0$

举个例子，还是以抛硬币为例，假设我们有一个公平的硬币，即正反概率都是50%；我们还有一个有偏差的硬币，其正面概率为$p$，反面概率为$q$。

我们要如何判断这两个分布的相似性呢？

可能不好回答，但是我们知道，如果$p=0.55$，它肯定比$p=0.95$要更相似。

我们可以从抛硬币的结果来看，

​ 假设公平硬币的抛掷结果为：HHTHHTTHTHTH

假设$p=0.55$硬币的抛掷结果为：HHTHHTTHHHTH

假设$p=0.95$硬币的抛掷结果为：HHHHHHTHHHHH

我们可以简单的计算不相等的结果个数，但是更严谨的做法是计算产生某个结果的似然值。

如果似然值很接近，那么说明这两个概率分布很接近。

基于(公平硬币抛出的)观察结果，我们就可以计算公平硬币的似然值和其他硬币的似然值的比值：
$$\frac{P(\text{观察结果}|\text{公平硬币})}{P(\text{观察结果}|\text{偏差硬币})}$$
我们再举一个例子，假设有一枚硬币，其正面概率为$p_1$，反面概率为$p_2$；

假设我们抛掷这枚硬币12次，产生的结果为：HHTHHTHHHTHT

我们可以很容易计算出这枚硬币产生这个结果的概率： $p_1\cdot p_1\cdot p_2\cdot p_1\cdot p_1\cdot p_2\cdot p_1\cdot p_1\cdot p_1\cdot p_2\cdot p_1\cdot p_2$

我们再拿一枚硬币，它产生正面的概率为$q_1$，反面概率为$q_2$

那么这枚新的硬币产生这个结果的概率为： $q_1\cdot q_1\cdot q_2\cdot q_1\cdot q_1\cdot q_2\cdot q_1\cdot q_1\cdot q_1\cdot q_2\cdot q_1\cdot q_2$

即基于观察结果，有

$P(\text{观察结果}|\text{硬币1})=p_1^{N_H}{p}_2^{N_T}$

$P(\text{观察结果}|\text{硬币2})=q_1^{N_H}{q}_2^{N_T}$

其中$N_H$​表示观察结果中为正面的次数，$N_T$​为反面的次数。我们计算它们的比值：
$$\frac{P(\text{观察结果}|\text{真实硬币})}{P(\text{观察结果}|\text{硬币2})}=\frac{p_1^{N_H}{p}_2^{N_T}}{q_1^{N_H}{q}_2^{N_T}}\text{\hspace{1em}(12)}$$
这样就能计算出来这两个硬币的相似性。

其实KL散度衡量的是类似的东西。怎么说？

我们把上式右边取对数，并除以实验总数$N=N_H+N_T$：
$$\begin{array}{rl}\frac{1}{N}\log \left(\frac{p_1^{N_H}{p}_2^{N_T}}{q_1^{N_H}{q}_2^{N_T}}\right)& =\frac{1}{N}\log p_1^{N_H}+\frac{1}{N}\log p_2^{N_T}-\frac{1}{N}\log q_1^{N_H}-\frac{1}{N}\log q_2^{N_T}\\ & =p_1\log p_1+p_2\log p_2-p_1\log q_1-p_2\log q_2\\ & =p_1\log \frac{p_1}{q_1}+p_2\log \frac{p_2}{q_2}\end{array}$$

其中$\frac{N_H}{N}=p_1\frac{N_T}{N}=p_2$。这里$p$是一个概率分布，$q$是另一个概率分布，该式子和KL散度的式子一模一样。

即我们通过计算真实分布的似然值除以第二个分布的似然值，再取归一化的对数，就得到了KL散度的表达式。

我们可以看到，KL散度是一种衡量两个概率分布距离的方式，通过观察第二个概率分布产生第一个概率分布样本的可能性。

KL散度非常适用于深度学习的场景，因为深度学习模型基本上是关于为已知样本的真实分布建模。

实际上，交叉熵损失(cross entroy loss)就等于KL损失，最小化交叉熵就是最小化两个分布的距离。

我们先来看下交叉熵的定义。

交叉熵

交叉熵(Cross Entropy)主要衡量两个概率分布之间的差异性。交叉熵可在神经网络中作为损失函数，有：
$$H(P^{\ast }|P)=-\sum _i{P}^{\ast }(i)\log P(i)\text{\hspace{1em}(13)}$$
其中$P^{\ast }$表示真实分布；$P$表示预测分布；$i$表示分布中的所有类别。

KL散度和交叉熵

我们已经了解了KL散度和交叉熵，我们本小节来看它们之间的关系。

我们知道，交叉熵可以用来衡量预测分布和真实分布的差异(距离)。我们观察到的样本都是由真实分布产生的，所以我们可以这样描述KL散度：
$$D_{KL}(P^{\ast }||P)=D_{KL}\left(P^{\ast }(y|x_i)||P(y|x_i;\theta \right)\text{\hspace{1em}(14)}$$
其中$P^{\ast }$是真实分布，$P$是我们的预测分布；$x_i$是第$i$个样本，$y$是其对应的标签；$\theta$是模型的参数。
$$\begin{array}{rl}{D}_{KL}(P^{\ast }||P)& =\sum _y{P}^{\ast }(y|x_i)\log \frac{P^{\ast }(y|x_i)}{P(y|x_i;\theta )}\\ & =\sum _y{P}^{\ast }(y|x_i)\left[\log P^{\ast }(y|x_i)-\log P(y|x_i;\theta )\right]\\ & =\sum _y{P}^{\ast }(y|x_i)\log P^{\ast }(y|x_i)-\sum _y{P}^{\ast }(y|x_i)\log P(y|x_i;\theta )\end{array}\text{\hspace{1em}(15)}$$
观察上面最终的式子，其中$P^{\ast }(y|x_i)\log P^{\ast }(y|x_i)$与参数$\theta$无关，实际上是真实分布的信息熵，是一个常数；而 $-P^{\ast }(y|x_i)\log P(y|x_i;\theta )$就是我们熟悉的交叉熵的式子。

如果看不明白的话，或者我们换一种写法：$D_{KL}(P^{\ast }||P)=-S(P^{\ast })+H(P^{\ast },P)$，$S(P^{\ast })$是$P^{\ast }$的信息熵；$H(P^{\ast },P)$是交叉熵，KL散度 = 交叉熵 - 熵

因此，我们最小化关于参数$\theta$的KL散度，就相当于最小化式$(15)$中的第二项，即：
$$\arg \underset{\theta }{\min }{D}_{KL}(P^{\ast }||P)\equiv \arg \underset{\theta }{\min }-\sum _i{P}^{\ast }(y|x_i)\log P(y|x_i;\theta )\text{\hspace{1em}(16)}$$
即
$$\arg \underset{\theta }{\min }{D}_{KL}(P^{\ast }||P)\equiv \arg \underset{\theta }{\min }H(P^{\ast },P)\text{\hspace{1em}(17)}$$
因此，在机器学习中，我们要评估预测模型和真实模型之间的差距，可以使用KL散度，而KL散度中的信息熵那一部分不变，所以只需要关注交叉熵就可以了。

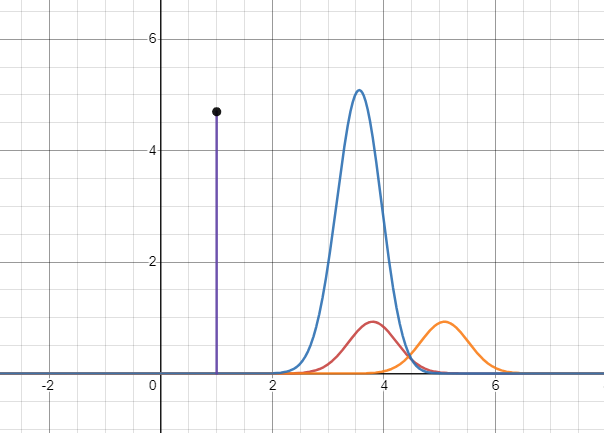
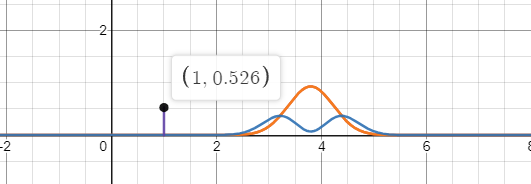
基于KL散度恒不小于零的特性,博主找到了一个很好的图示：

红色曲线代表真实概率分布；橙色曲线代表预测概率分布；紫线代表蓝色曲线下的面积，代表这两个分布的交叉熵。

交叉熵的大小与预测分布和真实分布的偏离程度相关。

当两个分布重叠时，此时交叉熵最小，为真实分布的信息熵。

交叉熵损失

在机器学习中，我们需要评估标签值$y$和预测值$\hat{y}$之间的差距，我们知道只需要关注交叉熵。一般在机器学习中直接用交叉熵做损失函数来评估模型。

$$loss=-\sum _{j=1}^n{y}_j\log {\hat{y}}_j\text{\hspace{1em}(18)}$$
这里$y_j$是真实样本的标签；${\hat{y}}_j$是预测值，通常是一个概率；$n$是分类的个数；因此这是针对单个样本的情况，如果对于批量样本，那么交叉熵计算公式为：
$$\mathcal{L}=-\sum _{i=1}^m\sum _{j=1}^n{y}_{ij}\log {\hat{y}}_{ij}\text{\hspace{1em}(19)}$$
其中$m$是样本数；$n$是分类数。

二分类

有一种特殊问题，即分类数为$2$，就是二分类问题。对于这种问题，由于$n=2$，$y_1=1-y_2$，${\hat{y}}_1=1-{\hat{y}}_2$，所以交叉熵可以简化为：
$$loss=-\left[y_1\log {\hat{y}}_1+(1-y_1)\log (1-{\hat{y}}_1)\right]\text{\hspace{1em}(20)}$$
对于批量样本的交叉熵为：
$$\mathcal{L}=-\sum _{i=1}^m\left[y_i\log {\hat{y}}_i+(1-y_i)\log (1-{\hat{y}}_i)\right]\text{\hspace{1em}(21)}$$
通常对于二分类问题，记正例为$1$，负例为$0$。因此上式的两个相加项只会有一个存在。

多分类

常见的是多分类问题，即分类数$n\ge 3$。多分类问题对于批量样本的交叉熵损失即为式$(19)$：
$$\mathcal{L}=-\sum _{i=1}^m\sum _{j=1}^n{y}_{ij}\log {\hat{y}}_{ij}$$
这里有必要指出的是，对于多分类问题，标签值一般采用独热编码，预测值在输出之前会经过Softmax转换为概率分布。这样交叉熵损失只会关注预测正确的类别的概率。

这种特性使得代码编写也比计较直观。

均方误差和交叉熵

我们知道，线性回归的损失函数是均方误差，而逻辑回归的损失函数为交叉熵损失。为什么呢？

先看逻辑回归为什么用交叉熵损失而不是均方误差。

逻辑回归其实是分类问题，输出的是一个概率，交叉熵就是用于衡量概率距离的函数，所以选用交叉熵损失。如果把概率值看成是一个数值的话，也可以用均方误差啊。那到底为什么呢？

我们可以从均方误差和交叉熵的函数图形入手。

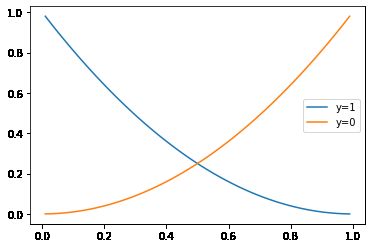
以二分类问题为例，先看交叉熵的函数图形。

import numpy as np
import matplotlib.pyplot as plt

def cross_entropy(y_hat, y):
  return -np.log(y_hat) if y == 1 else -np.log(1 - y_hat)
 
y_hat = np.arange(0.01,1,0.01)

plt.plot(y_hat, cross_entropy(y_hat, 1), label='y=1')
plt.plot(y_hat, cross_entropy(y_hat, 0), label='y=0')
plt.legend()
plt.show()

其中蓝线代表真实标签$y=1$时的交叉熵损失函数图形，橙线代表真实标签$y=0$时的图形。横坐标代表预测值，纵坐标代表损失值。

可以看到，当$y=1$时(蓝线)，如果预测的越正确(预测值与1越近)，则损失(惩罚)越小，在越接近0的位置，损失越大。

反过来，当$y=0$时(橙线)，如果预测的越正确(预测值与0越近)，则损失越小，在越接近1的位置，损失越大。

我们来看下，当$y=1$时，预测结果为$\hat{y}=0.1$时的损失：

> cross_entropy(0.1, 1)
2.3025850929940455

大约是$2.3$。

我们再来看均方误差的图形：

def mse(y_hat, y):
  return (y - y_hat)**2
 
plt.plot(y_hat,mse(y_hat, 1) , label='y=1')
plt.plot(y_hat, mse(y_hat, 0), label='y=0')
plt.legend()

其中蓝线代表真实标签$y=1$时的均方误差损失函数图形，橙线代表真实标签$y=0$时的图形。横坐标代表预测值，纵坐标代表损失值。

上面纵轴最大值也只是$1.0$，整个函数图像看起来也没有特别大的梯度。

我们也来看下，当$y=1$时，预测结果为$\hat{y}=0.1$​时的损失：

> mse(0.1, 1)
0.81

其损失值也不大，如果选用均方误差作为逻辑回归的损失函数，很可能训练不起来。

这样我们就明白了为什么逻辑回归要选择交叉熵。

我们再来看线性回归为什么不选择交叉熵。直接说结论，假设概率分布为高斯分布的情况下，采用交叉熵损失等同于采用均方误差损失。相关证明可以网上查找。

交叉熵损失的梯度

这里以多分类问题为例，拷贝了博主之前的另一篇文章Softmax与Cross-entropy的求导。

softmax函数为:

$${\hat{y}}_i=\frac{e^{z_i}}{{\sum }_{k=1}^K{e}^{z_k}}$$

这里$K$是类别的总数，接下来求${\hat{y}}_i$对某个输出$z_j$的导数,
$$\frac{\partial {\hat{y}}_i}{\partial z_j}=\frac{\partial \frac{e^{z_i}}{{\sum }_{k=1}^K{e}^{z_k}}}{\partial z_j}$$

这里要分两种情况,分别是$i=j$与$i\ne j$。当$i=j$时,$e^{z_i}$对$z_j$的导数为$e^{z_i}$，否则当$i\ne j$时，导数为$0$。

当$i=j$，
$$\begin{array}{rl}\frac{\partial {\hat{y}}_i}{\partial z_j}& =\frac{e^{z_i}\cdot {\sum }_{k=1}^K{e}^{z_k}-e^{z_i}\cdot e^{z_j}}{({\sum }_{k=1}^m{e}^{z_k}{)}^2}\\ & =\frac{e^{z_i}}{{\sum }_{k=1}^m{e}^{z_k}}-\frac{e^{z_i}}{{\sum }_{k=1}^m{e}^{z_k}}\cdot \frac{e^{z_j}}{{\sum }_{k=1}^m{e}^{z_k}}\\ & ={\hat{y}}_i-{\hat{y}}_i^2={\hat{y}}_i(1-{\hat{y}}_i)\end{array}$$

当$i\ne j$，
$$\begin{array}{rl}\frac{\partial {\hat{y}}_i}{\partial z_j}& =\frac{0\cdot {\sum }_{k=1}^K{e}^{z_k}-e^{z_i}\cdot e^{z_j}}{({\sum }_{k=1}^m{e}^{z_k}{)}^2}\\ & =-\frac{e^{z_i}}{{\sum }_{k=1}^m{e}^{z_k}}\cdot \frac{e^{z_j}}{{\sum }_{k=1}^m{e}^{z_k}}\\ & =-{\hat{y}}_i{\hat{y}}_j\end{array}$$

损失函数$L$为:
$$L=-\sum _k{y}_k\log {\hat{y}}_k$$

其中$y_k$是真实类别，相当于一个常数，接下来求$L$对$z_j$的导数

$$\begin{array}{rl}\frac{\partial L}{\partial z_j}& =\frac{\partial -({\sum }_k{y}_k\log {\hat{y}}_k)}{z_j}\\ & =\frac{\partial -({\sum }_k{y}_k\log {\hat{y}}_k)}{\partial {\hat{y}}_k}\frac{\partial {\hat{y}}_k}{\partial z_j}\\ & =-\sum _k{y}_k\frac{1}{{\hat{y}}_k}\frac{\partial {\hat{y}}_k}{z_j}\\ & ={\left(-y_k\cdot {\hat{y}}_k(1-{\hat{y}}_k)\frac{1}{{\hat{y}}_k}\right)}_{k=j}-\sum _{k\ne j}{y}_k\frac{1}{{\hat{y}}_k}(-{\hat{y}}_k{\hat{y}}_j)\\ & =-y_j(1-{\hat{y}}_j)-\sum _{k\ne j}{y}_k(-{\hat{y}}_j)\\ & =-y_j+y_j{\hat{y}}_j+\sum _{k\ne j}{y}_k({\hat{y}}_j)\\ & =-y_j+\sum _k{y}_k({\hat{y}}_j)\\ & =-y_j+{\hat{y}}_j\\ & ={\hat{y}}_j-y_j\end{array}$$

这里用到了${\sum }_k{y}_k=1$

Reference

1. 如何理解信息熵

2. 损失函数是如何设计出来的

3. Softmax与Cross-entropy的求导