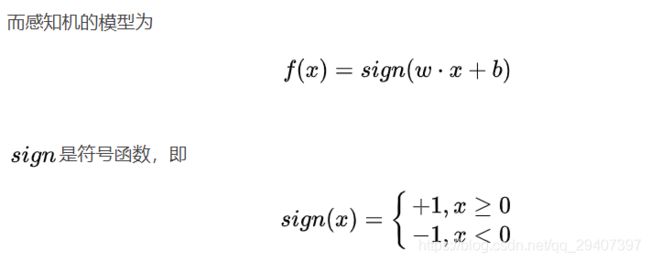【统计学习方法】第二章 感知机和课后习题

第二章 感知机

在学习一个模型的时候应该问：

• 模型的适用条件
• 要解决什么问题
• 对应统计学习方法的三个要素，假设空间，策略，算法
  感知机要解决的问题是二分类问题，假设是数据是可分的。

2.1 感知机模型

符号说明：
输入空间：$X\subseteq R^n$
输入变量：$x\in X$
输出空间：$Y=\{+1,-1\}$
输出变量：$y\in \{+1,-1\}$
假设空间：
$$f(x)=\mathrm{sign}(w\cdot x+b)$$
其中sign是符号函数

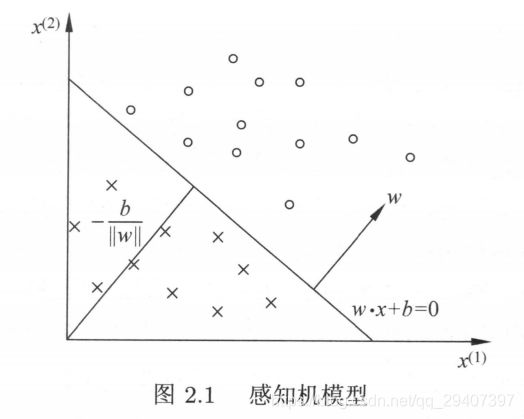
2.2 感知机的学习策略

损失函数：
误分类点到超平面的距离：
$$L(w,b)=-\sum _{x_i\in M}{y}_i\left(w\cdot x_i+b\right)$$
其中M是误分类点的集合。

2.4 感知机学习算法

2.4.1 随机梯度下降：

输入：
训练数据集$T=\left[\left(x_1,y_1\right),\dots ,\left(x_N,y_N\right)\right)$
学习率$\eta$

1. 选取初值$w_0,b_0$
2. 在训练集中选取数据$\left(x_i,y_i\right)$
3. 如果$y_i\left(w\cdot x_i+b\right)\le 0$
   $w:=w+\eta y_i{x}_i$
   $b:=b+\eta y_i$
4. 转至2，直到训练集中没有误分类的点

输出w,b

2.4.2 感知机模型的对偶形式

感知机模型的对偶形式
$$\begin{array}{c}f(\chi )=\mathrm{sign}\left({\sum }_{j=1}^N{\alpha }_j{y}_j{x}_j\cdot x+b\right)\\ \alpha ={\left({\alpha }_1,\cdots {\alpha }_N\right)}^T\end{array}$$

算法：
输入：
训练数据集$T=\left[\left(x_1,y_1\right),\dots ,\left(x_N,y_N\right)\right)$
学习率$\eta$
1.初值$\alpha :=0,b:=0$
2.在训练集中选取数据$\left(x_i,y_i\right)$
3.如果$y_i\left({\sum }_{j=1}^N{\alpha }_j{y}_j{x}_j\cdot x+b\right)\le 0$
${\alpha }_i:={\alpha }_i+\eta$
$b:=b+\eta y_i$
4. 转至2，直到训练集中没有误分类的点

输出w,b

对于随机梯度下降来说，对偶形式更新参数要少。

习题

2.1 Minsky与Papert指出：感知机因为是线性模型，所以不能表示复杂的函数，如异或（XOR）。验证感知机为什么不能表示异或。
首先看一下异或：
简单理解，如果两个数a和b进行异或操作。如果a、b两个值不相同，则异或结果为1。如果a、b两个值相同，异或结果为0。