Introspective Distillation for Robust Question Answering 论文笔记

写在前面
  这是一篇关于VQA de-bias的文章，出自获得2021年的CCF优秀博士论文之一的牛玉磊大神。之前有一篇CF-VQA也是这位大佬的工作。本文看问题角度与其他方法不一样，结合了知识蒸馏的部分，不知道咋想出来的？

• 论文地址：Introspective Distillation for Robust Question Answering
• 代码地址：Github，开源了但没完全开~
• 收录于：NeurIPS 2021

一、Abstract

  开始点出语言bia普遍存在于QA模型中，引出本文的VQA和阅读理解任务。接着指出现有的de-bias的方法精度高的原因：提前知道了测试集数据的分布，换句话说，能够利用测试集的bias。本文提出一种新颖的de-bias方法——IntroD，能够在这两种任务中发挥出最大的作用。本文主要贡献在于通过introspecting内省是否训练样本符合ID的事实或者OOD的事实，从而融合ID和OOD的bias。实验在VQAv2，CPv2，SQuAD数据集进行，在牺牲少量精度的情况下，能够维持OOD的性能，甚至超过了之前的那些no-bias方法。

二、引言

  引入问答的基础概念→模型利用数据集中的bias→在out-of-distribution(OOD)的数据分布中性能下降→本文认为虽然有一些方法提升了ID和OOD的性能，但是源于大部分的模型都存在假设：训练和测试分布非常不同甚至完全相反，所以模型可能在ID内面临严重的性能下降？能解释通吗？理论上可以，因为这些方法降低了原来模型在ID内的性能。这就引出本文的主题了，能够使得模型同时在ID和OOD分布上的精度都很高吗？下图为作者给出的证据：

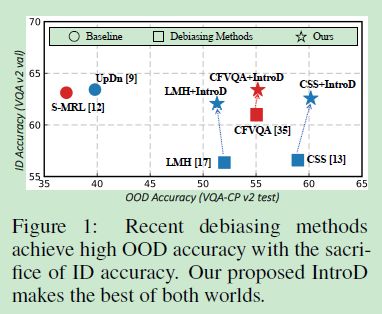
  接下来突出本文的核心，建立一个鲁棒性的模型能够同时在ID和OOD上保持足够的精度。而这一点使得作者认为模型需要公平的利用这两种分布的bias。因此，作者提出introD来融合/混合这两种bias。
  综的框架：两种专家模型：ID-教师，OOD-教师，每一个教师负责捕捉相应的bias，再蒸馏出一个内省学术来学习这两类教师，而这存在三种情况：

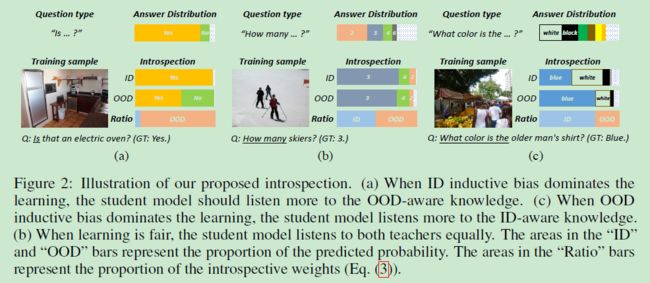
• 如果ID-bias > OOD-bias, 那么 ID-teacher < OOD-teacher，即ID教师过拟合，所以学生需要从OOD教师中学到更多。
  这种情况存在于ID教师的损失
• 如果ID-bias < OOD-bias, 那么 ID-teacher > OOD-teacher，即OOD教师过拟合，所以学生需要从ID教师中学到更多。
  这种情况存在于ID教师的损失
• 如果ID-bias ≈ OOD-bias, 那么 ID-teacher ≈ OOD-teacher，即两个教师正常拟合，所以学生需要同等地学习两位教师。
  这种情况存在于ID教师的损失≈ OOD教师的损失时，即上图b所示。

接下来就是讲的蒸馏了，在这部分之前，主要问题就是教师模型的获得，特别是OOD的教师，因为OOD分布在训练过程中不可视。然后作者也是用了自己之前发表的文章内容，即反事实VQA，CF-VQA。根据因果模型来进行反事实推理，从而想象出未知的OOD分布，从而获得OOD教师模型。另外，作者表明：本文方法成功的来源之处在于因果反省，而非简单的ensemble嵌入。

三、Related work

3.1 视觉问答

  概念的介绍→bias的存在→VQA-CP数据集→影响VQAv2数据集的精度，目前仍有待解决。

3.2 Extractive Question Answering

  该任务旨在回答所给自然语言上下文(段落)的问题，同时是个位置预测的分类问题，因此这种分类问题也存在bias，从而引入数据集SQuAd用于评估语言模型是否存在位置bias。

3.3 Ensemble-based methods for debiasing

  该方法显式地构建并包含了捷径bias，这种捷径能够通过一个单独的分支或者统计先验进行捕捉。这些方法虽在OOD的分布上取得了很高的精度，但是在ID分布上确是降低了很多精度，原因在于这些方法是根据训练集和测试集的分布有着完全不同甚至相反的比例这种假设来进行训练的。本文采用之前提出的CF-VQA和ID-OOD教师模型，实现了ID-OOD评估的平衡。

3.4 Knowledge Distillation

  知识蒸馏将教师的知识蒸馏到一个小型的学生模型上，本文提出的Introspection反省与自蒸馏相关，只不过自蒸馏是将学生模型自身作为下一次训练中的教师。其不同之处：自蒸馏仍处于ID分布内，并不存在对于看见的事实或者看不见的反事实进行比较推理，这也是为啥本文的自反省引入了融合/混血知识而不是直接copy自蒸馏。另外有一点不同在于本文的蒸馏并未使用一个固定的权重超参数，而是基于反省角度的权重，并不需要额外的超参数选择。

四、内省蒸馏

  输入为视觉或者自然文本$C=c,Q=q$，QA模型旨在产生答案$A=a$，本质为多分类问题，即$a\in \mathbb{A}$。作者提出的IntroD旨在平等地融合ID和OOD-bias，该方法由三个模块组成：

• casual teacher：用于捕捉ID和OOD-bias
• introspection：用于融合/混合这两种不同的bias
• distillation：用于蒸馏出鲁棒性的学生模型

4.1 ID-Teacher and OOD-Teacher

  由于无法得到OOD分布，所以没办法得到OOD教师模型，这里引入CF-VQA方法，采用反事实推理得到OOD教师模型。同时ID教师也能近似地通过事实推理使用相同的casual模型来得到。
  根据反事实推理，casual模型能够想象出OOD分布，因此使用相同的casual模型部署ID和OOD教师。通过事实推理，casual模型能够预测出答案$P^{ID}$，该答案包含了ID-bias；通过反事实推理，casual模型能够估计直接的影响来排除掉bias，并产生反事实的预测$P^{OOD}$，即，非直接的影响或者自然的非直接的影响反映着看不见的OOD分布。教师模型采用交叉熵损失在ID数据上训练，并未分别训练ID和OOD教师模型。

4.2 Introspection of Inductive Bias

   Introspection 模块首先测试是否模型过度利用了ID或者OOD的bias，如果ID-bias主导了学习，那么学生模型就应该倾向于OOD的教师模型。因此引出两个问题，如何定义“主导”和“更倾向”，换句话说，如何反省和权衡这两种bias。

4.2.1 Introspecting the bias

  通过比较ID和OOD教师的预测来反省bias的影响，如果ID内的主导了样本的学习，那么ID教师的置信度将会大于OOD教师的，用公式表示如下：
$$s^{\mathrm{I}\mathrm{D}}=\sum _{a\in {\mathcal{A}}^{\mathrm{G}\mathrm{T}}}{P}^{\mathrm{I}\mathrm{D}}(a),s^{\mathrm{O}\mathrm{O}\mathrm{D}}=\sum _{a\in {\mathcal{A}}^{\mathrm{G}\mathrm{T}}}{P}^{\mathrm{O}\mathrm{O}\mathrm{D}}(a),$$
其中${\mathcal{A}}^{\mathrm{G}\mathrm{T}}$为gt answer, $S$得分反映了训练样本与bias的契合程度。如果$s^{\mathrm{I}\mathrm{D}}>s^{\mathrm{O}\mathrm{O}\mathrm{D}}$，那么样本的学习由ID-bias主导反之亦然。接下来就是$s^{\mathrm{I}\mathrm{D}},s^{\mathrm{O}\mathrm{O}\mathrm{D}}$的确定了，表示如下：
$$\begin{array}{rl}{s}^{\mathrm{I}\mathrm{D}}& =\frac{1}{XE\left(P^{\mathrm{G}\mathrm{T}},P^{\mathrm{I}\mathrm{D}}\right)}=\frac{1}{{\sum }_{a\in \mathcal{A}}-P^{\mathrm{G}\mathrm{T}}(a)\log P^{\mathrm{I}\mathrm{D}}(a)},\\ s^{\mathrm{O}\mathrm{O}\mathrm{D}}& =\frac{1}{XE\left(P^{\mathrm{G}\mathrm{T}},P^{\mathrm{O}\mathrm{O}\mathrm{D}}\right)}=\frac{1}{{\sum }_{a\in \mathcal{A}}-P^{\mathrm{G}\mathrm{T}}(a)\log P^{\mathrm{O}\mathrm{O}\mathrm{D}}(a)},\end{array}$$其中$P^{GT}$为真实标签，采用交叉熵来训练比之前的相加效果要好。

4.2.2 Weighting the bias

  利用知识的权重求和来融合/混合ID和OOD的知识，目的在于公平的混合ID或者OOD的bias。因此就有前面说的三种情况，如果$s^{\mathrm{I}\mathrm{D}}>s^{\mathrm{O}\mathrm{O}\mathrm{D}}$，那么学生模型就应该从OOD教师模型中学习的更多，因此就要增加$w^{OOD}$，使得$w^{OOD}>w^{ID}$。类似的，当$s^{\mathrm{I}\mathrm{D}}<s^{\mathrm{O}\mathrm{O}\mathrm{D}}$，则要令$w^{OOD}<w^{ID}$，而相应的知识权重需要设置成与得分相反的比例，即$w\propto s^{-1}$，本文通过尺度将权重缩放至0，1：
$$w^{\mathrm{I}\mathrm{D}}=\frac{{\left(s^{\mathrm{I}\mathrm{D}}\right)}^{-1}}{{\left(s^{\mathrm{I}\mathrm{D}}\right)}^{-1}+{\left(s^{\mathrm{O}\mathrm{O}\mathrm{D}}\right)}^{-1}}=\frac{s^{\mathrm{O}\mathrm{O}\mathrm{D}}}{s^{\mathrm{I}\mathrm{D}}+s^{\mathrm{O}\mathrm{O}\mathrm{D}}},w^{\mathrm{O}\mathrm{O}\mathrm{D}}=1-w^{\mathrm{I}\mathrm{D}}=\frac{s^{\mathrm{I}\mathrm{D}}}{s^{\mathrm{I}\mathrm{D}}+s^{\mathrm{O}\mathrm{O}\mathrm{D}}}$$
  作者之后利用CF-VQA作为教师模型绘制出了VQA-CPv2及VQAv2训练数据集的$w^{ID}$分布情况：

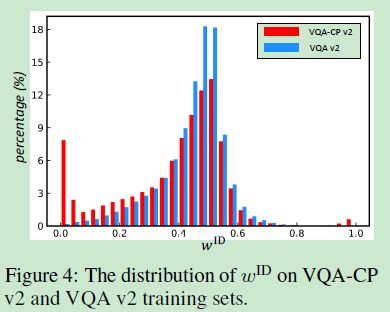
  对于上图来说，$w^{ID}$越小则说明ID-bias越大，对上图的三种观察发现：

• 所有数据集的$w^{ID}$在0.5左右，说明大多数样本仍然可以无bias的学习预测。
• 所有的数据集bias分布都呈现一种左偏的趋势，随着$w^{ID}$在0.5范围内减小，两种数据集的差异越发明显。这表明了VQA模型倾向于利用VQA-CPv2中不平衡的bias，而不是平衡的样本部分。换句话说，VQA-CP数据集是在鼓励模型学习语言bias(这也是在佐证作者提出的观点)。在没有这些记忆先验的情况下，VQA模型无法正确回答极端情况下的问题。

作者也定义了一种stochastic hard variant（随机硬变体?）来加权bias：
$$w^{\mathrm{I}\mathrm{D}}=\{\begin{array}{ll}1& ,\text{ if }{s}^{\mathrm{I}\mathrm{D}}\le s^{\mathrm{O}\mathrm{O}\mathrm{D}}\\ 0& ,\text{ otherwise }\end{array}$$
  这样一种公式使得学生模型能够完整学习OOD教师模型中的大多数样本并维持其OOD性能。接下来，融合/混合这两种知识：
$$P^{\mathrm{T}}=w^{\mathrm{I}\mathrm{D}}\cdot \text{ ID-Knowledge }+w^{\text{OOD }}\cdot \text{ OOD-Knowledge. }$$其中$\text{ ID-Knowledge }$为gt lables $P^{GT}$，$\text{ ID-Knowledge }$为OOD预测$P^{OOD}$的近似。

4.2.3 Distillation of Fair Knowledge

  学生模型的训练：
$$\mathcal{L}=KL\left(P^{\mathrm{T}},P^{\mathrm{S}}\right)=\sum _{a\in \mathcal{A}}{P}^{\mathrm{T}}(a)\log \frac{P^{\mathrm{T}}(a)}{P^{\mathrm{S}}(a)}$$其中$P^S$为学生模型，例如UpDn，BERT等模型。与学生模型不同，教师模型还嵌入了一个单独的分支来构成捷径bias，所以相比于casual教师模型，学生模型能够更有效的利用参数和推理速度。在蒸馏时固定casual模型，仅更新学生模型。

五、Experiments

5.1 Visual QA

5.1.1 数据集

  VQA v2；VQA-CP v2

5.1.2 Metric and setting

  采用标准的VQA评估方法，采用两种设置，ID→VQA v2，OOD→VQA-CP test，还有在VQA-CP v2测试集上及VQA v2验证集上的HM调和平均数。

5.1.3 Methods

  反事实教师：RUBi，LMH，CSS，CF-VQA
  Backbone：UpDn，S-MRL
  软变体(soft variant)权重：LMH，CSS，RUBi-CF，CF-VQA
  硬变体(hard variant)权重：RUBi

5.1.4 Overall results

5.1.5 Ablation studies

  本文的消融实验旨在解决下列问题：

Can we use the predicted probability of the ground-truth answer (“Prob.” for short) as the matching scores? Better not.

  对比2，3列，划不来。

Can the student learn more from the more accurate teacher, i.e. $w\propto s$？No.

Can the student equally learn from ID and OOD teachers, i.e. $w^{ID}=w^{OOD}=0.5$? No.

  如上图。

Can the student only learn from OOD-teacher? Yes, but worse than IntroD.

  如上图。

Should we use the hard or soft variant to calculate the knowledge weights? It depends on the debiasing ability of the causal teacher.

Can we use the $\text{ID-Prediction}{P}^{ID}$ as the $\text{ID-Knowledge}$? No.

Can we ensemble the two teacher models and directly use that without distillation? In other words, is IntroD just an ensemble method? No.

5.2 Extractive QA

5.2.1 Dataset and settings

  SQuAD

5.2.2 Metrics and method.

  exact match (EM) 、F1 score
  Backbone：XLNet、BERT
  casual教师：LM
  知识权重计算：hard variant硬变体

5.2.3 Results

六、Conclusion

  本文提出了IntroD，在ID和OOD-bias分布上能够平衡bias，采用VQA和extract QA评估本文的方法。大致步骤为采用casual教师来评估ID和OOD的bias，然后内省是否这两种bias主导了学信息，之后公平的融合/混合这两种bias，并将其蒸馏到学生模型上。实验证明效果很高，IntroD的主要限制在于OOD的性能极度依赖于OOD教师模型。

附录

A1、Causal QA Model

  推荐查看CF-VQA论文

A2、Datasets

  VQA和Extract QA数据集的介绍

A3、Training Details

A3.1 Implementation of LMH

  RTX 2080Ti， Batch 512。

A3.2 Implementation of CSS

  RTX 2080Ti， Batch 512。

A3.3 Implementation of RUBi

  RTX 2080Ti， Batch 256，22Epoch，$lr=1.5\times 10^{-4},6\times 10^{-4}$ 7epoch，14个epoch x0.25/2epoch

A3.4 Implementation of CF-VQA

  RTX 2080Ti， Batch 256。

A3.5 Implementation of LM

2个RTX 2080Ti， Batch 10，12，$lr=3\times 10^{-5}$

A4、Additional Experimental Results

A4.1 Compared with State-of-the-art Methods

A4.2 Evaluations on Feature Quality

A4.3 Error Bars

  表13。

A4.4 Results on Natural Language Inference

A5、Social Impacts

  提出的方法使得VQA模型更鲁棒，但是非端到端的方法比较耗时。
写在后面
  本文为消除VQA任务中的bias提供了另一种角度，不光只是在VQA-CPv2数据集上进行试验，同时也在VQAv2上进行对比实验，角度新奇。另外作者用了之前发表的文章，使得本文一脉相承，确实思路很好，缺点作者也说了方法需要两段式训练，费时。另外我个人吐槽下，文中这些对比实验真的写的比较繁琐，有点头大。