当我们需要对数据集进行聚类时,我们可能首先研究的算法是 K means, DBscan, hierarchical clustering 。那些经典的聚类算法总是将每个数据点视为一个点。但是,这些数据点在现实生活中通常具有大小或边界(边界框)。忽略点的边缘可能会导致进一步的偏差。RVN算法是一种考虑点和每个点的边界框的方法。
RVN 的灵感来自一家家具公司的商业案例。他们的工作是按生活方式对家具进行分类,由于每件家具都有不同的形状和大小,而一些家具是否重叠比彼此之间的距离更关键,所以创建了可以考虑每个点大小的 RVN 算法,相信该算法可以进一步在其他领域实现,例如生态系统和像素聚类。
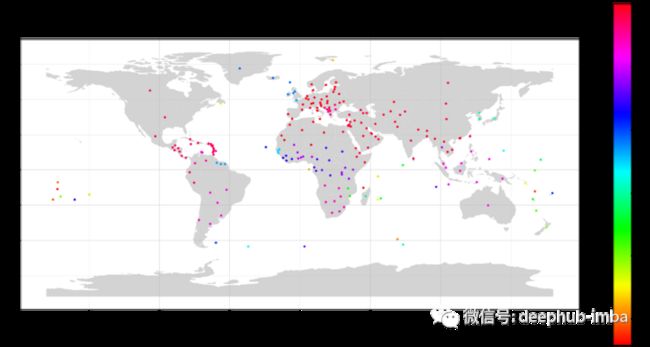
世界地图示例 - K means
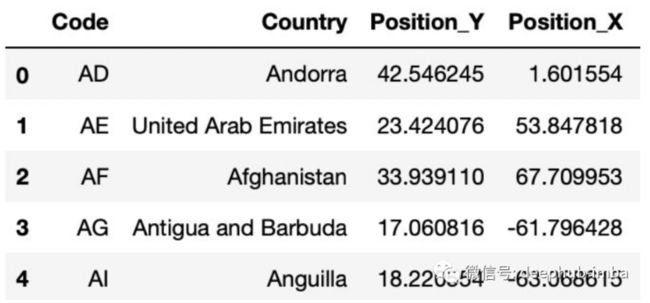
当需要对地球上所有国家进行聚类时,首先需要每个国家的坐标(经度和纬度)。
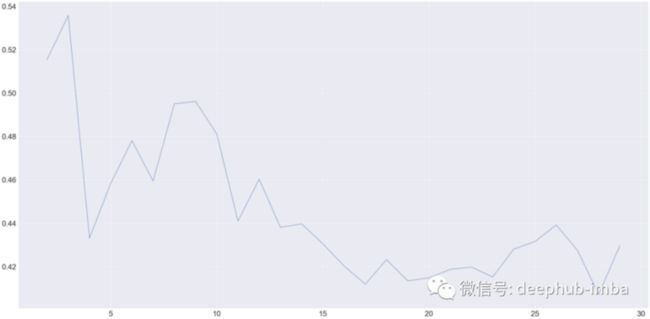
然后可以使用 K mean 或其他算法来调整最佳簇数量或找到最佳 eps 进行DB scan。我们将使用 K mean作为样例
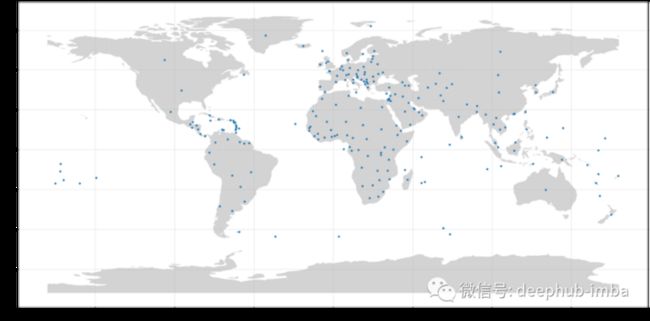
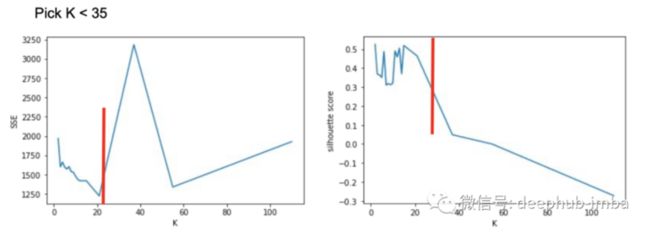
根据上图,我们选择k=3。
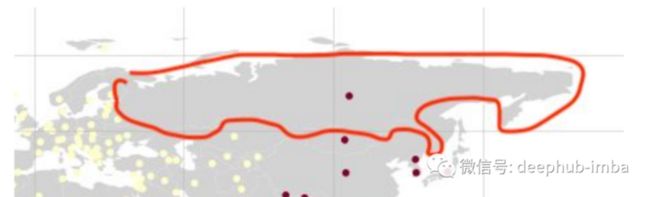
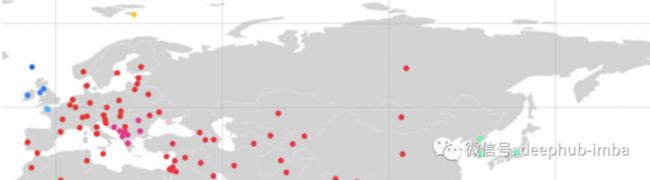
看起来不错!但是我们可以注意到一些国家的一些问题,比如俄罗斯。
可以看到俄罗斯与其他亚洲国家聚集在一起。原因是代表俄罗斯位置的点更靠近其他亚洲国家。如果我们把这一点再左一点,俄罗斯就会聚集到左边。
通过这个例子定义每个点的位置对我们的结果有很大的影响。
RVN 算法
下面介绍一下RVN算法的基本逻辑。
数据要求:每个点的上限和下限
初始化
- 初始化n个簇(数据大小为n),每个点为一个簇
- 计算每个簇的半径(使用上限和下限)
迭代
- 检查所有重叠点。(范围重叠)
- 将所有重叠点分组为同一个簇
- 更新每个簇的质心和半径
停止策略
- 如果没有重叠组,则停止
- Stop by k :设置一个 K 并在总聚类低于 K 时停止算法(k mean概念)
- 其他:所有大小的百分比,最近簇的距离
下面进一步演示这个算法。
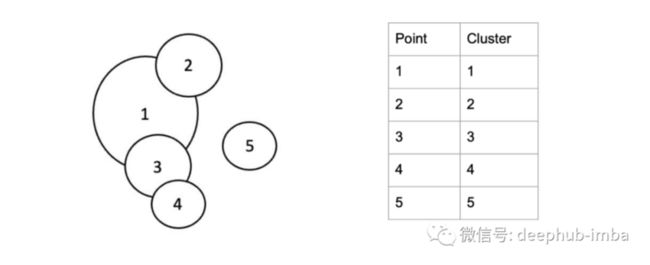
第 1 步:初始簇
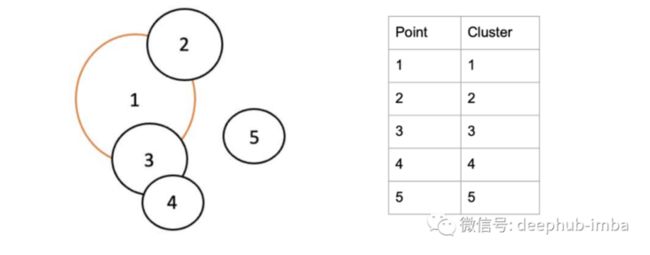
第 2 步:检查数据点1
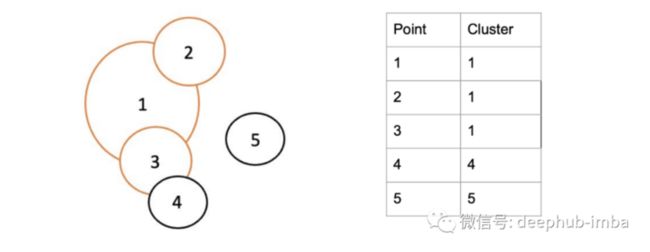
第 3 步:将点 1 和 3 更新到簇 1
第 4 步:检查数据点 2,已更新
第 5 步:检查数据点3,更新数据点4
第 6 步:检查数据点 5,没有重叠点
第 7 步:更新质心和边界。第一次迭代结束
第 8步:开始第二次迭代,检查组 1 并将点 5 更新为点 1
第 9 步:检查数据点 5,不更新任何内容
第10步:更新质心和边界,结束第二次迭代
簇扩展方法
有一种不可避免的情况就是没有重叠点但我们仍然希望将点分组在一起。
如果我们根据基本规则停止算法,可能会有太多的簇。所以提供三种可能的解决方案。
Naive:逐渐将所有半径增加一个常数,以便两个最近的簇相互重叠(速度快因为所有组的半径同时增加,但可能会导致偏差)
Approximate:将两个最近的簇组合在一起。(慢但偏差较小,因为其他簇的半径保持不变)
其他:按百分比增加半径,按随机数增加
RVN 算法 - 参数
在 RVN 算法中,一些参数需要调整才能找到最佳参数。
- 半径:如果数据集是二维的,会有四个候选半径,分别是x-upperbound_x、x-lowerbound_x、y-upperbound_y、y-lowerbound_y。我们对选项进行排序,以挑选出最好的选项或根据经验进行选择。
- 扩展速度:在没有重叠点的情况下,圆圈希望增长多快。
- K 的阈值:当总簇数小于 K 时,算法停止。(仅用于“按 K 逻辑停止”)
找到最好的 K
与 K means算法相同,我们需要找到最佳 K。对于任何聚类方法,通常有两种方法可以找到最佳 K。轮廓系数和平方误差之和(每个点和组质心)。由于我们使用边界框而不是点,直接应用轮廓系数和平方误差之和会导致偏差。
因此在计算轮廓系数和平方误差和时,我们可以为每个点(母点)创建四个额外的点(子点),并将它们分配到与母点相同的组中。子点的坐标是(x,上界y),(x,下界y),(上界x,y)和(下界x,y)。
因为子点和母点加在一起可以更好地表示每个母点的大小,所以我们可以通过轮廓系数和平方误差和得到更无偏的 K。
在深入研究案例之前,让我们再次回到世界地图。
世界地图示例 - RVN
除了每个国家的经度和纬度,我们还需要上限和下限。
我们在这个例子中跳过了 调优K 的部分,因为我们只想展示不同的结果。
让我们仔细看看俄罗斯。
我们可以看到,俄罗斯现在与周边所有国家都聚集在一起。
家具公司示例
现在我们回到最初的家具公司示例,我们有了一个平面图将使用 RVN 对所有家具进行聚类。
让我们找到最佳 K
结果
我们可以看到,虽然有些点非常接近较大的组,因为它们的范围不与较大的组重叠,但它们被认为是不同的簇。
Python 实现
以下github地址是 NVR 算法的实现
https://github.com/red574890/...
算法的挑战
数据收集:数据收集是该算法中最麻烦的部分,因为需要收集一个点的位置和边界框。
高维:理想情况下,该算法可以在高维空间上实现。但是目前还没有尝试将其应用于超过三个维度的数据。
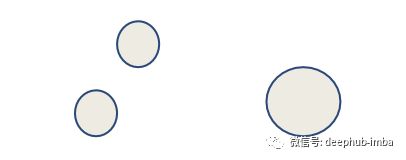
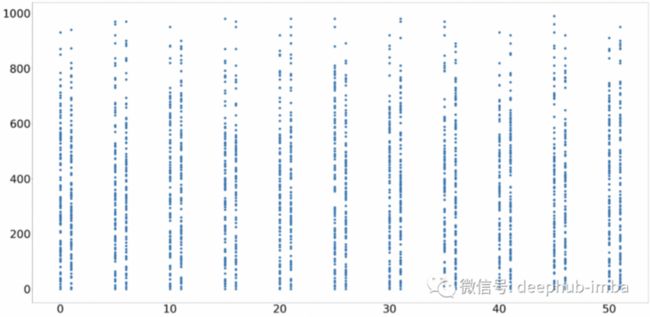
圆形假设:RVN 假设组扩展为一个圆形,这意味着如果一个簇增长,它将在所有方向上扩展相同的大小。但是,这种假设在某些情况下可能是错误的,如下图所示。
直观地说,这些数据应该分为 11 组。
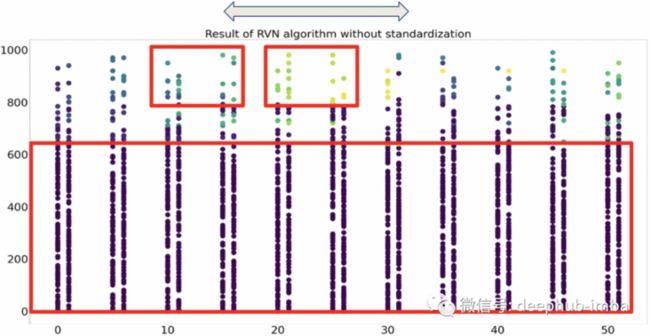
但是,由于 x 轴和 y 轴的尺度差异很大(y 范围从 0 到 1000,x 范围从 0 到 50),因此 RVN 算法的结果可能非常违反观察结果。
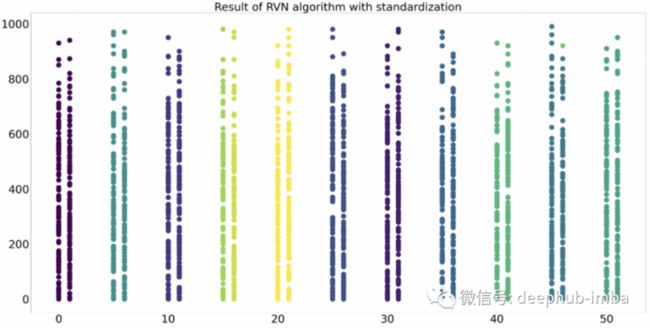
有一种可能的解决方案是标准化 x 范围或 y 范围。这个动作可以保证一个维度比另一个维度扩展得更快。
速度表现:不同的分组合并方式会导致算法的速度不同。目前没有最佳方法。
整体性能:该算法在平面图情况下比 DBscan和 K means效果更好。但是目前不知道 RVN 是否会在其他情况下表现更好。
未来
这是一种受家具行业平面图启发的全新算法。我真诚地希望我们能继续发展这种特殊的方法;因此,如果有人对改进或实施有任何疑问,请随时与我联系。
https://www.overfit.cn/post/cbf8eaf7ec2c44368bd25db40a6af68d
该算法由 Ray、Vamshi 和 Noah 创建
本文作者:Ray Hsu