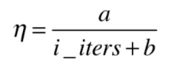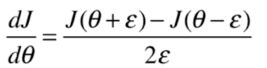梯度下降法
基于搜索的最优化算法,之前我们使用线性回归时最优的参数都是求正规方程解,但是很多时候求最优方程解时间复杂度非常的高或者是求不出最优方程解的,这个时候我们就用梯度下降法来得到最优参数
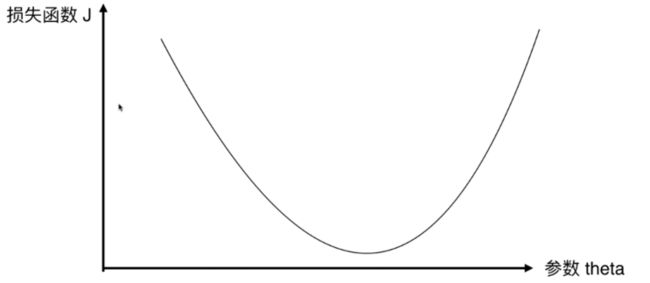
损失函数和θ的关系如图
最曲线方程中,导数代表斜率,决定了损失函数下降的方向
我们可以得到让斜率逐渐为0的公式
0=0-学习率*dj/d0
学习率
学习率决定了每次计算后跳跃的长度,如果太小梯度下降就会很缓慢需要耗费很多时间。而太大可能会导致梯度无法收敛甚至是梯度爆炸
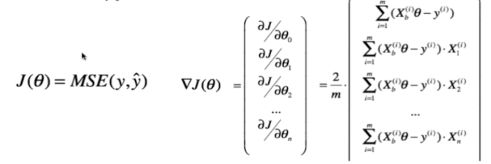
多元的0求导
代码实现
# 损失函数
def J(theta, X_b, y):
try:
return np.sum((y - X_b.dot(theta))**2) / len(X_b)
except:
return float('inf')
#计算theta的导数向量
def dJ(theta, X_b, y):
res = np.empty(len(theta))
res[0] = np.sum(X_b.dot(theta) - y)
for i in range(1, len(theta)):
res[i] = (X_b.dot(theta) - y).dot(X_b[:,i])
return res * 2 / len(X_b)
#X_b.T.dot(X_b.dot(theta) - y) * 2. / len(y) 可以用向量化后代替
#寻找最优theta
def gradient_descent(X_b, y, initial_theta, eta, n_iters = 1e4, epsilon=1e-8):
theta = initial_theta
cur_iter = 0
while cur_iter < n_iters:
gradient = dJ(theta, X_b, y)
last_theta = theta
#关键代码,梯度下降theta
theta = theta - eta * gradient
if(abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
break
cur_iter += 1
return theta
# 调用
X_b = np.hstack([np.ones((len(x), 1)), x.reshape(-1,1)])
initial_theta = np.zeros(X_b.shape[1])
eta = 0.01
theta = gradient_descent(X_b, y, initial_theta, eta)
批量梯度下降法
我们之前已知用的就是批量梯度下降法,每次进行梯度运算都需要用到所有样本,当样本数据量太大的时候是非常耗时的
随机梯度下降法
因为批量梯度下降法非常耗时,所以随机梯度下降法就是为了解决这个问题,在之前我们进行批量梯度下降法的时候最终结果要除以样本总数m,而随机梯度下降法是每次抽取一个来计算梯度方向以及大小。所以最终结果也不需要除以样本m
-
优缺点
缺点:梯度下降的过程中会有很多不确定性,有可能往梯度更高的地方,最终最优值可能精度相对批量梯度下降法较低
优点:可以节约非常多时间
使用随机梯度下降因为选择的样本是随机的可能导致在某样本已经下降到最佳值但是因为随机了新样本导致直接跳过最佳值。所以我们要选择合适的学习率来对这种情况做优化,当一开始的时候学习率可以比较大,但是多轮计算后为了为了保证新的随机样本对原来的梯度改变不会太大,我们要给他一个较小的学习率。所以就形成了随着计算次数越多,学习率越低。公式如下
a,b为超参数,i_iters是计算的次数。b的作用是为了起始学习率变化不会那么大。a的作用同b。b通常取50,a取5.
小批量梯度下降法
结合了批量梯度下降法和随机梯度下降法的优点,每次随机一部分样本进行梯度下降
源码
def dJ_sgd(theta, X_b_i, y_i):
return 2 * X_b_i.T.dot(X_b_i.dot(theta) - y_i)
def sgd(X_b, y, initial_theta, n_iters):
t0, t1 = 5, 50
def learning_rate(t):
return t0 / (t + t1)
theta = initial_theta
for cur_iter in range(n_iters):
rand_i = np.random.randint(len(X_b))
gradient = dJ_sgd(theta, X_b[rand_i], y[rand_i])
theta = theta - learning_rate(cur_iter) * gradient
return theta
X_b = np.hstack([np.ones((len(X), 1)), X])
initial_theta = np.zeros(X_b.shape[1])
theta = sgd(X_b, y, initial_theta, n_iters=m//3)
scikit-learn
from sklearn.linear_model import SGDRegressor
sgd_reg = SGDRegressor(n_iter=50)#n_iter所有样本都会被遍历,这个是所有样本遍历的次数
%time sgd_reg.fit(X_train_standard, y_train)
sgd_reg.score(X_test_standard, y_test)
梯度调试
在这之前我们计算梯度的时候每次都是对损失函数进行求导,得到斜率。在早期损失函数不确定的情况下自己求导其实是很麻烦的。所以我们也可以利用另外一种办法获得近乎相似的斜率。
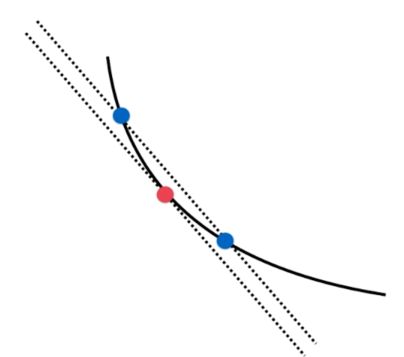
如图,我们可以在要求得点的周围找两个点,连接这两个点的直线的斜率会和要求的点的斜率相近。我们只要让这两个点逼近要求的点,那么斜率会越来越相近。可以得到两点求斜率公式
接下来我们只需要为每一个w利用这种方式求出他的导就可以了
比较
相比计算求导,这样求出斜率可以适用与任何函数,而不需要求导。但是消耗时间比较大。所以我们一般把它用来做测试,也就是可以用来检测我们对损失函数求导后的公式计算是否正确!