巴拉巴西:成功法则
一、导论
大家好,今天我们要换个话题,和往常一样,我们先从一个故事开始,这个故事和艺术有关。20世纪70年代,纽约当时的街头艺术以及涂鸦蓬勃发展,并且成为了一种艺术形式。1977年,一种非常特别的涂鸦,开始出现在了纽约曼哈顿的墙壁上。刚开始就是些抖机灵的句子,"萨莫不会让实验室动物得上癌症,"而常见的是它们的落款都是萨莫。从1977到1980年,这些涂鸦持续了三年之久。最后在1980年,城市里各个角落都出现了一句话,"萨莫死了。"然后,这些句子不再出现了。有趣的是,现在我们知道,这些涂鸦不是某一个艺术家的作品,而是两个高中死党一起创作的,他们决定共用这个名字。
其中一个是艾尔o迪亚兹,在创作萨莫系列前,他玩了很多年涂鸦,很有名气,他与著名的美国作家诺曼梅勒联手,完成了一本关于涂鸦的书,而他的作品就出现在了那本书里,但萨莫系列没有出现他本人的落款,而是一个合称(萨莫)。但其中另一个人巴斯奎特,在当时鲜为人知。有趣的是,他们一同起步,有着同样的背景,一个人向另一个人学习艺术,毕竟其中一个人水平要高些。但几年后,巴斯奎特成为了作品最畅销的美国艺术家之一,几年前他的作品卖价达到了当代艺术家中的最高峰,高达1.1亿。
所以有趣的地方在于,这有点像我们在科学中常说的对照实验,比方说双胞胎对照实验。两个艺术家一起起步,玩着相同的艺术,结果几年后,就不再合作了,分道扬镳。其中的艾尔o迪亚兹现在还活着,但仍然处于纽约艺术圈的边缘,不是很出名,另一个却成为了最昂贵的艺术家之一。在当代的艺术家中是如此,究竟为什么两个同时起步的艺术家却有着如此不同的人生轨迹?上节课我们谈到了网络,我们谈到的很多事情都追溯到同一个问题,网络是什么形态的,它是如何出现的?我们已经开始了一项研究,我们想要研究网络如何帮助或影响个人的职业生涯。因为我们都处于多个关系网络中,无论是艺术家的社交网络,还是专业组织,或公司里的人脉,或是家族关系网络。
我们先是观察科学家,然后观察其他人,看社交网络如何影响个人事业。但我们很快意识到,试图探索科学家或任何一个人的职业轨迹,不仅关乎关系网络,还有很多别的因素关系到我们是否会成功。因此我们最终要开发一套工具和一套思维方法,来试图解答这个问题。
二、成功法则
法则一:成绩是个体的表现,而成功是群体的认知
今天我要说的是,如何看待成功,以及个人事业生涯中的成功。关于这个话题,我们首先要讨论的是两个很相似,却又截然不同的东西,那就是成绩和成功。当然成绩和个人相关,是我们所做的事情反映了我们在特定任务中的表现,就好像我们跑多快,论文写得有多好,画画得有多有趣之类的。但是我们这次的课,要区分个人成绩与成功,成绩关乎你个人,关乎你的行动,而成功关乎群体,成功反映了社会群体如何观察并承认和嘉奖你的表现。从这个角度说,重要的地方在于,个人成绩通常是很难衡量的,但现如今,成功的定义是以集体为单位的,也就是说有多个数据点。这意味着我们可以用大数据的方法,相对准确地衡量某个行业群体中间成功如何出现。在之前的课上,我试着归纳定律,那么今天的课里,第一条定律就是,你的成绩只和你自己相关。但你的成功则关乎群体,关乎群体如何看待。
法则二:成绩驱动成功
理解你的成绩,要注意的是,常把两种衡量标准混到一起。举个例子,德约科维奇,一个网球选手,我们讨论他时,会出现很多个角度的故事。可以讨论他有多出名,有多少人在谷歌上搜索他,还可以讨论他的世界排名,讨论他的得分,讨论他究竟赢了多少分,讨论他的输赢,讨论有多少人浏览他的维基主页,讨论他赚了多少钱,无论是通过打比赛还是代言。我们在讨论时,观点是混合多元的,把成绩与成功混在一起。我们讨论的那些事里,有的只和他自己相关,还有一些则关乎我们。我们来试着把它们分开,他的输赢、得分和排名,他赚的钱,都是我们所说的成绩的衡量标准,这都只和他个人赛场的表现有关。但是多少人在维基搜索他,多少人在谷歌和维基上浏览他的主页,他能接到多少代言,这些都是成功的衡量标准,因为这关乎群体如何看待他。我们尝试得出这么一个结论,就是成绩驱动成功。
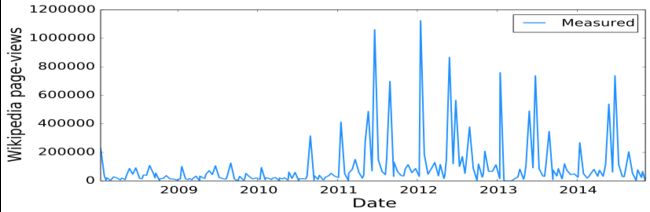
这有哪些衡量标准?你的行动、你的成绩,决定了群体给你的回馈。首先我们关注的是,如何准确衡量成绩。以网球为例,通常我们衡量成功的标准,是看有多少人浏览他的维基主页,这和那个人的成绩是紧密相关的,所以这种衡量还比较准确,大多数人都会用到。这些衡量方法,你或许没意识到科学家们可以研究维基主页背后的数据,看看有多少人在同时浏览一个页面。收集这些数据,继续观测这些指标,看每周会有多少人访问德约科维奇的维基主页,任何网页都可以这样去测量。如下图所示,在这个例子里我们可以看到,有一些清晰的访问峰值,都和他参加的比赛相关。你可以看到,2011年他的事业开始腾飞,那时候他赢得了许多重要赛事的大奖。
现在挑战在于,如何继续仅仅通过成绩来预测成功。仅仅通过成绩意思是,我们只关注和他的赛场成绩相关的信息,并利用那些信息,也就是利用他个人的成绩,来预测究竟会有多少人出于好奇,去浏览他的维基主页。为了做到这一点,我们最终创建了一个公式,如下图所示。这个公式的独特之处在于,右边的数据只和赛场上他的表现有关,左边则是预测多少人会好奇地浏览他的主页。我们主要说一下右侧的内容,但我想展示一下这个公式的准确性。下图红线反映的是,这个公式对于访问情况的预测。你可以看到,它对公众对德约科维奇好奇心的预测。
这是怎么做到的呢?因为这个预测的准确度来自事实,在网球这方面,成绩确实决定了成功,他的成绩决定了我们会有多好奇,可以说,右边的这些数据,比如锦标赛的含金量,就是这个比赛有多厉害。比赛数量,就是他之前打过的比赛数量,打了多少年比赛,对手的等级排名,他自己的等级排名,最顶尖的对手,他们的排名等等,这些都是和成绩相关的指标。一旦有了这些数据,我们就能准确,预测我们对他的好奇心,不仅仅是他,在专业的网球锦标赛中所有主要的男性选手,每个人预测和实际观察到的网页浏览量都大致一致,女性网球选手也是一样。这种一致性,这些点在45度角斜线周围分布的事实告诉我们,通过成绩,我们就可以预测成功。成绩决定了成功,或许你们并不惊讶,也不应该惊讶,这也是我们在学校里,反复学到的,不是吗?必须努力学习,努力工作,只有这样你才能成功,这也是我们教育系统的基础。
法则三:成绩有局限
现在要做的是,继续深入下去,看成绩和成功在其他群体上的反映。从表现开始,首先是我们可以精确衡量表现的领域,比如赛跑,赛跑有一维的成绩参数,那就是跑步速度,或者说跑步所花的时间。画面中显然是博尔特,地球上最快的人。因为他赢了这些比赛,没有人质疑他是最厉害的赛跑选手,有趣的是,当你看他的表现时,看奥运会上,他获胜冠军所花的时间,你会发现他的成绩和输掉的人相比,只好一个百分点甚至更少,输掉的人就变成了第二名。即便如此,赛跑中前两名之间的差异,实际上不到一个百分点。不仅如此,如果你真的比较我和博尔特,百米赛跑的速度,我当然跑得不快,但他的速度也比我快不了十倍,对吗?或许只是两倍吧,所以这里反映的是,成绩上确实不会存在太大的差异,对吗?世界顶尖的田径远动员,也只比我快两倍。这让我不禁思考,我们究竟如何准确区分顶尖与非顶尖的表现呢,尤其是比如里约运动会的游泳项目?不寻常的地方在于,匈牙利的游泳选手和另外两名选手共同获得了银牌,包括美国冠军菲尔普斯。
我为什么要分享这个例子呢,这是因为赛跑和游泳是为数不多的衡量标准独特,且精确的领域。我们发现,如果可以准确衡量个人表现,那么前几名选手之间的差距只有分毫,几乎是无法测量的。换句话说,我们发现,奔跑的速度是有限的,不管是游泳或是其他运动,我们做测量后,会发现同样的规律,那就是法则三:成绩是有局限的。有局限的意思是,最优者并不会比次优者的成绩高出一个数量级。顶尖选手之间只会有细微的差别,这不仅适用于体育,从商业到科学的其他领域,我们都可以衡量个人成绩,成绩最好的人之间,差异微乎其微。成绩是有限的,在顶尖范围内成绩是相当的。那么成功呢?
法则四:成功没有上限
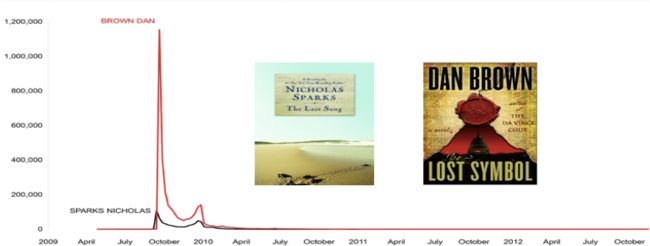
要理解成功,我们还是看一个参数。举个例子,几年前我的书在美国出版,我在纽约和我的出版商聊天,出于好奇,我们看了那个星期的热销第一是哪本书,那是2009年10月4日,就是看看要和谁竞争。最后发现第一是丹·布朗的《消失的符号》,第二是尼古拉斯·斯帕克的《最后一支歌》,当你看到最畅销的名单时,感觉他们的成绩很接近。我们甚至会想,如果尼古拉斯·斯帕克的团队再加把劲,他可以轻松超过丹·布朗。确实,哪本书更好是没有定论的。相较而言,还是会有人试图说服那些写书评的人,尼古拉斯·斯帕克的书比丹·布朗的更好。
那么,我们来看看成为畅销书背后的数字。我找到了一些数据,尼古拉斯·斯帕克那本书在那一周卖了多少本。这个数字很了不起,尼古拉斯·斯帕克的这本书卖了约十万本,这在美国市场是一个了不起的数字。我是什么意思呢,在美国,如果你想上纽约时报热销书榜,那么你每周要卖出大约三四千本,如果你的销量到了一万,那几乎可以肯定你就是第一了。然而,尼古拉斯·斯帕克那一周售出了十万本,远远超过当第一需要的销量,结果它却不是第一。为什么呢?因为丹·布朗的书也在周末出版了,那一周他卖出了两百万本。这个例子表明了,成功有一个非常重要的属性,成绩是有局限的,第一名只比第二名优秀一点点,但是成功的回报是无限制的差异,成功或不成功之间很容易达到一个数量级的差距。我的意思是说,成功是群体给予个人的,你到底能获得多大的成功是没有明显上限的。我们都可以在同一周内,购买同一本书。换句话说,这就是我所说的第四条定律,成功是没有上限的。
法则五:成功造就成功
我们整理一下,刚刚讨论的一切,我们说成绩决定成功,成绩是有局限的,而成功没有上限,问题是为什么会这样?成绩上只有一个百分点的差距,怎么最后的成功却有这么大的差距,达到一个数量级呢?而讨论这个机制,不需要想太多,这和我们在讨论网络时所说的相关,也就是偏好连接,也就是富者更富的机制。我们前面讨论过,在网络中我们发现,早期的节点,实际上是脱颖而出的,你已有的越多,新得到的就越多。丹·布朗卖的书越多,就有越多人讨论他的书,你就越有可能买他的书。一首歌越火,越多人讨论它,越多人会开始听它。从根本上说,成绩差异很小,而成功差异却很大的原因就在于,成绩难以区分的时候,富者更富的机制就会随机在网络中选择,并不一定基于成绩差异,选出一些枢纽。
现在你可能会问,我们如何开始这个进程,如何在自己身上开启偏好连接?在这个方面,我们有相当多的研究。我发现最好的例子,目前最好的一个实验,是由美国社会学家阿诺特·范德利特完成的。他问了个简单的问题,这些枢纽是否真的更好,是否比其他的成绩表现更好呢?能否产生一种自反馈的增强?是否有可能,枢纽是通过偏好连接产生的呢?问题是,如何做出正确的选择呢?如何从偏好连接机制中,辨别出最佳的成绩呢?所以,他决定做一个实验,实验是这样的。
他去维基百科,收集并选择了维基百科的千名最佳编辑,这些编辑都是维基的幕后人员,他们通常是志愿者。阿诺特·范德利特只是简单看看每个编辑的活跃程度,他们在不同页面上做了多少次不同的编辑,从最好的一千名编辑里,他最终随机选择了两百人。这些都是维基百科的最佳编辑,他们被随机分入一组和二组,他选择的一组和二组几乎没有什么差异。他给第一组成员每人一个奖励,也就是一颗五角星。每个人都可以奖赏维基编辑五角星,如果你在维基百科,很喜欢某些编辑的文章,你就可以给他们赠送五角星,任何人都可以这样。阿诺特·范德利特给了第一组一人一个五角星,却没给第二组。你要意识到,这与两位艺术家的故事有点类似,两个组没有太大差别,无论是表现还是行为,唯一的区别是,在某一时刻,第一组每个人都获得了奖励,第二组却没有。然后他只是在一旁观察,两组发生的事情。三个月后,网友开始给这些编辑奖励五角星。事实是,两组获得的奖励数不同。也就是说,第一组获得了大约十二颗星,第二组只获得了三颗,当然,这是统计上显著的差异。而实际上,这都是因为阿诺特·范德利特的实验,他给予编辑的早期奖励,导致他们获得更大的成功,他让他们显得更值得嘉奖。因此当其他人看到他们的编辑成果,他们会想,他已经得了星了,那我再给他一个,自然不会出错,毕竟他们已经是非常受尊敬的编辑了。然而在第二组中,没有先前的奖励,他们必须通过自己的行动来获得奖励。这就是一个例子,表明我们可以刺激偏好连接,这就是第五条定律。成功造就成功。这一点很关键,尤其是当我们无法区分顶尖群体的表现时,就好像我们无法区分维基编辑的表现,有限的成绩催生出无限的成功。一些人将被选中,并取得巨大成功。
法则六:任何时候都有可能成功
接下来的问题出现了,这种成功是什么时候出现的?在个人的职业生涯中,它何时出现?这就是我们要讨论的下一个话题。我尝试以自己的职业生涯来讨论这个话题。我是一名科学家,这意味着我的工作主要在于发表科研论文,研究界通过引用来承认,或不承认我的论文。是否有人阅读我的论文,或者觉得它很有趣,根据我的论文写他自己的,最后引用我的话,所以在科学中,论文成功的标准,就是引用次数。如下图所示,就是我的科研生涯,这里的每个圆圈都对应于我在整个职业生涯中发表的每一篇论文,直到大约五年前为止。垂直轴显示了,文章在十年内获得的引用次数,这都是有限的。你可以看到,我职业生涯的三个不同部分,我的职业生涯的前十年,真的很忙,但我没有得到很多认可,因为部分论文几乎没有任何引用,这就是我职业生涯的第一部分。然后在1999年,在一篇高影响的论文之后,我发布了又一篇影响度较高的论文,就是这个时候,我开始转变,从材料科学转向网络科学。这些都是我初期的网络科学的论文,可以看到,这些论文的影响力与我之前的论文完全不同,一篇好论文后,又是一篇大获好评的论文。如果要我形容当时的心情,大概如上图所示。就是这样,一切都很顺利。问题是,在此之后会发生什么?这方面的问题在于,没有足够的时间来研究这些论文是否会具有较高的影响力,因为我们需要等待十年来观察引用次数。我想知道,我的校长也想知道的是,这之后会如何?我会继续这一发展轨迹吗,还是说我会丧失战斗力?
那么让我们回答这个问题吧,我的职业生涯在哪里,我们对自己应该有什么期望。事实证明,在这个领域,有很多心理学研究来解决这个问题。特别是,心理学家的研究显示,你如何获得某种技能,无论是学习弹钢琴,还是成为商人,无论你的技能是什么,当你开始锻炼某种技能,你的表现会日益精进,然后你会在某个时刻达到最高峰,这或许要花上五年十年。那之后或许会有轻微退步,但很长一段时间内,你会持有这种技能,一旦你学会,你可能不会长期处于职业的顶峰,但你还是会很擅长这件事。因此当你仔细观察,你会发现,这很类似我的职业生涯,或许我的轨迹就会这样,但我还是想,定量分析之后的轨迹,我想知道规律在哪里。
为了达到这一目的,我不禁想这需要多少年我才能发布我最具影响力的论文。在这个案例中,是我职业生涯中的第63篇论文,在我学术生涯的第十三年,所以我们衡量的是学术年龄,而不是真实的年龄。因为我们并不总是知道,这个人是什么时候开始从业的,成果又是在什么时候产出的。而实际上我好奇的,不是我经历了什么,而是其他科学家都经历了什么,也是这一点,将这个演讲和其他的成功学演讲区分开。关注成功人士的文章,数不胜数,但从科学的角度来看,这是一个偏离样本,你或许会得出一个结论,那就是成功人士之所以成功,是因为他们六点起床,但是这里还有其他1000万的人,他们在六点钟起床的人,却并没有成功,这就是组合问题。在某种程度上,如果你想知道某种药物有效,你需要一组给对照剂,一组给以药物来验证它有效。这样看,我们设计研究的方式是我们不会只关注成功的科学家,我们关注所有的科学家,对每个人我们都测量了他们在职业生涯的哪个阶段,发表了最具影响力的论文。无论是荣获诺贝尔奖的发现,还是一个不那么起眼的发现,但是是在这个人所处的行业中比较重大的发现。
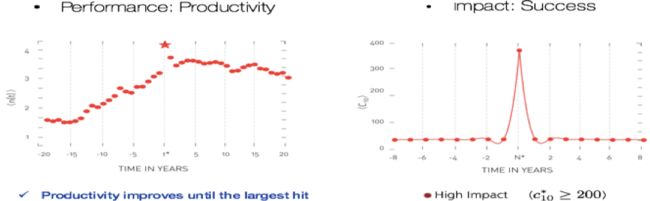
我们这样做的原因是,当我回顾我的职业生涯时,你可以看到这个趋势,之前有一些论文都是高影响力的,所以你可以看到一些变化。而且你可以看到,即使没过多久,在我达到这个里程碑后,我还能够制作出其他高影响力的论文。那么在多大程度上,你的职业生涯是可预测的呢?先看看个人成绩,如下图所示是成绩,每一个科学家最具影响力的论文会出现在中间。那么从成绩中,我们是否能看出他们即将实现职业上的突破呢?为了研究这一点,我们要观察他们发布的论文数量,也就是生产率,即关键的突破时刻,在靠近这个点的时候,他们的生产率实际上正在快速增长,然后它会停留在那里,可能会略微减少。所以某种程度上心理学家是对的,看生产率,你可以看到那一刻的到来,你可以看到有所持续。但这是生产率,而不是成功,这是成绩的一项衡量标准。
再来说成功。看看在最具影响力的论文之前和之后的论文影响力如何呢?我们的研究,从左上图可以看到峰值之前,生产率是一直增加的。那成功呢?右上图是一条曲线,在成功之前,曲线没有大起伏,之后也没有。这个结果很让人失望,因为这实际上是一个在营销学领域很出名的曲线,常被称为指形曲线,因为它告诉我们,我们无法预测成功,也不能从中学到什么。所以个人表现在职业生涯中是会一直变化的,但成功似乎是个人职业生涯中的突然出现的一个事件,难以预料。继续下去,看那一时刻何时到来,在职业生涯的何时呢?我们发现,在这个领域有很多研究,尤其是在天才研究方面,这些研究发现,通过观察表现卓越的人群往往是年轻人会有重大的研究发现,所以想突破,要够年轻。也正是因此,爱因斯坦曾经声称,"一个人在30岁之前,没有对科学做出巨大贡献的话,那他就永远做不到了。"他为什么这么说呢?他之所以这样说,是因为他观察他的同事,他为之工作的人,他的对手,从海森堡到费米狄拉克,再到维格纳,他发现,这些人中大多数都在三十多岁,在量子力学或物理学方面,做出了重大贡献,这里面很少有人能在岁数更大的时候得出成果。所以,在天才研究中有这样一个教条思想,就是年轻人才有创意,随着年龄的增长,创意会衰减。这不仅适用于科学,技术和商业等方面也一样。所以我们说,看我们是否能在科学家中同样发现这种规律,我们再次回顾如右上图所示的曲线,看人们在多大岁数,学术年龄多少的时候,得到最重大的成果呢。
如左下图所示,不仅是我,还有其他所有科学家的事业轨迹,而且你看,每条线对应一个科学家,红点对应时间,就是在学术生涯中,写出最具影响力论文的时候。无论这个论文是否真的具有很大的影响力,或者是影响力不太大,无论你的职业以什么衡量成功。你看下图,看不出任何规律,因为峰值无处不在。所以我们需要继续,应用一些大数据工具来找出答案。因此我们要问的是,在职业生涯的头两年或五年中,得到最重大的发现的概率是多少?这就是我们得到的曲线,这就是你的最具影响的论文,在前十年、二十年,或三十年内出现的可能性。事实上我们确实发现,和有关天才的研究类似,即便是非天才、普通的科学家,在他们职业生涯的早期,大约在职业生涯的十到十五年内,得到最重大的发现的可能性非常高,然后会不断降低。因此针对普通科学家的数据,证实了人们对天才的研究。
基于这些数据,我发现,我已经入行快三十年了,因此我完全应该处于职业生涯的末期阶段,因为我有不到百分之一的机会来获得比我之前的发现更重大的成果。所以基于此,我可以得出结论,我应该环游世界,四处宣传我的光辉往事,因为没有理由去继续探索了。但我才不承认了。然后,让我们看看数据背后的东西吧。为了理解这些数据模式,先要有一些参考框架。这里我们不妨假设这种趋势是随机的。如果人们在职业生涯中,发表影响力最大的论文的时间是随机的呢,这很容易检验。我们保留了每个人的职业信息,但我们打乱了他们的论文,发布论文的时间依旧保留,但把论文顺序打乱了,这样就是完全随机的了。这样的话,哪一篇论文影响力最大呢?我们就继续研究下去吧,看随机情况下结果如何。在随机的情况下,我们得到了与原始曲线相同的曲线,这非常令人费解。当我们仔细查看数据时,我们意识到,这只不过是生产率曲线,因为随机曲线只是表明,在你的职业生涯的某个阶段,你有多大可能性发表论文,所以通过这些数据图,我们发现事业早期阶段,生产率较高,之后会大幅递减。
如果综合起来看,我们会问,为什么这两条曲线是一样的?这反映出,创造力没有年龄依赖性,年龄只和生产率有关。让我更准确一点,回到如右上图所示的曲线,如果我只是观察每个科学家的职业生涯,不把他们的论文按时间顺序排列,我只是说第一、第二、第三、第四、第五直到最后一篇,然后每个科学家都如此处理,统一到相同尺度。那么两条曲线相同的事实表明,就论文而言,事业早期或晚期的概率都不高,这就是如下图所示展示的内容。我选取了每一位科学家的第一篇和最后一篇论文为对象,把数据全部铺开,用同一标准,无论是十年还是三十年,然后再看,你发表的前百分之十的论文中获得最大影响力的概率是多少,然后看前百分之二十等等,柱状图是基本水平的。所以这真的告诉我们,就你所做的项目来说,影响力最大的时机,是完全随机的。因此你所做的每一个项目,都有同样的机会获得最大影响力,但因为你年轻的时候,生产率很高,所以你更有可能有所突破,因为你更乐于尝试。或者换句话说,你知道,成功有点像买彩票,每个项目都是你购买的彩票,如果你在生命的前些年,使劲买彩票,并且之后停止购买彩票,那么显然你会发现,在你年轻的时候更有可能中奖。现在的数据明显表明,创新能力没有年龄方面的依赖性,也就是你不知道突破何时到来,概率都是相当的。
让我给你们看一些例子,看看弗兰克·维尔泽克的职业生涯,他获得了2004年诺贝尔物理学奖,而这个奖项来自他最开始写的一篇论文,是他研究生时期写的第一篇论文,结果四年后,他就因此获得了诺贝尔物理学奖。当然,这与年轻人能创新的理念是一致的。但再看约翰·芬恩,实际上也是一个很好的例子。约翰·芬恩,在2002年,因为他在被耶鲁大学强制退休后所做的一项研究,获得了诺贝尔化学奖。最近有一些很漂亮的数据,揭穿了一个说法,那就是在硅谷,年轻才意味着创新。
当然,大家都知道facebook的创始人,谷歌的创始人等等,他们成立公司时都很年轻,因此人们会觉得,如果你想在硅谷获得成功,你必须年轻。那么当你真正去看那些成功的公司,市值数十亿美元甚至更高的公司,以及创始人的年龄时,你会发现一个水平的分布,从二十出头到七十几,所以那不是真的。并不是只有年轻人才能创立数十亿价值的公司,只不过是我们更关注年轻人,因为这样的故事更精彩。我们喜欢写新闻,写书讲述他们的故事,我们往往忽略了和那些年轻人一同创立成功公司的中老年领袖。所以结论非常明确,成功和年龄无关,它随时可以到来,但关键在于保持生产率和持续尝试。实际上,成功率下降的原因,只不过是因为人们不再努力尝试了,年龄渐长后,他们不再去成立新公司了,他们不再去写论文,他们不再去写新小说等等,因此,他们成功的机会将大大减少。
法则七:Q-factor是成功的决定性因素
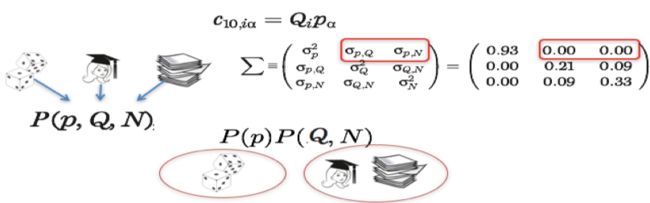
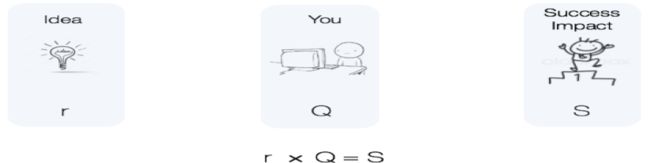
现在问题是,成功是随机的,这意味着什么?通常说来,这种随机性常被视为是不好的,但在科学家眼里,这是机遇。因为奇怪的是,我们常常认为如果某些东西是随机的,那它就是不可预测的,但恰恰相反,如果某些东西是随机的,那它背后的可预测性很强,因为你理解了背后的模式。事实证明,每次探索、每个项目成功几率都是相当的,也就是我们可以将事业建立在一个创新模式上。我们作为科学家,我们还在思考,看看如何把这个融入公式里。所以最后,我们开始观察他们如何启动一个新项目?先是有了一个灵感,但不知道它是否有价值,所以我就想说,这就相当于是个随机值。它有可能是个好主意,对应这个数值就会很大。如果是个不太好的想法,那数值就会很小。也就是如下图所示的p值,随机的,代表你一开始的想法。然后,你从这个想法开始,变出产品,或许是个公司,又或是论文、艺术作品,无论是什么。我们将想法变成产品的能力是各有不同的,经验不同、才干不同等等,所以如下图所示的Q值,表示你将想法付诸实际的能力。最后,是成功的衡量标准,衡量有多成功,或许是你公司赚的钱、员工数量、论文引用的次数等等。所以实际上我们想说的是,可以很轻松地展示创新的价值,也就是想法的价值,乘以你将想法付诸实际能力,会让你得到有关成功的答案值。
现在就科学家的案例而言,我们能够精确测量这些参数,我们发现了一些意外的结果。首先,你或许认为随着年龄的增长,随着你的经验积累,你会更懂得如何挑选新的灵感,所以你会知道这不是一个好主意,那就换个方向,因此这意味着,经验充足和经验不足的人,想法价值是不同的。此外,随着年龄的增长,你将创意转化为产品的能力也会提高,我认为我将想法付诸论文的能力,要比二十年前我刚开始做学术时高得多的多。但数据显示则不然,数据显示的是,所有的科学家都分享着相似的灵感库,我和年轻科学家之间没太大差别,但至于我们会挑选哪些灵感,机会是一致的。这样看,事实证明,如果这种分离发生了,我们就会发现,创新的发生是一个简单的过程,想法就是r值,这是个随机数。然后是你自己的知识,Q值,然后你可以获得成功或影响力,就是随机数乘以Q,得出你的成功值。这个模型很精确地解释了,科学家是如何发表一篇又一篇文章的,它还解释了,为什么优秀的科学家也会发表糟糕的论文,那是因为他们采纳了一些糟糕的主意。一个接一个,它还解释了科学突破如何发生。
现在我讲一下创新的例子,看看这个故事会如何开展。你们都知道现如今的创新领袖,被认为是史蒂夫·乔布斯,这个模型能否适用于他的职业生涯呢?我不确定有多少人听说过Newton电脑,那是史蒂夫·乔布斯关于手持设备最初的构想,一款掌上电脑,这是个很不错的创意,多亏了iPhone,我们能知道它,Newton概念很好,但是执行很差,它依赖手写输入,但是手写识别功能很差很差,所以人们就不爱用了,之后,即便做了很多营销,也无济于事。所以这就是一个很好的例子,好创意没能被好好执行,所以影响力平平。史蒂夫·乔布斯也有过执行很好,但想法很烂的时候,也就是我们说的G4 Cube,虽然设计得很好,但是它的理念真不算好。当然,还有好主意加上好执行,相当于中头彩了,结果就是iPhone。所以,可以看到Q值,如果你有内在的Q值,它可以包容你犯错,一个接一个,做一个有一个项目,如果你继续尝试,那你再遇上好点子的时候,终会实现大创新。
现在的问题是,Q值如何随着年龄变化,随着我们变得更有经验,它是否会增加,还是下降。在科学家的案例里,我们可以衡量这个值,只需要看他们发的论文就好,看影响力如何。令我们惊讶的是,我们发现,这里是低Q值的科学家、中Q值的科学家和高Q值的科学家,Q值的变化,它不依赖年龄。所以看起来 作为一名科学家,你刚毕业的时候,你带着当时的Q值开始工作,然后凭着这个Q值发表头几篇论文,整个职业生涯里这个值都不会有太大变化。如果你有高Q值,你也有可能写出很差的论文,或者做出很糟糕的项目,可能是因为你的随机数r没选好,但如果这个随机数r很大,你就有可能做出一个影响力很大的产品。但如果你的Q值很低,即便你的随机数r很大,也就是点子很好,你也执行不出来。这就是为什么我们发现这一点,那就是Q值在整个职业生涯中,并没有怎么改变。这对我们来说非常意外,因为我自己作为一名教育工作者,我希望结果结果是与之相反的。像上述简单的等式,很好地描述了个人事业中实现成功的模式。
可以看到,如果你知道你一个科学家的Q值,那针对他或她未来的事业,它就会是个很强烈的预测因素,有关Q值的有趣之处,它在个人生涯中,形成的时间很早,一旦我知道了这个值,就可以预测一个人得诺贝尔的机会有多大。可以发现,有些参数根本无法预测出某人是否会得奖,比如生产率,就是发表多少论文,根本无法预示你是否会获得诺贝尔奖。所以,不要试图通过高产能,来求取成功。但最具影响力的论文,是很好的预测因素。总引用次数或其他参数都无法预测,只有Q值能最好的预测,也就是一个人的能力值,这一点和他未来的发展是紧密相关的。因此,我们从这里学到的是,一个很简单的概念,如果你有高Q值,那么你不一定会很快成功,高Q值就像一个灌了铅的骰子,但想要投出6,你还是要一遍一遍扔骰子,所以如果你想把你的才能或能力转化为可衡量的成功,那你必须一直保持这个Q值。如果你的Q值很低,那可就不妙了,因为即使一个好主意,也不一定救得了你,因为你没足够的能力去实现它,做成好的产品。这样看,建议就是,尝试稍微地改变方向,转变到你有高Q值的领域上去。
我本人就是很好的例子。当我还是一名学生时,我想成为一名雕塑家,但我没有这方面的高Q值,这方面我很弱。尽管我做了诸多尝试,在工作室里一待几小时,上雕刻和绘画的课程,与此同时,我也在修物理课,我赢了一些物理比赛,潜意识之中我发现我的Q值,当时自然不会说Q值,在物理方面比艺术方面高得多。因此今天我作为一名物理学家,而不是一名雕塑家,站在你们面前。