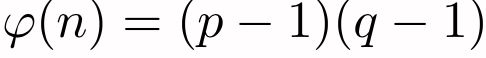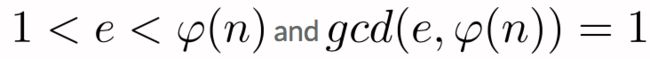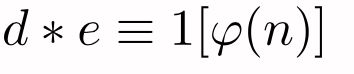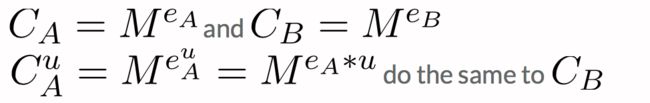Intro
很多CTF的crypto题目都有RSA题,而我每次看到RSA都很慌。。。因为数学差
在研究CSAW2018的Lowe时候看到一篇博客把RSA的原理和CTF中常用的一些攻击手段总结了一遍。这里我用中文转载一遍他的博客。
文章中的攻击都是针对CTF题的,所以有着很多的前提假设,在现实中很难碰到可以利用的情况。
RSA的原理
RSA是最经典的一个非对称加密算法。一个RSA算法有两个密码,公钥和私钥。公钥中包含着(n,e),私钥中包含着一些信息和(n,d)。
大数n是由两个素数相乘组成的:n=p*q
为了找到合适的公钥指数e,你需要首先计算n的欧拉函数:
注意:在真实的RSA运用中,我们不用欧拉函数而使用Carmichael’s totient function.
接着,我们要挑选e,e要满足一下两个条件:
也就是说e和phi(n)互质。
有了公钥指数e之后,你就可以计算得到私钥指数d。d是e对于phi(n)的摩反,也就是:
公钥和私钥都是以pem的格式储存,我们可以用python,openssl等方式解码公钥和私钥。
下面用python2来演示RSA加密和解密的过程:
首先是我们的公钥:
n = 30994968412821274638126108542140224647370292100079091608343041083209715023181825537637957453183815788151099869840363450721
e = 65537
我们将要加密的明文转换成数字形式:
>>> "My credit card number is 1337".encode('hex')
'4d79206372656469742063617264206e756d6265722069732031333337'
>>> m = 0x4d79206372656469742063617264206e756d6265722069732031333337
>>> m
2088672004503895363248317162088008321096572194316716175821104101929783L
然后计算c=m^e mod n来得到密文:
>>> c = pow(m,e,n)
>>> c
3740808283126743789473658216888004237756151970385422112230702175214670415045578511813428786937523016996521109011952458274L
接着利用私钥解密:
n = 30994968412821274638126108542140224647370292100079091608343041083209715023181825537637957453183815788151099869840363450721
d = 10949944362147351445695313961215384000802056441294706923101734114824865877971959648683318864984560110549528540371119079473
解密过程是计算m=c^d mod n:
>>> t = pow(c,d,n)
>>> t
2088672004503895363248317162088008321096572194316716175821104101929783L
>>> hex(t)
'0x4d79206372656469742063617264206e756d6265722069732031333337L'
>>> "4d79206372656469742063617264206e756d6265722069732031333337".decode('hex')
'My credit card number is 1337'
解析PEM文件
如果打开PEM文件可以看到的格式是这样的:
-----BEGIN PUBLIC KEY-----
MFwwDQYJKoZIhvcNAQEBBQADSwAwSAJBAIw/U51Fghh6WumZQjg9l3a6AjFZ+xm2
x2+9ja+8n8Yg95Hbxsp9vCpwlIol1A5wMo6p/hNlxzAE3/cY08eKzDMCAwEAAQ==
-----END PUBLIC KEY-----
-----BEGIN RSA PRIVATE KEY-----
MIIBOQIBAAJBAIw/U51Fghh6WumZQjg9l3a6AjFZ+xm2x2+9ja+8n8Yg95Hbxsp9
vCpwlIol1A5wMo6p/hNlxzAE3/cY08eKzDMCAwEAAQJAJearQxJYwSK31O9dDPPg
Le7AzvOBP4a8yP7R/o8cIp+3XdCXzuUreFzTWTXIg76tohg8cQb77HT/jVo2rLXa
AQIhAOrtFkJ0So2NZIp4xBPLqFozaSJNti8Yx8w1IOWoS2szAiEAmNQCPrBaB6p4
heIDYgaTYpJa4gbw3tLe82AAKzFLGwECIE/ZA37Uzd4s16ZlA6gCyZbW8H3zUd/S
GV6kFClauT+XAiBZuddbkNQ6vfYmvIw56Bxt+flLzMFsQSfOgaV3tmgfAQIgKW7C
LI1+rBn3TvmyLMZ7+3TEtVeTVRgabLWyOUjmv7w=
-----END RSA PRIVATE KEY-----
用python解析PEM的代码如下:
from Crypto.PublicKey import RSA
f = open('public.pem','r')
key = RSA.importKey(f.read())
print(key.n)
print(key.e)
也可以用openssl来解析:
openssl rsa -inform PEM -text -noout -pubin < pubkey.pem
破解方法1——因式分解大数n
RSA的安全性依赖于大数分解的困难。要知道私钥d就得知道phi(n),而phi(n)又等于(p-1)*(q-1)。
如果n小于256bits,我们可以利用brute force来得到p和q。一般n的最小大小是2048bits。
我们也可以利用数据库来查询已知的n:http://factordb.com
一旦知道了p,q我们就可以计算e对于phi(n)的摩反来得到d。gmpy2库中的invert()函数可以计算摩反。
破解2——共有大数n(加密相同明文)
如果有一种情况,每个用户有自己的公钥(n,ei)和私钥(n,di),他们有相同的n但是每个ei和di不同。他们加密了用一个明文M得到密文Ca,Cb。我们可以利用ea,eb和n来得到明文M。
对于他们的公钥指数ea和eb,它们两应该互质,根据Bézout’s identity我们可以知道存在u和v使得:ea*u+eb*v=1
已知ea,eb,我们可以计算得到u和v,从而利用Bézout’s identity可以得到明文M:
比如我们有公用的n:
n = 19085995833312192524007220630153244389942263922006889142154298425751808612835625879164268530070480609
两个人的公钥指数e1和e2,两个人的密文:
e1 = 31
e2 = 71
c1 = 6754157603566559210605055806173167464578011342930319568190139207096747909338872956835503565519657656L
c2 = 15442865769085690326152463737212582797117727243803209188030346754687972404658825954014788039636105165L
我们可以计算得到u=55 v=-24。因为v小于0,我们可以用c2的摩反的-v次方代替c2的v次方。
c2_inv = 12909978039651622455828981512398791612880793088232603583312672024505111979731377532780209633970663146
接着我们可以计算M=c1^u*c2_inv^-v来得到明文:
>>> M
101519529085530394070280463104338208011199968387105
>>> hex(M)
'0x45766520697320737079696e67206f6e2075732021L'
>>> "45766520697320737079696e67206f6e2075732021".decode('hex')
'Eve is spying on us !'
破解方法2——共用大数n(拥有一个n的密钥对)
上一个情景中我们需要共用大数的两个人加密同一段明文,我们可以得到明文的信息。这个攻击方法我们需要拥有一个和目标共享n的密钥对。对于RSA的e和d,我们知道它们满足e*d=1 mod phi(n),所以e*d-1是phi(n)的倍数。这个关系可以写成:(e*d-1)=k*phi(n)
因为phi(n)近似于n,所以我们通过计算k=(e*d-1)/n得到近似的k。然后通过phi(n)=(e*d-1)/k来得到phi(n)。拥有了phi(n),我们可以通过phi(n)除以对方的e来得到对方的d。示例如下:
已知的共享大数n:
n = 1249110767794010895540410194153
对方的公钥指数e:
e_CEO = 3
我们自己的密钥对:
e = 65537
d = 205119704640110252892051812353
计算k的近似值:
>>> k = ((e*d)-1)/n
>>> k
10761L
计算phi(n):
>>> phi = ((e*d)-1)/k
>>> phi
1249226845367429202098912705713L
检验phi(n)是否正确:
>>> phi*k == ((e*d)-1)
False
如果不正确则将k加一:
>>> k = k+1
>>> phi = ((e*d)-1)/k
>>> phi*k == ((e*d)-1)
True
得到phi(n)并且计算出d
>>> phi
1249110767793988630717933434880L
d_CEO = 832740511862659087145288956587
Decipher Oracle:
有时候我们会碰到一个解密服务,服务器可以解密任何密文但是唯独不能解密flag。这样我们就需要新构造出一个密文,通过解密那个密文我们可以得到flag。
假如flag的密文是c,我们可以加密得到一个密文c1=2^e mod n. 然后将c和c1相乘:C2=c*c1= M^e*2^e=2M^e.
将C2给server去解密:我们可以得到2M,将这个结果除以2就可以得到flag