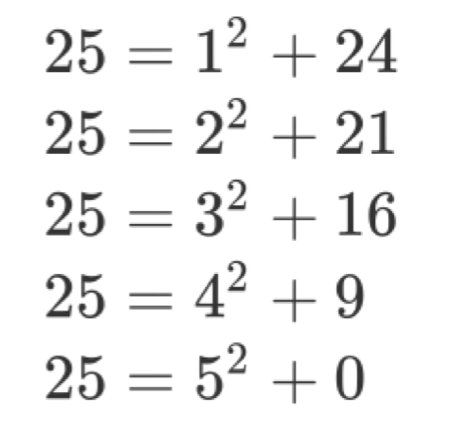首先我们来看 LeetCode 第 343 题,其实动态规划也包含了暴力求解,只不过我们按照一定规律,并且是在假设规模更小的问题已经得到解决的情况下,得到了我们原先要解决的那个规模的问题的解,我个人认为技巧在于“分类讨论”,而“分类讨论”的关键就在于“不重不漏”。
例题1:LeetCode 第 343 号问题:Integer Break
传送门:343. 整数拆分。
给定一个正整数 n,将其拆分为至少两个正整数的和,并使这些整数的乘积最大化。 返回你可以获得的最大乘积。
示例 1:
输入: 2 输出: 1 解释: 2 = 1 + 1, 1 × 1 = 1。示例 2:
输入: 10 输出: 36 解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。说明: 你可以假设 n 不小于 2 且不大于 58。
说明:同《剑指 Offer》第 14 题:剪绳子。
思路1:回溯,也可以理解为“暴力搜索”。遍历将一个数做分割的所有可能性,时间复杂度是 。
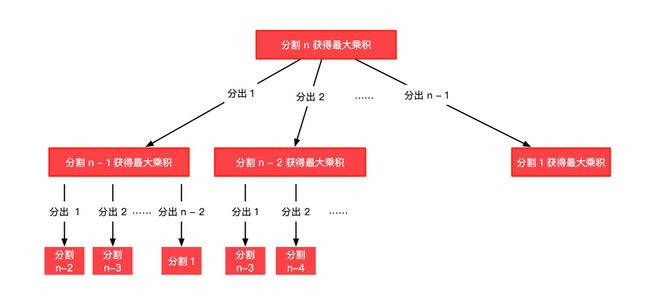
思路2:关键:“至少分割成两个部分”。分析这个问题的递归结构:“至少分割成两个正整数” = “一个正整数” + “另一个还没有分割的正整数”。这道题解题的关键在于“至少分割成两个正整数”,从这个角度出发,就能够得到我们“自顶向下”思考这个问题的路径,进而使用“记忆化搜索”或者“动态规划”得到原问题的解。
画出如下树形结构:
发现有大量重叠子问题。
定义状态: 表示正整数 经过分割以后得到的数字乘积的最大值。
则状态转移方程是:
从这个过程中体会:1、原问题的解是规模更小的子问题的解的组合;2、“状态”定义好了,上面的那个等式,其实就是“状态转移方程”。
对于每一个状态而言,还要再比较“不再继续分割”和“继续分割”,取当中的最大值。由上面的思路,我们可以写一个递归方法。
下面,我们给出 3 个解答,这 3 种方式的解答体现了我们思考“线性规划”问题的一般步骤。
Java 代码:不含记忆化搜索的递归
/**
* 没有记忆化搜索的递归解法
* 这个版本提交给 LeetCode 是通不过的
* Created by liwei on 17/10/3.
*/
public class Solution {
public int integerBreak(int n) {
int res = breakInteger(n);
return res;
}
/**
* 将 n 进行分割(至少分割成两个部分),可以获得乘积的最大值
* @param num
* @return 将 n 进行分割得到的乘积最大值
*/
private int breakInteger(int num) {
if (num == 1) {
return 1;
}
int res = 0; // 这个初始值可以设置为 0 吗,1 行不行?
for (int i = 1; i < num; i++) {
// 关键之处:状态转移方程,其中 i * (num - i) 这一步很关键,千万不能漏掉
// 这里有一个陷阱,就是不能忽略能不能继续分割的情况
res = max3(res, i * (num - i), i * breakInteger(num - i));
}
return res;
}
private int max3(int num1, int num2, int num3) {
int temp = Integer.max(num1, num2);
return Integer.max(temp, num3);
}
// 对于 2 和 3 这种分解之后乘积不超过自己的怎么办?
public static void main(String[] args) {
Solution solution = new Solution();
int max = solution.integerBreak(3);
System.out.println(max);
}
}
Java 代码:加入了记忆化搜索的递归
/**
* 加入了记忆化搜索的递归解法
* Created by liwei on 17/10/3.
*/
public class Solution2 {
private int[] memory;
public int integerBreak(int n) {
assert n >= 2;
memory = new int[n + 1];
memory[0] = 0;
memory[1] = 1;
for (int i = 2; i < n + 1; i++) {
memory[i] = -1;
}
int res = breakInteger(n);
return res;
}
// 将 n 进行分割得到的乘积最大值
private int breakInteger(int num) {
if (num == 1) {
return 1;
}
if (memory[num] == -1) {
int res = 0; // 这个初始值可以设置为 0 吗,1 行不行?
for (int i = 1; i < num; i++) {
// 关键之处:状态转移方程,其中 i * (num - i) 这一步很关键,千万不能漏掉
res = max3(res, i * (num - i), i * breakInteger(num - i));
}
memory[num] = res;
}
return memory[num];
}
private int max3(int num1, int num2, int num3) {
int temp = Integer.max(num1, num2);
return Integer.max(temp, num3);
}
public static void main(String[] args) {
Solution2 solution = new Solution2();
int max = solution.integerBreak(9);
System.out.println(max);
}
}
Python 代码:动态规划,注意:将 进行分解的时候,以 为例: 与 是一个解, 与 的分解的结果也是一个解。
class Solution:
def integerBreak(self, n):
"""
:type n: int
:rtype: int
"""
product = [0] * (n + 1)
product[1] = 1
for i in range(2, n + 1):
product_max = 0
for j in range(1, i):
product_max = max(j * product[i - j], product_max, j * (i - j))
product[i] = product_max
return product[n]
Java 代码:
/**
* 动态规划的解法
* Created by liwei on 17/10/3.
*/
public class Solution3 {
private int[] memory;
public int integerBreak(int n) {
memory = new int[n + 1];
memory[0] = 0;
memory[1] = 1;
for (int i = 2; i <= n; i++) {
int maxValue = -1;
for (int j = 1; j <= i - 1; j++) {
maxValue = max3(maxValue, j * (i - j), j * memory[i - j]);
}
memory[i] = maxValue;
}
return memory[n];
}
private int max3(int num1, int num2, int num3) {
int temp = Integer.max(num1, num2);
return Integer.max(temp, num3);
}
public static void main(String[] args) {
Solution3 solution = new Solution3();
int max = solution.integerBreak(9);
System.out.println(max);
}
}
总结:先研究递归解构,再记忆化搜索,最后实现使用“动态规划”。即先“自顶向下”思考,再“自底向上”实现。
思路3:贪心。这个规律要写到 左右才能看清楚。
Python 代码:贪心算法:1、能拆出 3 ,就尽量拆出 3;2、最多拆出 2 个 2。
最优子结构
下面我们引入一个新的概念:最优子结构。
什么是“最优子结构”?
我们通过求解子问题得到的最优解,组成了我们规模更大的原问题的最优解,这样的动态规划问题,我们称之为具有“最优子结构”。
动态规划问题通常应用的场景是:我们直接求解这个问题感觉难度较大,但是我们把这个问题拆分为规模更小的问题的时候,这个问题的解通常也就能够找到,这样的解决问题的实现通常都要借助递归来实现。
下面完成一些练习,重点体会什么是“最优子结构”。
练习
练习1:LeetCode 第 279 题:完全平方数
传送门:279. 完全平方数。
给定正整数 n,找到若干个完全平方数(比如
1, 4, 9, 16, ...)使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。示例 1:
输入: n = 12 输出: 3 解释: 12 = 4 + 4 + 4.示例 2:
输入: n = 13 输出: 2 解释: 13 = 4 + 9.
分析:这个问题的关键就在于“拆”,既然可以“拆”成多个的情况,那么最基本的情况就是“拆”成两个,这两个中,有一个是“干净”的完全平方数,还有一个是没有被“拆”干净的数(对于小的数我们人可以一眼看出,计算机看不出),所以还要继续“拆”。所以递归结构是这样的:
例如:如果自己是完全平方数,就返回 。否则就是如下所有情况的最小值,我们以 为例进行说明:
得到的解为 ,其实就是 第 2 行和第 3 行的情况。
再以 为例:
得到的解也为 ,看第 行就知道了。
特别注意:剩余的那个数如果等于 是完全可以的。我们定义这个问题中 和小于 的时候,解全部为 。这一点也是非常合理的,因为小于等于 的数,都不能表示成“正整数”的完全平方数的和。此时当前考虑的这个数,就一定是完全平方数,直接返回 就可以了。例如:
Java 代码:
代码实现要注意的地方:
1、因为大的值要依赖小的值,所以求解 会依赖比它小的值,这是设立外层循环的原因;
2、内层循环的终止条件是 i - j * j >= 0,体会这里 = 0 是为什么;
3、既然是求最小值,默认值就应该是一个很大的值,但其实,最大的值不会超过 。
注意到,结果最多是 4。
Java 代码:
import java.util.Arrays;
// 与 Solution2 是同一种写法
public class Solution3 {
public int numSquares(int n) {
int[] dp = new int[n + 1];
Arrays.fill(dp, 4);
dp[0] = 0;
for (int i = 1; i <= n; i++) {
for (int j = 1; i - j * j >= 0; j++) {
dp[i] = Math.min(dp[i], 1 + dp[i - j * j]);
}
}
return dp[n];
}
public static void main(String[] args) {
Solution3 solution3 = new Solution3();
int numSquares = solution3.numSquares(12);
System.out.println(numSquares);
}
}
还可以使用广度优先遍历完成:
下面这篇文章中的动画清晰地展示了使用“广度优先遍历”的方法。传送门:图解LeetCode第 279 号问题: 完全平方数。
注意:BFS 在图论中建模的模板写法。
1、使用队列;
2、使用一个数组,表示是否访问过。
Python 代码:使用图的广度优先遍历
class Solution:
def numSquares(self, n):
"""
:type n: int
:rtype: int
"""
marked = [False for _ in range(n)]
queue = [(0, n)]
while queue:
level, top = queue.pop(0)
level += 1
start = 1
while True:
residue = top - start * start
if residue == 0:
return level
elif residue < 0:
break
else:
# 注意这里,如果访问过,路径肯定更长
# 所以只考虑没有访问过的情况
if not marked[residue]:
queue.append((level, residue))
marked[residue] = True
start += 1
Java 代码:
import java.util.LinkedList;
// https://leetcode-cn.com/problems/perfect-squares/description/
// 广度优先遍历
public class Solution {
// 使用 BFS 来解决这个问题
public int numSquares(int n) {
assert n > 0;
boolean[] visited = new boolean[n + 1];
LinkedList queue = new LinkedList<>();
queue.addLast(new Integer[]{n, 0});
visited[n] = true;
int curNum;
int curStep;
while (!queue.isEmpty()) {
Integer[] pair = queue.removeFirst();
curNum = pair[0];
curStep = pair[1];
curStep++;
for (int i = 1; ; i++) {
int next = curNum - i * i;
if (next < 0) {
break;
}
if (!visited[next]) {
if (next == 0) {
return curStep;
}
queue.addLast(new Integer[]{next, curStep});
// 只要添加到队列中,说明我们已经考虑过,就没有必要再添加到队列中
visited[next] = true;
}
}
}
// 正常情况下是不会走到这句的
throw new IllegalArgumentException("参数错误");
}
public static void main(String[] args) {
int n = 7168;
Solution s = new Solution();
int numSquares = s.numSquares(n);
System.out.println(numSquares);
}
}
练习2:LeetCode 第 91 题:解码方法
传送门:解码方法。
要求:一条包含字母
A-Z的消息通过以下方式进行了编码:'A' -> 1 'B' -> 2 ... 'Z' -> 26给定一个只包含数字的非空字符串,请计算解码方法的总数。
示例 1:
输入: "12" 输出: 2 解释: 它可以解码为 "AB"(1 2)或者 "L"(12)。示例 2:
输入: "226" 输出: 3 解释: 它可以解码为 "BZ" (2 26), "VF" (22 6), 或者 "BBF" (2 2 6) 。
思路:拿具体的例子分析,比如:。假设我们已经解决了 dp[0] 和 dp[1] ,从 dp[2] 开始考虑,分析 num[2]:
1、如果 num[2] 不等于 ,那么 dp[2] 的情况和 dp[1] 是一样的,完成编码,这是一种情况;
2、如果 num[2] 跟前面的 num[1] 合起来能够组成一个字母,那么 dp[2] 和 dp[0] 是一样的,完成编码,这是一种情况。
两种情况都能完成编码,求总数,其实就是他们的和,这里其实是加法计数原理的应用。
Python 代码:
class Solution:
def numDecodings(self, s):
"""
:type s: str
:rtype: int
"""
l = len(s)
if l == 0:
return 0
if l == 1:
return 1 if s[0] != '0' else 0
dp = [0 for _ in range(l)]
dp[0] = 1 if s[0] != '0' else 0
for i in range(1, l):
if s[i] != '0':
# 如果不是 '0' ,那么 s[i] 就可以编码,所以 cur 就至少是 dp[i-1]
dp[i] += dp[i - 1]
if 9 < int(s[i - 1:i + 1]) < 27:
# 可以和前面的数字组成一个编码
# 这个判断是在写出 dp[i] += dp[i - 2] 以后,看出数组下标会越界,而增加的讨论
if i - 2 < 0:
# 12
dp[i] += 1
else:
dp[i] += dp[i - 2]
return dp[l - 1]
Python 代码:
class Solution:
def numDecodings(self, s):
"""
:type s: str
:rtype: int
"""
l = len(s)
if l == 0:
return 0
dp = [1] + [0] * l
if s[0] == '0':
dp[1] = 0
else:
dp[1] = 1
for i in range(1, l):
if s[i] != '0':
dp[i + 1] += dp[i]
if s[i - 1] != '0' and int(s[i - 1:i + 1]) < 27:
dp[i + 1] += dp[i - 1]
return dp[-1]
说明:上面这段代码 dp[0] = 1 是故意这么定义的,为了防止像上一版代码那样的讨论。
记忆化递归的写法,我没有写好:
http://songhuiming.github.io/pages/2018/03/11/leetcode-91-decode-ways/
http://songhuiming.github.io/pages/2018/03/11/leetcode-91-decode-ways/
http://songhuiming.github.io/pages/2018/03/11/leetcode-91-decode-ways/
花花酱:这位哥们录制了所有 LeetCode 解法的视频和解题报告。
http://zxi.mytechroad.com/blog/dynamic-programming/leetcode-91-decode-ways/
Java 解法,看起来很简洁:
https://www.jianshu.com/p/edd9da18eb01
练习3:LeetCode 第 62 题:不同路径
传送门:英文网址:62. Unique Paths ,中文网址:62. 不同路径 。
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。
问总共有多少条不同的路径?
例如,上图是一个7 x 3 的网格。有多少可能的路径?
说明:m 和 n 的值均不超过 100。
示例 1:
输入: m = 3, n = 2 输出: 3 解释: 从左上角开始,总共有 3 条路径可以到达右下角。 1. 向右 -> 向右 -> 向下 2. 向右 -> 向下 -> 向右 3. 向下 -> 向右 -> 向右示例 2:
输入: m = 7, n = 3 输出: 28
思路1:机器人一定会走 步,即从 中挑出 步向下走即可,即 为所求。
Python 代码:
class Solution(object):
def __factorial(self, n):
res = 1
while n > 1:
res *= n
n -= 1
return res
def __combination(self, m, n):
"""
从 n 个物品里选出 m 个物品的组合数
:param m:
:param n:
:return:
"""
return self.__factorial(n) // (self.__factorial(m) * self.__factorial(n - m))
def uniquePaths(self, m, n):
"""
:type m: int
:type n: int
:rtype: int
"""
return self.__combination(m - 1, m + n - 2)
if __name__ == '__main__':
m = 7
n = 3
solution = Solution()
result = solution.uniquePaths(m, n)
print(result)
思路2:特别注意到其实在左边第一行和上边第一行,肯定都为 ,还有就是新一行的值只与上一行有关,所以我们完全可以只设置一维数组,将这道题完成。其实使用 个变量也可以完成。
Python 代码1:记忆化搜索,
class Solution:
def __init__(self):
self.cached = None
def __path(self, i, j):
if self.cached[i][j] != 0:
return self.cached[i][j]
if i == 0 and j == 0:
return 1
path_ways = 0
if i == 0:
path_ways = self.__path(0, j - 1)
elif j == 0:
path_ways = self.__path(i - 1, 0)
else:
path_ways = self.__path(i, j - 1) + self.__path(i - 1, j)
self.cached[i][j] = path_ways
return path_ways
def uniquePaths(self, m, n):
"""
:type m: int
:type n: int
:rtype: int
"""
self.cached = [[0 for _ in range(n)] for _ in range(m)]
return self.__path(m - 1, n - 1)
用测试用例得到的缓存数组:[[0, 1, 1, 1], [1, 2, 3, 4], [1, 3, 6, 10], [1, 4, 10, 20], [1, 5, 15, 35]]。
Python 代码:动态规划
class Solution:
def uniquePaths(self, m, n):
"""
:type m: int
:type n: int
:rtype: int
"""
dp = [[0 for _ in range(n)] for _ in range(m)]
dp[0][0] = 1
for i in range(m):
for j in range(n):
if i == 0:
if j == 0:
continue
dp[0][j] = dp[0][j - 1]
elif j == 0:
dp[i][0] = dp[i - 1][0]
else:
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
return dp[- 1][- 1]
动态规划得到的 dp 数组:[[1, 1, 1, 1], [1, 2, 3, 4], [1, 3, 6, 10], [1, 4, 10, 20], [1, 5, 15, 35]]。下面介绍更节省空间的一种解法:
我是如何想到的:把缓存数组抄一遍,或者自己把矩阵画出来,就能知道这个数组怎么来的。每一行,只依赖上一行的结果,我们完全可以用一行来逐步更新。第 1 个元素肯定是 1,并且第 1 行元素肯定全是 1。有点“背包问题”的意思:节约了空间。
Python 代码:
class Solution(object):
def uniquePaths(self, m, n):
"""
:type m: int
:type n: int
:rtype: int
"""
if m == 0:
return 0
dp = [1] * n
for row in range(m - 1):
for col in range(1, n):
dp[col] += dp[col - 1]
return dp[-1]
Python 代码:与上一版等价
class Solution:
def uniquePaths(self, m, n):
"""
:type m: int
:type n: int
:rtype: int
"""
dp = [1] * n
for i in range(1, m):
for i in range(1, n): # 从索引 2 开始走就行了
dp[i] = dp[i] + dp[i - 1]
return dp[-1]
练习4:LeetCode 第 63 题:不同路径 II
传送门:英文网址:63. Unique Paths II ,中文网址:63. 不同路径 II 。
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
网格中的障碍物和空位置分别用
1和0来表示。说明:m 和 n 的值均不超过 100。
示例 1:
输入: [ [0,0,0], [0,1,0], [0,0,0] ] 输出: 2 解释: 3x3 网格的正中间有一个障碍物。 从左上角到右下角一共有 2 条不同的路径: 1. 向右 -> 向右 -> 向下 -> 向下 2. 向下 -> 向下 -> 向右 -> 向右
Python 代码:
class Solution(object):
def uniquePathsWithObstacles(self, obstacleGrid):
"""
:type obstacleGrid: List[List[int]]
:rtype: int
"""
m = len(obstacleGrid)
if m == 0:
return 0
n = len(obstacleGrid[0])
if obstacleGrid[0][0] == 1:
return 0
dp = [0] * n
# 这一步不要忘记了
dp[0] = 1
# 再写后面几行
for row in range(m):
for col in range(n):
# 【就分下面这两种情况就可以了】
if obstacleGrid[row][col] == 1:
dp[col] = 0
elif col > 0:
dp[col] += dp[col - 1]
else:
# 第 0 列不是 0 就是 1
# 0 的情况首先判断了
# 什么都不做
pass
return dp[-1]
Python 代码:与上一版等价的写法
class Solution:
def uniquePathsWithObstacles(self, obstacleGrid):
"""
:type obstacleGrid: List[List[int]]
:rtype: int
"""
m = len(obstacleGrid)
if m == 0:
return 0
n = len(obstacleGrid[0])
dp = [[0 for _ in range(n)] for _ in range(m)]
if obstacleGrid[0][0] == 1:
return 0
else:
dp[0][0] = 1
for i in range(m):
for j in range(n):
if obstacleGrid[i][j] == 1:
dp[i][j] = 0
continue
if i == 0:
if j == 0:
continue
dp[0][j] = dp[0][j - 1]
elif j == 0:
dp[i][0] = dp[i - 1][0]
else:
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
return dp[-1][-1]
(本节完)