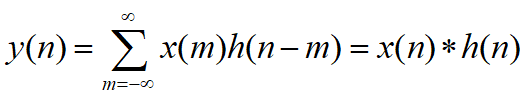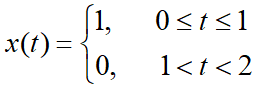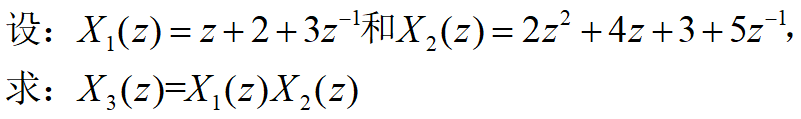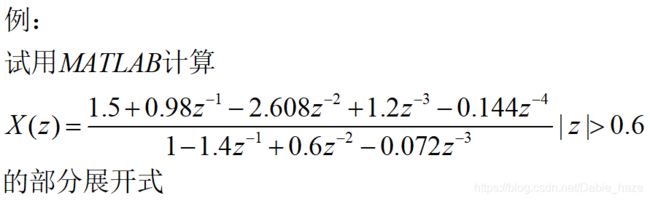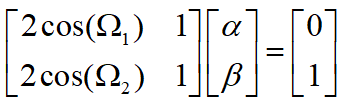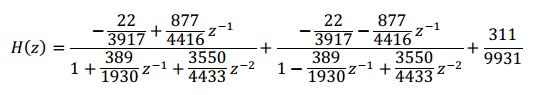数字信号处理：MATLAB实验代码整理

写在前面：本文中所有的matlab代码已整理，见下载资源“DSP_matlab.zip”。

1 常用的离散时间信号（DSP1_DiscreteTimeSignals.m）

1）单位样本序列

n1 = -2; n2 = 5;
n0 = 1;
n = [n1:n2];     % n1和n2是序列n的上下界
x = [(n-n0)==0]; % 给处置序列[]，只有当(n-n0)==0时值才为1
stem(n,x);       % 自变量写前面

2）单位阶跃序列

n1 = -2; n2 = 5;
n0 = 1;
n = [n1:n2];
x = [(n-n0)>=0]; % 只有当(n-n0)>=0时值才为1
stem(n,x);

3）实指数序列

% 实现x(n) = a^n
n = [0:10];
x = (0.9).^n; % 在含有数组的乘、除、乘方运算时需要点乘，表示对应运算
stem(n,x);

4）复指数序列

% 实现x(n) = e^((a+bj)*n)
a = 2; b = 3; % a表示实部，b表示虚部
n = 1:10;
x = exp((a+b*j)*n);
% 取实部，幅度谱
figure(1); stem(n,real(x));
% 取虚部，幅度谱
figure(2); stem(n,imag(x));
% 计算总幅度，画出幅度谱
AmpX = sqrt(real(x).^2 + imag(x).^2); % 计算总幅度方法一
AmpX = abs(x); % 计算总幅度方法二
figure(3); stem(n,AmpX);
% 计算相位，画出相位谱
AngleX = angle(x);
figure(4); stem(n,AngleX);

5）正弦序列

A1 = 3; w1 = 0.1*pi; b1 = pi/3;
A2 = 2; w2 = 0.5*pi; b2 = 0;
n = [0:10];
x = A1*cos(w1*n+b1) + A2*sin(w2*n+b2);
stem(n,x);

6）随机序列

N = 10;
x = randn(1,N); % 注意中间是逗号，第一个参数必须是1，表示在[1:N]产生标准正态分布随机序列
stem(x); % 不用输入自变量n

2 序列运算（DSP2_SequenceOperation.m）

1）信号相加

function[y,n] = sigadd(x1,n1,x2,n2)
% 两个序列分别为x1和x2，对应的自变量为n1和n2
% 运算结果为y，对应的自变量为n
n = min( min(n1),min(n2) ):max( max(n1),max(n2) );% 输出自变量取输入中最小和最大的
% y1和y2是将输入序列x1和x2的自变量范围扩大到n，因变量不变
y1 = zeros(1,length(n)); % 1×length(n)的矩阵，即一维数组
y2 = y1;
y1( find((n>=min(n1)) & (n<=max(n1))) )=x1; % 找出所有n中对应n1的自变量（返回一个数组），将因变量x1赋值给y1
y2( find((n>=min(n2)) & (n<=max(n2))) )=x2; % 找出所有n中对应n2的自变量（返回一个数组），将因变量x2赋值给y2
y = y1 + y2; % 对于自变量相同的两个序列，可以直接相加
end

2）信号相乘

function [y,n] = sigmul(x1,n1,x2,n2)
% 两个序列分别为x1和x2，对应的自变量为n1和n2
% 运算结果为y，对应的自变量为n
n = min(min(n1),min(n2)):max(max(n1),max(n2));
y1 = zeros(1,length(n));
y2 = y1;
y1( find( (n>=min(n1)) & (n<=max(n1)) ) )=x1;
y2( find( (n>=min(n2)) & (n<=max(n2)) ) )=x2;
y = y1.*y2; % 对于自闭那辆相同的两个序列，可以直接相乘，注意矩阵和矩阵的对应相乘，要用点乘.
end

3）信号加权

x1 = [1,2,3,4,5,6];
a = 3;
x2 = a*x1; % 直接乘以系数，如果系数是常数不用点乘
stem(x2);

4）信号移位

n = [1:10];
x1 = n;
stem(n,x1(n));title('x(n)')
n0 = 2; % 移位的大小
n2 = n-n0; % 相当于把自变量左移n0，由于作图时是把自变量和因变量数组对齐的，所以自变量左移相当于把信号左移 
stem(n,x2);title('x(n-n0)') % 整个信号左移，移位的结果是x(n+n0)：左加右减

5）信号反转

function[y,n] = sigfold(x,n)
% 输入序列为x，自变量为n；输出序列为y，自变量为n
% 注意反褶的结果只是对n进行反褶：若原信号是x(n-5)，反褶的结果是x(-n-5)，不是x(-n+5)
y = fliplr(x); % fliplr将矩阵沿y轴反褶
n = -fliplr(n); % 注意反转时n要取相反数
end

6）信号卷积

function [ y,ny ] = conv_m( x,nx,h,nh )
% 计算两个离散信号x和h的卷积，对应的自变量是nx和nh
% 输出卷积结果为y，对应的自变量为ny
nyb = nx(1) + nh(1); % 卷积结果的自变量最小值为输入序列自变量最小值之和
nye = nx(length(x))+nh(length(h)); % 卷积结果地自变量最大值为输入序列自变量最大值之和
ny = [nyb:nye]; % 确定上下界，得到卷积结果的自变量
y = conv(x,h); % 用conv函数直接计算x和h的卷积（不看自变量）
end

7）实验一_1：对信号进行加权、平移、反褶等基本运算操作

x = [1,2,3,4,5,6,7,6,5,4,3,2,1];% 原信号序列
n = [-1:11];
%% 画出原信号
subplot(2,2,1)
stem(n,x,'r-');title('x(n)'); % 首先画出原信号x(n)
%% 计算0.2*x(5-n)
x1 = 0.2*x; % 首先对信号进行加权，得到0.2*x(n)
n1 = n - 5; %  然后对信号进行平移，要得到0.2*x(n+5)，信号应该左移5，所以自变量-5
x1 = fliplr(x1);  % 最后对信号进行反褶。注意反褶只对自变量操作，得到0.2*x(-n+5)
n1 = -fliplr(n1);
subplot(2,2,2)
stem(n1,x1,'b-');title('0.2*x(5-n)');
%% 计算0.3*x(n-3)
x2 = 0.3*x; % 先加权，得到0.2*x(n)
n2 = n+3; % 然后平移，要得到0.3*x(n-3)，左加右减，信号应该右移3，所以自变量要+3
subplot(2,2,3)
stem(n2,x2,'g-');title('0.3*x(n-3)');
%% 计算y(n) = 0.2x(5-n) + 0.3x(n)x(n-3)
% y = 0.2.*x1 + 0.3.*x*x2;
[y1,m1] = sigmul(x,n,x2,n2); % 先得到0.3x(n)x(n-3)
[y,n] = sigadd(x1,n1,y1,m1); % 再把两个加起来，得到y(n)
subplot(2,2,4)
stem(n,y);title('y(n)');

8）实验一_2（主要看自编卷积的过程）：

卷积原理：

%% 自己求卷积过程
% 先求卷积结果ny
nx = n(1):n(length(n)); % x的自变量向量nx
nh = n(1):n(length(n)); % h的自变量向量nh
nyb = nx(1) + nh(1);
nye = nx(length(nx))+nh(length(nh));
ny = [nyb:nye];% 卷积结果y的自变量向量ny
 
% 再求卷积结果的因变量取值y
% 根据卷积原理，这里用k代替公式中的输出y的自变量n,用m代表输入x的自变量m，用t代表输入h的自变量n-m
% 其中index_k,index_m,index_t分别是自变量向量k,m,t的下标索引
for k = ny(1):ny(length(ny))   % k是输出信号y的自变量ny的值遍历
    index_k = k - nyb +1; % 值k对应自变量向量ny中的下标索引
    y(index_k) = 0; % 之后要累加，这里先初始化为0
    for m = nx(1):nx(length(nx))  % m是输入信号x的自变量nx的值的遍历
        index_m = m - nx(1) + 1; % 值m对应向量nx中的下标索引
        t = k - m;   % 对应公式中的n-m，是输入信号h的自变量nh的值的遍历
        if t>=nh(1) && t<=nh(length(nh))  % 判断t = k-m是否越界（是否在h的自变量的值nh范围内）
            index_t = t - nh(1) + 1; % 值t对应向量nh的下标索引
            y(index_k) = x(index_m)*h(index_t) + y(index_k); % 通过下标索引找到x(m)*h(t)，用迭代实现累加
        end
    end
end
y   % 求出的卷积结果是y，对应的自变量是ny

3 连续时间信号（见DSP3_ContinuousTimeSignalsSpectrumAnalysis.m）

1）周期信号傅里叶级数（以周期方波信号的求解为例）

% 信号在时域上是周期连续的，傅里叶级数在频域上是离散周期的
% 先画出周期方波信号
T = 2;  % 周期为T
dt = 0.00001;
t = -2:dt:2;  % 为了模拟时间上的连续，引入很小的变化值dt（如果没有dt，t只有5个值，是离散的） 
x = u(t) - u(t-1-dt); % 在0和1之间是高电平，x只是一个周期内的方波信号，为后面的傅里叶级数求解做准备。注意这里要-dt！！不然相位谱会有负值
subplot(2,2,1);plot(t,x);  % 画出一个周期内的效果x，连续信号作图用plot
x1 = 0; % x1是周期性的方波。注意要记得赋初值0
for m = -1:1    % 周期延拓
    x1 = x1 + u(t-m*T) - u(t-1-m*T-dt); % 在m*T和m*T+1是高电平。注意要把x1加上去，不然是覆盖。同样要-dt
end
subplot(2,2,2);plot(t,x1)   % 画出多个周期的效果x1
 
% 求周期信号的傅里叶级数
w0 = 2*pi/T;   % 根据周期计算角频率
N = 10;        % 谐波次数
for k = -N:N   % 画出正负对称频谱，k即频域上频点的取值
   ak(N+1+k) = (1/T)*x*exp(-j*k*w0*t')*dt; 
   % t'相当于进行了求和运算：x是1×length(x)的矩阵，t'是length(x)×1的矩阵
    % dt相当于把积分区域分成了许多个小的长方形进行离散求解
   % 注意这里x是一个周期内的（傅里叶级数的计算公式中是对一个周期求解），不能用x1 
   % ak是谐波的权重，当谐波个数N足够大时，就可以近似地表示x(t)
end
subplot(2,2,3);stem([-N:N],abs(ak)); % 画出幅度谱，离散频谱用stem
phi = angle(ak);   % 计算相位phi
subplot(2,2,4);stem([-N:N],phi);     % 画出相位谱，离散频谱用stem

2）非周期信号的傅里叶级数（以一个[-2,2]上的分段函数为例）

% 非周期连续信号的傅里叶变换（频域上）是连续周期的
dt = 0.01; % 为了模拟连续时间，引入dt
dw = 0.1;  % 为了模拟连续频谱，引入dw
t = -10:dt:10;
w = -4*pi:dw:4*pi;
% 分段函数
y1 = t+2;  % 当-2<=t & t<-1时
y2 = 1;    % 当-1<=t & t<1时
y3 = -t+2; % 当1<=t & t<2时
y = y1.*(-2<=t&t<-1) + y2.*(-1<=t&t<1) + y3.*(1<=t&t<2);% 分段函数的实现：小括号内为处置序列，true返回1，false返回0
x = y.*( u(t+2) - u(t-2) ); % x为有限长的信号，只取-2到2
subplot(2,2,1.5);
plot(t,x); title('时域：x(t)'),axis([-5,5,-1,1]),xlabel('t')
grid on
% for k = -4*pi:dw:4*pi
%     X(floor((k+4*pi)/dw+1)) = x*exp(-j*t'*k)*dt; % 类比上面的傅里叶级数
% end
X = x*exp(-j*t'*w)*dt; % 第二种实现方法（求傅里叶级数也可以这么实现） 
    %  先通过t'*w实现一个length(x)×length(x)的矩阵，和x相乘后得到1×length(x)的矩阵，即傅里叶变换结果X
    % 注意这里的t'*w不能写成w*t'（矩阵乘法不满足交换律）
subplot(223)
plot(w,abs(X));xlabel('w');title('幅度谱')
grid on
subplot(224)
plot(w,angle(X));xlabel('w');title('相位谱')

3）实验二_1：

计算傅里叶级数后，利用傅里叶级数合成信号。并观察谐波次数N对合成信号的影响

T = 2;
dt = 0.00001;
t = -2:dt:2;
x0 = u(t) - u(t-1-dt); % 一个周期的信号。一定要-dt
%% 画出原信号
x = 0;
% 周期延拓
for m = -1:1
   x = x + u(t-m*T) - u(t-m*T-1-dt);
end
subplot(221);plot(t,x);
N = 10; % 谐波次数
w0 = 2*pi/T;
%% 
for k = -N:N
    ak(N+1+k) = (1/T)*x0*exp(-j*k*w0*t')*dt; % 注意要乘以w0角频率
end
subplot(222);stem([-N:N],abs(ak));
%% 画幅度谱
phi = angle(ak);
subplot(223);stem([-N:N],phi);
%% 画相位谱
x2 = zeros(1,length(t));
for m = -2:dt:2
    x2(round((m+2)/dt) + 1) = 0;  % 注意这里要用round四舍五入！不能用floor向下取整
    for k = -N:N  % 求每一个t对应的x2(t)：将各次谐波[-N:N]的信号加起来
        x2(round((m+2)/dt) + 1) = x2(round((m+2)/dt) + 1) + ak(k+N+1)*exp(j*k*w0*m);% 通过合成信号的公式合成
    end
end
subplot(224);plot(t,x2); % 画出合成信号。谐波次数N越大，效果越好

4 Z变换（见DSP4_ZTransform.m）

1）求离散时间系统的Z变换乘积

% 频域的乘积即时域的卷积
x1 = [1,2,3];n1 = [-1:1]; % 离散时间信号（即序列）x1和对应的自变量n1.其中2是原点
x2 = [2,4,3,5];n2 = [-2:1]; % x2和对应的自变量n2，其中3是原点
[x3,n3] = conv_m(x1,n1,x2,n2) % 输出卷积结果x3与对应的自变量n3
% 输出结果为：
% x3 = [2,8,17,23,19,15]
% n3 = [-3,-2,-1,0,1,2]

结果为：

2）部分分式法：求X(z)的部分展开式

b = [1.5,0.98,-2.608,1.2,-0.144];  % b是分子系数矩阵，降幂排列
a = [1,-1.4,0.6,-0.072]; % a是分母系数矩阵，降幂排列
[r,p,k] = residuez(b,a) % residuez用于求z变换结果X(z)的部分展开式
% 其中r是留数，p是极数，k是常数
% 输出结果为：
% r = [0.7,0.5,0.3]
% p = [0.6,0.6,0.6]
% k = [0,2]

                    ![在这里插入图片描述](https://img-blog.csdnimg.cn/20200430160801988.png#pic_center)

3）实验三_3 ：计算零极点与系统稳定性

b = [0,1,2,1];  % 分子系数矩阵，降幂
a = [1,-0.5,-0.005,0.3]; % 分母系数矩阵，降幂
[z,p,k] = tf2zp(b,a);    % 计算零极点的函数，z为零点，p为极点
zplane(b,a);title('零极点分布图');  % 通过zplane函数画出零极点分布图
% 输出结果为：
% 零点： -1，-1
% 极点： 0.5198 + 0.5346i，0.5198-0.5346i，-0.5396

             ![在这里插入图片描述](https://img-blog.csdnimg.cn/20200430160918713.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0RhYmllX2hhemU=,size_16,color_FFFFFF,t_70#pic_center)

图中○表示零点，×表示极点。由于极点都在单位圆内，所以系统稳定。

5 LTI系统的频域分析（见DSP5_LTISpectrumAnalysis.m）

1） 根据h(n)求系统频域响应H(exp(j*w))的幅度响应和相位响应

% 原信号是非周期的，因此频域上连续
% 求系统函数的方法一：手算
w = [0:500]*pi/500;  % 模拟频域上的连续，范围0-pi 
H = exp(j*w)./(exp(j*w)-0.9*ones(1,501));  % 首先手算出系统函数H，注意为了保持矢量一致，常数0.9要乘以ones(1,501)
% 求系统函数方法二：用freqz函数
b = [1,0];
a = [1,-0.9];
[H,w] = freqz(b,a); % freqz函数用于求系统的频响特性，返回值H是对应于频点w的频响值
subplot(2,1,1)
plot(w/pi,abs(H));title('幅度响应');xlabel('w（单位：π）')    % 画出系统函数H的幅度响应，为了显示好看，将频点除以pi归一化
subplot(2,1,2)
plot(w/pi,angle(H));title('相位响应');xlabel('w(单位：π)')

2）实验四_1（问题a和上面的差不多，主要看问题b）：

b = [1 0];
a = [1 -0.8];
%% 求频率特性
figure(1)
[H,w] = freqz(b,a,200);
subplot(211)
plot(w/pi,abs(H));grid;
xlabel('w(单位:π)');ylabel('幅度|H|');title('幅度响应');
subplot(212)
plot(w/pi,angle(H)/pi);grid;
xlabel('w(单位：π)');ylabel('相位(rad/π)');title('相位响应');
%% 求稳态响应
n = 0:220;   % 时域序列的时域点
Xn = cos(0.05*pi*n).*u(n); % 系统的输入序列，注意逐项相乘要用点乘.
y = filter(b,a,Xn); %  实现差分方程的求解，其中b和a分别是差分方程的输出y和输入x的系数，Xn是输入信号，y是通过该系统的时域响应
figure(2);
stem(n,y,'filled');axis([75,220,-5,5]);
title('系统的响应');xlabel('n');ylabel('y(n)');grid on

3）实验四_2（典型例题）：

b = [1 0 -1];
a = [1 0 -0.81];
%% 求系统函数（频率特性）
figure(1)
[H,w] = freqz(b,a);
subplot(211)
plot(w/pi,abs(H));grid;
xlabel('w(单位:π)');ylabel('幅度|H|');title('幅度响应');
subplot(212)
plot(w/pi,angle(H));grid;
xlabel('w(单位：π)');ylabel('相位(rad/??)');title('相位响应');
%% 求单位脉冲响应:时域上是离散的
figure(2)
% 实现单位脉冲响应的方法一：直接用函数impz
impz(b,a,20) % 实现系统的冲激响应（即脉冲响应），b和a的参数分别为差分方程的输出y和输入x的系数向量，20表示脉冲响应输出的序列点数为20
% 实现单位脉冲响应的方法二：用函数filter，通过输入信号求输出
n = 0:20;
Xn = (n==0)
y = filter(b,a,Xn);stem(n,y)
 
title('单位脉冲响应');ylabel('h(n)');xlabel('n');
%% 求单位阶跃响应
n = 0:50;
Xn = u(n); % 系统的输入序列：单位阶跃信号
figure(3);
y = filter(b,a,Xn);% 实现差分方程的求解，同时也是求系统对某一输入Xn的响应。当Xn为单位阶跃信号时，输出的就是单位阶跃响应
stem(n,y,'filled');
title('单位阶跃响应');ylabel('v(n)');xlabel('n')

6 简单滤波器设计（见DSP6_SimpleFilterDesign.m）

1）设计一个高通滤波器，滤去低频分量

w1 = 0.015*pi; % 第一个角频率
w2 = 0.4*pi; % 第二个角频率
N = 50;     % 时域的序列点数
% 为了滤去低频分量，系统需要满足A.*x = B，其中矩阵A和B的值的计算见下面
A = [2*cos(w1) 1; 2*cos(w2) 1]; % 第一个矩阵2*2，所以中间要用分号表示换行
B = [0;1];  % 得到的乘积矩阵1*2，所以中间要用分号表示换行
x = A\B    % A.*x = B,要得到矩阵x，x = A\B，矩阵x即[α；β]
% 输出的x为：
% [-0.7248;1.4479];即α = -0.7248，β = 1.4479
% 对应的差分方程为：y[k] = x(1)*x[k] + x(2)*x[k-1] + x(1)*x[k-2]
a = 1;  % 差分方程输出y的系数矩阵
b = [x(1) x(2) x(1)];  % 差分方程输出x的系数矩阵
% 产生两个正弦信号
n = 0:N;    % 时域序列点
x1 = cos(w1*n);   % 低频分量
x2 = cos(w2*n);   % 高频分量
% 信号滤波（主要利用系统函数，反映在函数中就是b和a的取值）
y = filter(b,a,x1+x2);  % x1+x2
plot(n,y,'r',n,x2,'b--',n,x1+x2,'k:') % 冒号表示虚线
ylabel('幅度');xlabel('n');
legend('y[n]','x2[n]','x1[n]+x2[n]'); % 分别对应1,2,3
% 调用firl函数，进行信号滤波
wn=[0.3 0.5]; % wn是对π归一化的数字频率。需要得到0.4的，滤掉0.1和0.7的，所以把带宽设置在0.3-0.5
b2 = fir1(20,wn,'bandpass');% 第一个参数不知道是啥，就写20，第三个参数写带宽 'bandpass'
y2 = filter(b2,a,x1+x2);
figure(2)
plot(n,y2,'r',n,x2,'b--',n,x1+x2,'k:');% 冒号表示用虚线
ylabel('????');xlabel('n');
legend('y2[n]','x2[n]','x1[n]+x2[n]');% 分别对应1,2,3

                    ![在这里插入图片描述](https://img-blog.csdnimg.cn/20200430161210957.png#pic_center)

由上式可知系统的群时延为

为了滤除低频分量，系统需满足：

对应的代码内容是A.*x = B

7 信号的采样和重建

1）对信号x(t)进行采样和重建

%% 对信号进行采样与重建
% 描述原始信号
T = 2; % T是时域信号取出来的总时间，这个长度是自己定的，一般要包含一个周期
dt = 0.02;
t = -T:dt:T; % 模拟时域上的连续
x = (1+cos(pi*t)).*(u(t+1)-u(t-1)); % 原始信号的表示
subplot(221);
plot(t,x);axis([-2,2,-0.5,2.5]);
title('x(t)');
 
% 画出原始信号的频谱，找出其最高频率
% 信号在时域上是连续非周期的，在频域上是离散非周期的
w = -4*pi:0.1*pi:4*pi;
X = x*exp(-j*t'*w)*dt; % 用傅里叶变换的公式求出频谱X
subplot(222);
plot(w/pi,abs(X));title('X(jw)') % 画出原始信号的频谱，发现最高频率差不多是2*pi
 
% 进行时域采样
wm = 2*pi; % 根据原始信号的频谱确定信号x(t)的最高频率
ws = 2*wm; % 采样频率
Ts = 2*pi/ws; % 采样周期，相当于是时域采样的间隔
N = fix(T/Ts); % 确定采样点数：信号时长是T，采样周期是Ts,采样点数就是N。其中fix是向0取整
n = -N:N;    % 对应采样公式里的n，也是采样信号的因变量
xs = (1+cos(pi*n*Ts)).*(u(n*Ts+1) - u(n*Ts-1)); % 根据采样公式，采样后的信号就是将原信号的t替换成n*Ts。注意这里要将范围限制在[-1/Ts,1/Ts]
subplot(223)
stem(n,xs);title('xs(n)')
 
% 进行重建
xr = zeros(1,length(t));
L = length(-N:N);   % xs对应的自变量长度
wc = wm;   % 理想低通滤波器的截止频率
for i=1:L  % i是当前循环中xs(n*Ts)对应的xs中的下标索引
   m = i-((L-1)/2+1); % m是当前n的数值，范围是[-N:N]
   xr = xs(i)*((wc)*Ts)*sinc(wc*(t-m*Ts)/pi)/pi + xr; % 利用重建公式计算重建后的信号。注意这里的sinc函数不是简单的Sa函数，括号里还要除以pi
end
subplot(224)
plot(t,xr);title('xr(t)')

8 信号DFT的计算

1）用DFT计算有限长余弦信号的频谱

N = 20; % 时域采样的点数
L = 64; % 频域采样的点数
f1 = 100; f2 = 120; % 信号的两个频率
fs = 600;  % 采样频率
Ts = 1/fs; % 采样周期
ws = 2*pi*fs; % 采样角频率
t = (0:N-1)*Ts;  % 时域采样序列的自变量
f = cos(2*pi*f1*t) + cos(2*pi*f2*t); % 采样得到的时域序列
F = fft(f,L); % 用fft实现。其中L为频域采样的点数
F = fftshift(F);% fftshift的作用是让正半轴部分和负半轴部分的图像分别关于各自的中心对称
wm = ws/2; % 信号的显示部分最高频率（包含了信号的最高频率）
w = ( -wm + 2*wm*(0:L-1)/L )/(2*pi); % 频率（不是角频率）的范围[-wm,wm]，单位是Hz
plot(w,abs(F)/N);xlabel('Hz');ylabel('Amp')

9 加窗对信号频谱分析影响

1）在DFT对信号进行频谱分析时，分别加矩形窗和海明窗

%% 加矩形窗
f1 = 100;f2 = 150;
fs = 600;Ts = 1/fs; ws = 2*pi*fs;
N = 25; % 时域采样点数
n = 0:N-1; % 注意这里是0：N-1，不是1：N，也不是-N:N
x = cos(2*pi*f1*n*Ts) + 0.15*cos(2*pi*f2*n*Ts); % 加矩形窗就是截断，不需要用专门的函数
L = 25; % 频域采样点数设为和时域采样点数一样
F = fftshift(fft(x,L));
w = ( -ws/2 + ws*(0:L-1)/L )/(2*pi);  % 注意这里是0：L-1，别误写成0：L
subplot(2,2,1.5)
plot(w,abs(F)/N);title('N=25 矩形窗')
%% 加海明窗（和矩形窗代码基本一致，只是加窗不同）
f1 = 100;f2 = 150;
fs = 600;Ts = 1/fs; ws = 2*pi*fs;
N = 25; 
n = 0:N-1; 
x = (cos(2*pi*f1*n*Ts) + 0.15*cos(2*pi*f2*n*Ts)).*hamming(N)'; % 用函数hamming加上海明窗，注意是点乘，并且hamming参数是N，还要转置
L = 25; 
F = fftshift(fft(x,L));
w = ( -ws/2 + ws*(0:L-1)/L )/(2*pi);  
subplot(2,2,3.5)
plot(w,abs(F)/N);title('N=25 海明窗')

10 数字滤波器结构

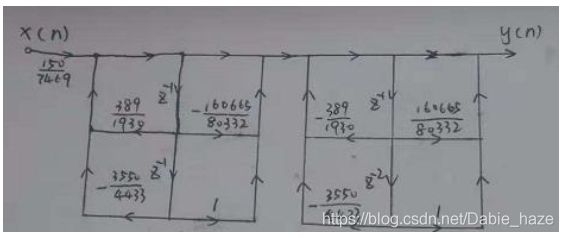
1）实现IIR滤波器的级联型和并联型结构

format rat   % 将所有输出都写成分式，更准确（下面的输出结果都是小数形式，没有改过来）
%% 描述系统函数
b = [0.020083,0,-0.040167,0,0.020083]; % 分子系数向量
a = [1,0,1.561,0,0.6413];  % 分母系数向量
 
%% 实现级联型结构：转换成二次项分式相乘
[z,p,k] = tf2zp(b,a);   % 由于转换成二次项分式的函数zp2sos的输入是零极点，所以先用此函数求零极点
sos = zp2sos(z,p,k)    % 将系统的零极点转换为二次项分式的系数矩阵sos
% sos的输出结果为：
% sos =
% [0.0201 -0.0402 0.0201   1 -0.2016 0.8008;
%  1      2       1        1 0.2016  0.8008]
 
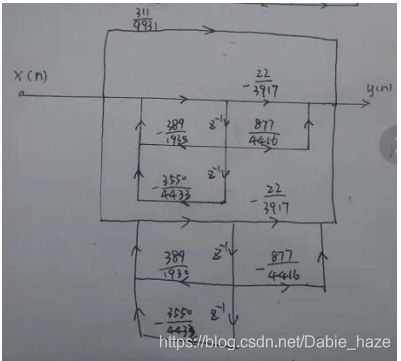
%% 实现并联型结构：展开成部分分式相加
[r,p,k] = residuez(b,a) %  用residuez使用部分分式法将系统函数展开，得到的r是留数，p是极点，k是常数
% 输出结果为：
% r = [-0.0028-0.1120i,-0.0028+0.1120i,-0.0028+0.1120i,+0.0028-0.1120i]
% p = [-0.1008+0.8892i,-0.1008-0.8892i, 0.1008+0.8892i, 0.1008-0.8892i]
% k = 0.0313
 
% 由于留数r和极点p的输出中有共轭复数，为了实现方便，需要将共轭复数转换为实数
[b1,a1] = residuez([r(1),r(2)],[p(1),p(2)],0)
[b2,a2] = residuez([r(3),r(4)],[p(3),p(4)],0)
% 输出结果为：
% b1 = [-0.0056,0.1986,0]
% a1 = [1,0.2016,0.8008]
% b2 = [-0.0056,-0.1986,0]
% a2 = [1,-0.2016,0.8008]

二次项分式为：

级联型结构为：

展开的部分分式为：

并联型结构为：

11 FIR数字滤波器的设计

1）用窗函数法设计FIR数字滤波器：

wp = 0.2*pi; % 通带截止频率
ws = 0.3*pi; % 阻带截止频率
tr_width = ws-wp; % 过渡带宽
N = ceil(6.6*pi/tr_width) + 1;  % 根据过渡带宽度确定N值：海明窗的过渡带宽是6.6*pi/N，即d_width = 6.6*pi/N，这里求N需要ceil向上取整再+1
n = 0:N-1;
wc = (wp+ws)/2; % 求理想低通的截止频率：通带截止频率和阻带截止频率的平均值
hd = ideal_lp(wc,N);  % 求出理想的单位抽样响应hd(n)
h = hd.*(hamming(N)'); % 求出所涉及的FIR滤波器的单位抽样响应h
[db,mag,pha,grd,w] = freqz_m(h,[1]); % 计算频率响应，其中w是频谱上对应的频点，这行代码背下来。。。
% delta_w = 2*pi/1000;
% Rp = -(min(db(1:wp/delta_w+1))); % 求出实际的阻带衰减
% As = -round(max(db(ws/delta_w+1 : 501))); %
% 画出理想的单位抽样响应hd(n)
subplot(221)
stem(n,hd);
title('Ideal Impulse Response');axis([0 N-1 -0.1 0.3]);xlabel('n');ylabel('hd(n)');
% 画出海明窗
subplot(222)
stem(n,(hamming(N))');
title('Hamming Window');axis([0 N-1 0 1.1]);xlabel('n');ylabel('w(n)');
% 画出设计的FIR滤波器的单位抽样响应（理想单位抽样响应与海明窗相乘的结果）
subplot(223)
stem(n,h);
title('Actual Impulse Response');axis([0 N-1 -0.1 0.3]);xlabel('n');ylabel('h(n)');
% 画出每dB上的响应
subplot(224)
plot(w/pi,db);
title('Magnitude Response in dB');axis([0 1 -100 10]);xlabel('frequency/pi');ylabel('dB');

2）频率取样法设计FIR数字滤波器

% 一般高通都设计为h(n)偶对称，H(w)的对称性再结合N决定
N = 33; % 采样点
ws = 0.5*pi; % 阻带截止频率
wc = 0.6*pi; % 通带截止频率
N1 = fix(N*ws/(2*pi)));% 阻带上采样点
N2 = N - fix(N*wc/pi); % 通带上采样点，注意这里fix的位置
N3 = fix((N-2*N1-N2)/2); % 过渡带上采样点
A = [zeros(1,N1),[1:N3]/N3,ones(1,N2),1-[1:N3]/N3,zeros(1,N1)]; % A是幅度，即abs(H)
theta = -pi*[0:N-1]*(N-1)/N; % 线性相位约束条件
H = A.*exp(j*theta);% 求频谱函数H = A*e^(jφ)
h = real(ifft(H)); % 傅里叶逆变换，求脉冲响应
 
subplot(211);
plot([1:N],A,'*') % 画幅度谱
title('N=33');axis([0,fix(N*1.1),-0.1,1.1]);ylabel('H(k)');
subplot(212)
stem([1:N],h); % 画脉冲响应h(n)
title('');ylabel('h(n)');

12 IIR数字滤波器的设计

1）用模拟滤波器（这里分别用巴特沃斯、切比雪夫I型、椭圆型）转换数字滤波器的方法（脉冲响应不变法和双线性变换法）

%% 待设计的IIR滤波器指标
wp = 0.2; % 归一化通带截止频率
ws = 0.4; % 归一化阻带截止频率
Ap=0.5;   % 通带最大衰减
As=20;    % 阻带最大衰减
fs = 1;   % 采样频率，一般都设成1
%% 选用的模拟滤波器
% 巴特沃斯模拟滤波器，函数为buttord和butter
[N,wc]=buttord(wp,ws,Ap,As,'s'); % 输入分别归一化的通带和阻带频率，通带和阻带的衰减，'s'表示是模拟的
[b,a]=butter(N,wc,'s'); % 输入是上一个函数的输出，N表示滤波器的阶数，wc表示3dB截止频率；输出b和a分别是滤波器系统函数的分子和分母系数向量
% 切比雪夫I型模拟滤波器，函数为cheb1ord和cheby1
[N,wc]=cheb1ord(wp,ws,Ap,As,'s');
[b,a]=cheby1(N,Ap,wc,'s'); % 输入除了N和wc，中间还加一个参数：通带最大衰减Ap
% 椭圆型模拟滤波器，函数为ellipord和ellip
[N,wc]=ellipord(wp,ws,Ap,As,'s');
[b,a]=ellip(N,Ap,As,wc,'s'); % 输入除了N和wc，中间加入通带和阻带衰减Ap,As
%% 将模拟滤波器转换为数字滤波器的两种方法
% 脉冲响应不变法，函数为impinvar
[bt,at]=impinvar(b,a,fs); % 输入是对应模拟滤波器系统函数的分子和分母系数向量以及采样频率，输出是转换后的数字滤波器系统函数的分子和分母系数向量
figure(1),freqz(bt,at);title('脉冲响应不变法'); % 用freqz画出系统函数对应的频谱
% 双线性变换法，函数为bilinear
[bt2,at2]=bilinear(b,a,fs);
figure(2),freqz(bt2,at2);title('双线性变换法');
%% 最后看看用官方函数直接画出的数字滤波器（类似模拟滤波器的函数，只是没有最后一个参数's'）
% 巴特沃斯数字滤波器
[N,wc]=buttord(wp,ws,Ap,As); 
[b,a]=butter(N,wc);
% 切比雪夫I型数字滤波器
[N,wc]=cheb1ord(wp,ws,Ap,As);
[b,a]=cheby1(N,Ap,wc);
% 椭圆型数字滤波器
[N,wc]=ellipord(wp,ws,Ap,As);
[b,a]=ellip(N,Ap,As,wc);