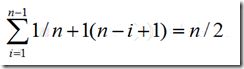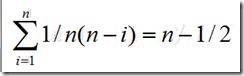数据结构系列2------线性表

1.定义

线性表是n(n≥0)个数据元素的有序系列。特点是数据元素之间是一种线性关系，数据元素"一个接一个的排列"。再一个线性表中，数据元素的类型是相同的，或者说线性表是由同一类型的数据构成的线性结构。例如：阿拉伯数字、26个字母、一个星期的7天等。通常记作：(a1,a2,a3….ai,an-1),n为表长,n=0时为空表。

表中相邻元素之间存在顺序关系。它主要有3个特点，分别是：

1):同一性，同一线性表中的数据元素具有相同类型。

2):有穷性，个数有限。

3):有序性，除了头尾元素，其它元素有且只有唯一直接前趋和直接后趋。

假设线性表中的每一个数据元素需要占用1个存储单元，并以所占的第一个单元的存储地址作为数据元素的存储位置，那么第N个数据元素的存储位置为：

Loc(a_n)=Loc(a₀)+i*1

Loc(a₀)表示第一个数据元素的存储位置，通常叫做起始位置或首地址.

.net中线性表有ArrayList、List<T>等。

1):ArrayList:在System.Collections命名空间下，AllayList的Capacity属性值默认为16，如果不够则加倍。它使用Object类型存储对象。

公共构造、属性、方法我就不详细写了，具体MSDN。

2):List<T>:C#2.0增加了泛型（Generics在)。在命名空间 System.Collections.Generic下，它能提供比非泛型集合更好的类型安全性和性能。 List<T>类是ArrayList类的泛型等效类，表示可通过索引访问的对象的强类型列表，List<T>在大多数情况下比ArrayList执行得更好并且是类型安全的。 List<T>类所具有的属性和方法非常类似于ArrayList类对应的属性和方法，差别在于前者是强类型列表，元素的类型要与列表定义时声明的类型保持一致。

在第i(0≤i≤n-1)个元素之前插入一个元素，需要把第i到第n-1个元素后移1一个位置。删除既向前移一个位置。具体代码不贴，请自行实现。

判断顺序表的空状态，返回顺序表的长度，获取或设置指定位置的数据元素值等操作都与数据元素的个数无关，所以时间复杂度为O(1)。而在线性表中查找给定值，插入和删除数据元素等操作都与数据元素的个数有关，时间复杂度为O(n)。

假设在任何位置插入都是等概率，如果在每个元素之前插入元素的概率是1/n+1.在表中第i(1≤i≤n-1)个元素之前插入一个节点的移动次数为n-(i-1)，所以在长度为n的线性表中插入一个元素所需要移动元素的平均次数为：

E= 。

假设在任何位置上删除等概率，则删除任何一个元素的概率是1/n，删除第i个元素的元素移动次数为n-i，则在长度为n的线性表中删除一个元素需要移动元素的平均次数为：

E= 。

因此，在线性表中，插入或删除一个元素平均移动表中一半元素。当N较大时，算法效率很低。因此，线性表一般不用于表较大、频繁插入、删除的情况。

经典算法之：约瑟夫环（Josephus）问题。

问题描述：古代某法官要判决n个犯人的死刑，他使用了一条荒唐的方法，让犯人站成一个圆圈，从第s个人开始数起，每数到第d个犯人，就拉出来处决，然后再数d个，数到的人再处决……直到剩下的最后一个人可以得到赦免。

代码如下：

        //思路：用有N个元素的线性表表示N个人，采用取模运算实现环形计数。

        static void Main(string[] args)

        {

            Josephus(5, 1, 2);

        }

        /// <summary>

        /// 约瑟夫环算法

        /// </summary>

        /// <param name="n">n个犯人</param>

        /// <param name="s">从第s个人开始</param>

        /// <param name="d">数到第d个犯人</param>

        public static void Josephus(int n, int s, int d)

        {

            var aList = new ArrayList();

            int i, j, k;

            for (i = 1; i <= n; i++)

            {

                aList.Add(i);

            }

            i = s - 2;//因为第s个人的下标为s-1,i初始值指向第s个人的前一位置。

            k = n;//每一轮的当前人数

            while (k > 1)//n-1个人依次出环

            {

                j = 0;

                while (j < d)

                {

                    j++;

                    i = (i + 1) % k;

                }

                aList.Remove(i);

                k--;

                i = (i - 1) % k;

            }

            var lastPeople = aList[0];

            Console.WriteLine(lastPeople);

            Console.ReadLine();

        }

下期更新栈和队列。