1 概念
- 堆:即优先队列,是基于完全⼆叉树所定义的一种新的数据结构,其要求完全二叉树中的任意三元组的根节点都是极大(小)值,并且树的根节点是最大(小)值。
2 分类
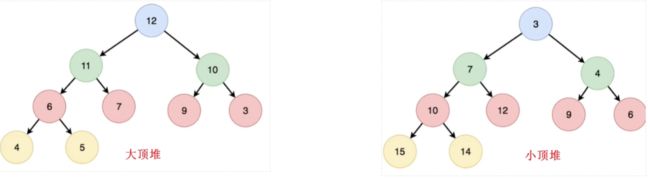
- ⼤顶(根)堆:在堆中,任意三元组中的根节点都是极⼤值,其可以求取全局最大值、全局次最大值。
- ⼩顶(根)堆:在堆中,任意三元组中的根节点都是极小值,其可以求取全局最小值、全局次最小值。
3 建堆方法
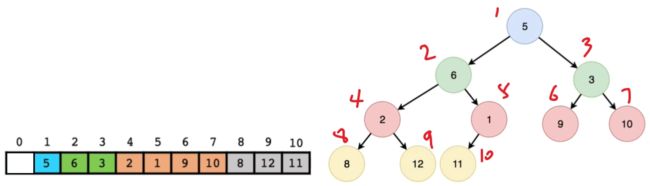
- 利用数组表示一颗完全二叉树,其表示关系为:根节点i,左孩子2i,右孩子2i+1,i≥1。
3.1 堆尾插入元素建堆法(自顶向下)
- 条件:事先不知道有多少个元素,通过动态的往堆里面插入元素进行调整来构建堆。
- 构建过程:(堆调整顺序:自下向上)
- 在堆尾插入新的元素;
- 当前元素存在父节点,执行步骤3,否则建堆结束;
- 比较当前元素和它的父结点值;如果当前元素比父节点值大,则交换两个元素(大顶堆),并继续执行步骤2,否则建堆结束。
- 大顶堆插入元素示意图:
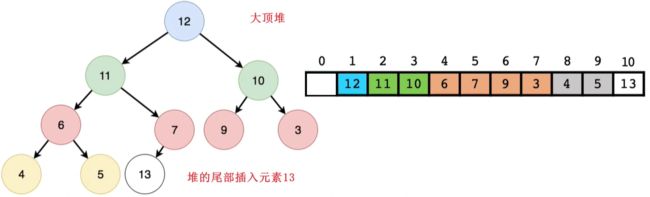
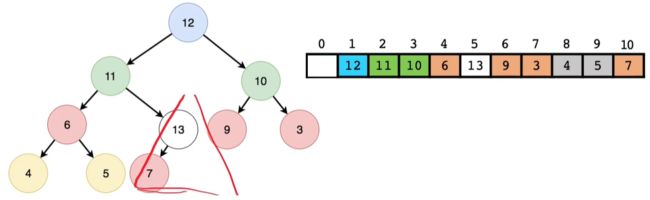
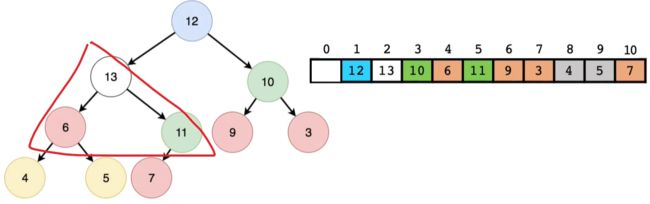
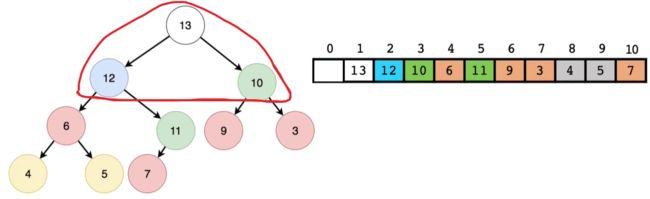
- 经过堆调整后的结果展示:
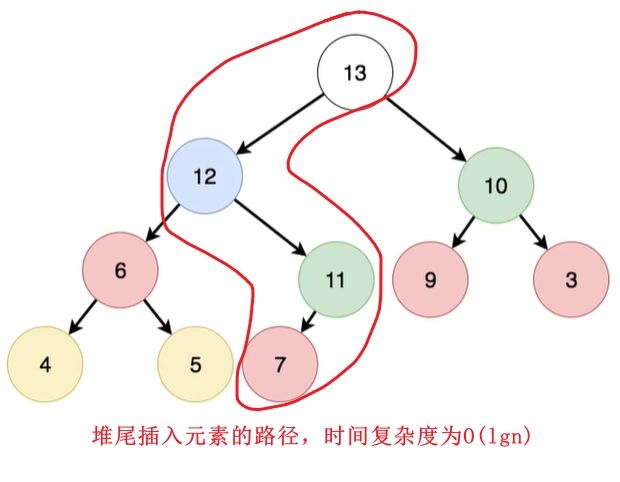
- 从图中可以看出,从堆尾插入元素并进行堆结构调整,其时间复杂度为o(lgn),n为节点个数;
3.2 线性建堆法(自下向上的)
- 条件:堆元素已经确定好的情况下,使用线性建堆法,如堆排序;
- 构建过程:
- 找到最后1个元素的父节点(parent_node ),即当前堆大小的一半(n/2),记作parent_node = n >> 2,n为堆中的节点大小;
- 从parent_node = (n / 2)位置开始,自上向下的调整堆结构,直到parent_node = 0为止;(遍历条件:1 ≤ parent_node ≤ n / 2 )
- 大顶堆建堆示意图:
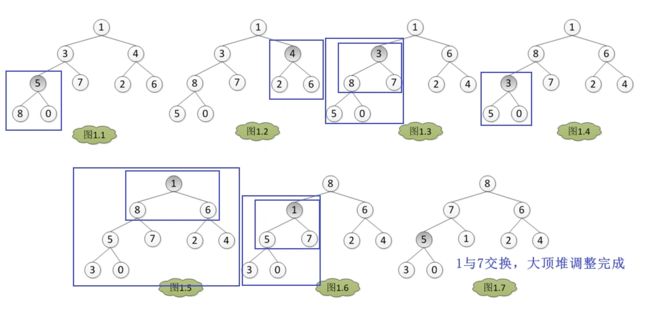
3.3 两种建堆方法的时间复杂度分析
在树高为h的二叉树中,根节点为第1层,每层的节点数量为2^(N-1),其中N为每层的编号,N∈[1, h]。
- 树的高度与节点关系为:
\[s_n = \sum_{N=1}^h2^{(N-1)} = 2^0 + 2^1 + 2^2 + ... + 2^{(h-2)} + 2^{(h-1)} = 2^h - 1,N∈[1, h] \]
\[h = log_2(s_n+1) \]
3.3.1 插入建堆法的时间复杂度分析- o(n*logn)
\[T = (N-1)*2^{(N-1)} + (N-2)*2^{(N-2)} + (N-3)*2^{(N-3)} + .... + 1*2^1 + 0*2^0 \]
- 上式中,每项的第1个参数:该节点向上调整的次数,每项的第2个参数:该层的节点数目;如第1项,(N-1)*2^(N-1) 表示第N层有2^(N-1)个节点需要经过(N-1)次向上堆调整过程。
\[T' = 2*T = (N-1)*2^{N} + (N-2)*2^{(N-1)} + (N-3)*2^{(N-2)} + .... + 1*2^2 + 0*2^1 \]
\[T = T'-T = (N-1)*2^{N} -(2^{(N-1)} + 2^{(N-2)} + .... + 2^2 + 2^1) = (N-1)*2^{N} + (2 - 2^{N}) = N*2^{N} + 2^{(N+1)} +2 \]
\[o(T) = o(h*2^h - 2^{(h +1)} + 2) ≈ o(h*2^h) = o((s_n+1)*log_2(s_n+1))=o(nlog_2n) \]
3.3.2 线性建堆法的时间复杂度分析:- o(n)
\[T = 0*2^{(N-1)} + 1*2^{(N-2)} + 2*2^{(N-3)} + .... + (N-2)*2^1 + (N-1)*2^0 \]
- 上式中,每项的第1个参数:该层节点向下调整的次数,每项的第2个参数:该层的节点数目
\[T' = 2*T = 1*2^{(N-1)} + 2*2^{(N-2)} + .... + (N-2)*2^2 + (N-1)*2^1 \]
\[T = T'-T = 2^{(N-1)} + 2^{(N-2)} + .... + 2^2 + 2^1 - (N-1)*2^0 = 2^N - N - 1 \]
\[o(T) = o(2^h - h -1) ≈ o(2^h) = o(s_n+1)=o(n) \]
- 时间复杂度结论:插入建堆 — o(nlgn),线性建堆 — o(n),n为节点个数
4 删除堆顶元素- o(logn)
- 删除步骤:
- 用堆尾元素替换堆顶元素,并将堆大小减1;
- 自上向下的调整堆结构,保证任意一个三元组都满足堆性质;
- 在当前节点编号大于节点数量 或 调整堆结构已发现满足堆性质时,停止调整,否则继续执行步骤2。
- 删除堆顶元素的示意图:
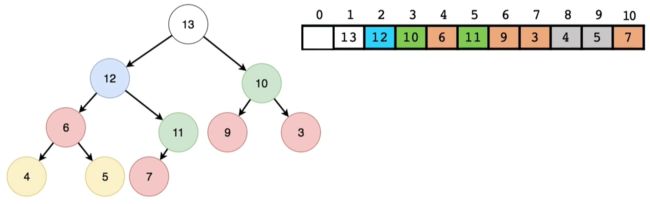
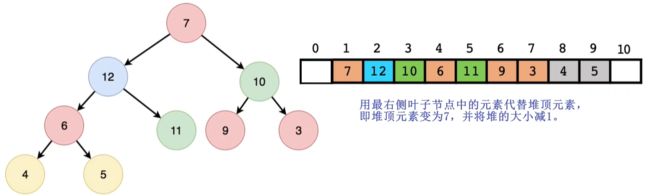
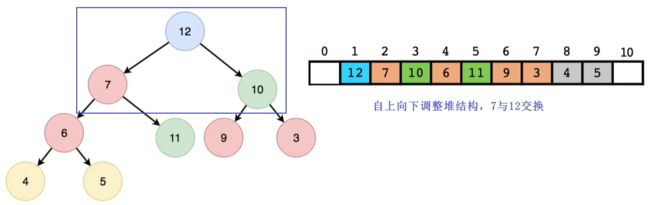
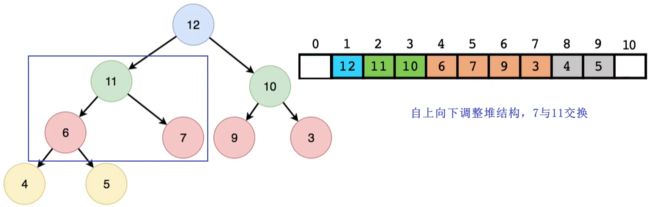
- 结论:删除堆顶元素需要自上向下调整堆结构,其时间复杂度为o(lgn),n为节点数目
5 堆排序 - o(n*logn)
- 堆排序步骤:
- 将堆顶元素与堆尾元素交换;
- 对前n-1元素重新建堆;(与删除堆顶元素后的堆调整过程一样)
- 重复1、2 两个过程,直到堆中的元素为1时停止;
- 结论:采取大顶堆的调整方式,为升序排序;而采取小顶堆的调整方式,为降序排序。
6 代码演示
6.1 插入建堆法
#include
#include
#include
#define SWAP(a, b) {\
__typeof(a) __temp = a; a = b; b = __temp;\
}
typedef struct priority_queue {
int *data;
int cnt, size; // cnt:堆中的元素个数,size:堆空间的容量
} priority_queue;
priority_queue* init(int size) {
priority_queue* q = (priority_queue*)malloc(sizeof(priority_queue));
// 多申请1个空间,是因为堆顶元素的编号为1,这样在建堆过程中可以减少1次加法运算
q->data = (int*)malloc((size + 1) * sizeof(int));
q->cnt = 0;
q->size = size;
return q;
}
int empty(priority_queue* q) {
return q->cnt == 0;
}
// 获取堆顶元素
int top(priority_queue* q) {
return q->data[1];
}
// 堆尾插入元素
int push(priority_queue* q, int v) {
if (q == NULL) return 0;
if (q->cnt == q->size) return 0;
// 将元素插入堆尾
q->data[++(q->cnt)] = v;
// 重新调整堆结构(大顶堆)--- 自下向上
int ind = q->cnt; // 获取当前元素的编号
while (ind >> 1 && q->data[ind] > q->data[ind >> 1]) {
SWAP(q->data[ind], q->data[ind >> 1]);
ind = ind >> 1;
}
return 1;
}
// 删除堆顶元素
int pop(priority_queue* q) {
if (q == NULL) return 0;
if (q->cnt == 0) return 0;
// 将堆尾元素赋值堆顶
q->data[1] = q->data[(q->cnt)--];
// 重新调整堆结构(大顶堆)--- 自上向下
int ind = 1; // 堆顶元素的编号
while ((ind << 1) <= q->cnt) {
int temp = ind, lnode = ind << 1, rnode = ind << 1 | 1;
if (q->data[temp] < q->data[lnode]) temp = lnode;
if (rnode <= q->cnt && q->data[temp] < q->data[rnode]) temp = rnode;
if (temp == ind) break; // 当前三元组结构未发生变化
SWAP(q->data[temp], q->data[ind]);
ind = temp;
}
return 1;
}
void clear(priority_queue* q) {
if (q == NULL) return ;
if (q->data) free(q->data);
free(q);
}
int main() {
srand(time(0));
const int N = 10;
priority_queue* q = init(N);
for (int i = 1; i <= N; i++) {
int v = rand() % 100;
push(q, v);
}
for (int i = 1; i <= q->cnt; i++) {
printf("%d ", q->data[i]);
}
printf("\n");
while (!empty(q)) {
printf("%d ", top(q));
pop(q);
}
printf("\n");
clear(q);
return 0;
}
6.2 堆排序(线性建堆法)
#include
#include
#include
// 线性建堆法:建堆时间 o(n)
// 堆排序:建堆时间 + 堆排序时间 = o(n) + o(n*lgn) = o(n*lgn)
#define SWAP(a, b) {\
__typeof(a) __temp = a; a = b; b = __temp;\
}
// 根节点:i,左子树节点:2*i,右子树节点:2*i+1,i >= 1;
// arr:输入数组,n:数组元素的个数,ind:代表完全二叉树的节点编号
void downUpdate(int *arr, int n, int ind) {
// ind << 1:下一层节点编号,即当前节点的左子树节点编号,其节点编号代表元素的个数
while ((ind << 1) <= n) {
int temp = ind, l = ind << 1, r = ind << 1 | 1; // l:下一层的左子树节点编号,r:下一层的右子树节点编号
// 大顶堆构建(堆排序:从小到大排序),任意三元组的父节点为极大值
if (arr[l] > arr[temp]) temp = l;
if (r <= n && arr[r] > arr[temp]) temp = r;
// 小顶堆构建(堆排序:从大到小排序),任意三元组的父节点为极小值
// if (arr[l] < arr[temp]) temp = l;
// if (r <= n && arr[r] < arr[temp]) temp = r;
if (ind == temp) break; // ind == temp:三元组中的父节点为极大(小)值节点
swap(arr[temp], arr[ind]);
ind = temp;
}
return ;
}
// arr:待排序的数组,n:数组元素的个数
void heap_sort(int *arr, int n) {
// 待排序的数组索引从0开始编号,而堆结构采取从1开始编号,故需要arr -= 1
arr -= 1;
// 线性建堆法 -- o(n)
for (int i = n >> 1; i >= 1; i--) {
downUpdate(arr, n, i);
}
// 堆排序的步骤:
// 1. 将堆顶元素与堆尾元素交换
// 2. 对前n-1元素重新建堆
// 3. 重复1、2 两个过程,直到堆中的元素为1时停止
for (int i = n; i > 1; i--) { // o(n * lgn)
swap(arr[i], arr[1]);
downUpdate(arr, i - 1, 1);
}
return ;
}
void output(int *arr, int n) {
printf("[");
for (int i = 0; i < n; i++) {
i && printf(" ");
printf("%d", arr[i]);
}
printf("]\n");
return ;
}
int main() {
srand(time(0));
#define MAX_N 10
int arr[MAX_N] = {0};
for (int i = 0; i < MAX_N; i++) {
arr[i] = rand() % 100;
}
output(arr, MAX_N);
heap_sort(arr, MAX_N);
output(arr, MAX_N);
#undef MAX_N
return 0;
}
7 总结
- 从堆尾插入元素,需要自下向上调整堆结构,需要o(logn)次;
- 从堆顶删除元素,需要自上向下调整堆结构,需要o(logn)次;
- 需要动态的往堆里插入元素时,采用插入建堆法【o(n*logn)】;
- 明确元素数量时,可以采用线性建堆法【o(n)】,如堆排序【o(n*logn)】;
- 堆之所以叫优先队列,是因为可以像队列从 堆尾插入元素、堆顶删除元素,并且每次出队权值都是最大(大顶堆)/最小(小顶堆)元素。