逻辑回归(使用激活函数sigmoid)详细介绍

线性回归预测得数字是连续的。
逻辑回归预测的是分类得问题。

一、引入

假设数据集如图。

如果使用线性回归进行预测

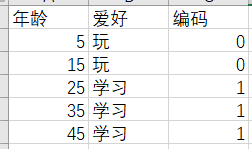
显然这种模型很难去准确预测各种年龄段的人爱好是什么。
我们的准确值是在0 1，而预测的是在负无穷到正无穷，显然很不符合。

二、sigmoid函数

通过上面看出，我们显然不能使用线性回归。我们可以使用逻辑回归中的sigmod函数来准确预测。(sigmod函数 重点！)
即 把结果 负无穷到正无穷 压缩到 0-1.（激活函数）

还拿上面的数据集来讲。




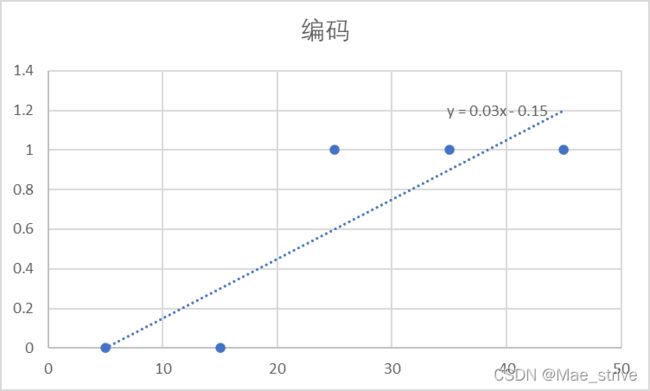
图像和上面不拟合的原因是我们选的m和b不好。(m=0.03 b=-0.15)

步骤与线性回归相似还是继续迭代m和b。

三、使用矩阵计算逻辑回归

Features为特征值矩阵(年龄) 5*1

Weights为m和b组成的向量(矩阵) 2*1

Labels为结果标签(0 1)(真实值) 1*1

为了方便计算，我们把Features矩阵都加一列1.

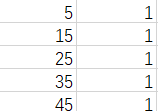
变成5*2矩阵

Features*Weights=mx+b
为什么？自己手写算一下就能得出来了

Features.T：Features矩阵的转置。
Features.T*Labels=MSE对b求导的结果(第一行)和MSE对m求导的结果(第二行)
为什么？自己手写算一下就能得出来了

四、代码实现

import numpy as np

data = np.array([
    [5, 0],
    [15, 0],
    [25, 1],
    [35, 1],
    [45, 1],
    [55, 1]
])

m = 1
b = 1

weight = np.array([
    [m],
    [b]
])

features = data[:, 0:1]
label = data[:, -1:]
# 拼一列1 axis:指定水平拼接
featureMatrix = np.append(features, np.ones(shape=(6, 1)), axis=1)
# 学习速率
lr = 0.001


def gradentDecent():
    # np.dot矩阵相乘
    predict = 1 / (1 + np.exp(-(np.dot(featureMatrix, weight))))
    # m的偏导 b的偏导
    return np.dot(featureMatrix.T, predict - label)


# 迭代m b的值
def train():
    for i in range(1, 10000000):
        slop = gradentDecent()
        global weight
        weight = weight - lr * slop
    print(weight)


if __name__ == '__main__':
    train()

迭代100万次 求出weight(m和b)

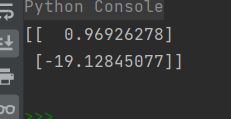
然后预测 某个年龄的爱好值
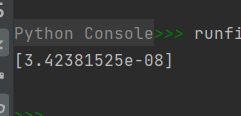
1、预测20岁的人学习的概率

import numpy as np

weight = np.array([[0.96926278],
                   [-19.12845077]])
# 预测20岁人 的爱好
features = np.array(
    [20, 1]
)

print(1 / (1 + np.exp(-np.dot(features, weight))))

2岁人学习的概率

import numpy as np

weight = np.array([[0.96926278],
                   [-19.12845077]])
# 预测2岁人 的爱好
features = np.array(
    [2, 1]
)

print(1 / (1 + np.exp(-np.dot(features, weight))))

接近于0了