机器学习公平性指标小结
文章目录
- 前言
- 一、Unawareness
- 二、individual fairness
- 三、group fairness
-
- 1. disparate impact
- 2. predictive equality
- 3. equal opportunity
- 4. disparate mistreatment
- 5. Predictive parity
- 四、causal fairness
-
- 1. proxy discrimination
- 2. unresolved discrimination
- 3. conterfectual fairness
- 一些参考文献
前言
机器学习系统中,如果模型的表现或模型的预测结果与敏感属性(性别、肤色等)有统计上的关联,那么这个机器学习系统就可能是不公平的:(1) Timbru等人发现一些商业的性别分类API中,白人的准确率明显高于有色人种;(2) Propublica等发现USA的犯罪预测系统COMPAS存在歧视黑人的现象,黑人的FPR高于白人。
一、Unawareness
Unawareness也叫blindness,既然敏感属性和预测结果有关联,不把敏感属性作为分类器的输入,能获得一定程度的公平,这种公平建立在“看不见”的基础上。当敏感属性与预测结果统计独立时,满足disparate treatment:
P ( y ^ ∣ x ) = P ( y ^ ∣ x , z ) P(\hat{y}|x)=P(\hat{y}|x,z) P(y^∣x)=P(y^∣x,z)
二、individual fairness
Dwork除了做差分隐私外,还提出了individual fairness的定义,与差分隐私定义类似,“相似的人应该被分类器相似地对待”, d d d为距离度量:
P ( Y ^ = y ∣ X ) ≈ P ( Y ^ = y ∣ X ′ ) , i f d ( X , X ′ ) ≈ 0 P(\hat{Y}=y|X)\approx P(\hat{Y}=y|X^{\prime}), \; if \; d(X,X^{\prime}) \approx0 P(Y^=y∣X)≈P(Y^=y∣X′),ifd(X,X′)≈0
什么是相似,多相似才是相似,是后来的工作主要研究点。
三、group fairness
相比于individual fairness相似性的难以描述,group fairness比较直白。group fairness考虑的场景是,样本依照敏感属性 Z Z Z分组, Y ∈ { − 1 , 1 } , Z ∈ { − 1 , 1 } Y\in \{-1,1\},Z\in \{-1,1\} Y∈{−1,1},Z∈{−1,1},预测结果 Y ^ = 1 \hat{Y}=1 Y^=1被认为是优势, Z = 1 Z=1 Z=1的组被认为是优势组别(容易被预测为 Y ^ = 1 \hat{Y}=1 Y^=1), Z = 0 Z=0 Z=0的组别被认为是劣势组别。
1. disparate impact
disparate impace(DI)是一个比值形式的定义,一般认为该值大于0.8,表示分类器是比较公平的。
D I = P ( Y ^ = 1 ∣ Z = − 1 ) P ( Y ^ = 1 ∣ Z = 1 ) ≥ 0.8 DI=\frac{P(\hat{Y}=1|Z=-1)}{P(\hat{Y}=1|Z=1)}\geq0.8 DI=P(Y^=1∣Z=1)P(Y^=1∣Z=−1)≥0.8
除此之外,也有工作将二者的差值定义为demographic parity,若较小,则分类器比较公平。这个指标的缺陷是,强制满足该指标,会让 Z = − 1 Z=-1 Z=−1的群体预测为 Y ^ = 1 \hat{Y}=1 Y^=1的概率大致相同,但是可能存在有的群体本身 P ( Y ^ = 1 ) P(\hat{Y}=1) P(Y^=1)非常低,满足该指标是对 Z = 1 Z=1 Z=1的群体的歧视。
D P = ∣ P ( Y ^ = 1 ∣ Z = − 1 ) − P ( Y ^ = 1 ∣ Z = 1 ) ∣ DP = |P(\hat{Y}=1|Z=-1) - P(\hat{Y}=1|Z=1)| DP=∣P(Y^=1∣Z=−1)−P(Y^=1∣Z=1)∣
2. predictive equality
如果分类器满足下式,则认为其满足predictive equality:
P ( Y ^ = 1 ∣ Y = − 1 , Z = − 1 ) = P ( Y ^ = 1 ∣ Y = − 1 , Z = 1 ) P(\hat{Y}=1|Y=-1, Z=-1) = P(\hat{Y}=1|Y = -1, Z=1) P(Y^=1∣Y=−1,Z=−1)=P(Y^=1∣Y=−1,Z=1)
3. equal opportunity
如果分类器满足下式,则认为其满足equal opportunity:
P ( Y ^ = 1 ∣ Y = 1 , Z = − 1 ) = P ( Y ^ = 1 ∣ Y = 1 , Z = 1 ) P(\hat{Y}=1|Y=1, Z=-1) = P(\hat{Y}=1|Y = 1, Z=1) P(Y^=1∣Y=1,Z=−1)=P(Y^=1∣Y=1,Z=1)
除此之外,也有工作将predictive equality和equal opportunity相交定义equalized odds,equalized odds越大,分类器越不公平:
E O D = ∑ y ∈ { − 1 , 1 } ∣ P ( Y ^ = 1 ∣ Y = y , Z = − 1 ) − P ( Y ^ = 1 ∣ Y = y , Z = 1 ) ∣ , EOD = \sum_{y \in\{-1,1\}}|P(\hat{Y}=1|Y=y, Z=-1) - P(\hat{Y}=1|Y = y, Z=1)|, EOD=y∈{−1,1}∑∣P(Y^=1∣Y=y,Z=−1)−P(Y^=1∣Y=y,Z=1)∣,
4. disparate mistreatment
侧重于不同群体上错误率相同,包括相同的FPR、FNR等:
o v e r a l l m i s c l a s s i f i c a t i o n r a t e ( O M R ) : overall \;misclassification \;rate(OMR): overallmisclassificationrate(OMR):
P ( Y ^ ≠ Y ∣ Z = − 1 ) = P ( Y ^ ≠ Y ∣ Z = 1 ) P(\hat{Y}\neq Y|Z=-1)=P(\hat{Y}\neq Y|Z=1) P(Y^=Y∣Z=−1)=P(Y^=Y∣Z=1)
f a l s e p o s i t i v e r a t e ( F P R ) : false\;positive \;rate(FPR): falsepositiverate(FPR):
P ( Y ^ ≠ Y ∣ Y = − 1 , Z = − 1 ) = P ( Y ^ ≠ Y ∣ Y = − 1 , Z = 1 ) P(\hat{Y}\neq Y|Y=-1,Z=-1)=P(\hat{Y}\neq Y|Y=-1,Z=1) P(Y^=Y∣Y=−1,Z=−1)=P(Y^=Y∣Y=−1,Z=1)
f a l s e n e g t i v e r a t e ( F N R ) : false\;negtive\;rate(FNR): falsenegtiverate(FNR):
P ( Y ^ ≠ Y ∣ Y = 1 , Z = − 1 ) = P ( Y ^ ≠ Y ∣ Y = 1 , Z = 1 ) P(\hat{Y}\neq Y|Y=1,Z=-1)=P(\hat{Y}\neq Y|Y=1,Z=1) P(Y^=Y∣Y=1,Z=−1)=P(Y^=Y∣Y=1,Z=1)
f a l s e o m i s s i o n r a t e ( F O R ) : false\;omission\;rate(FOR): falseomissionrate(FOR):
P ( Y ^ ≠ Y ∣ Y ^ = − 1 , Z = − 1 ) = P ( Y ^ ≠ Y ∣ Y ^ = − 1 , Z = 1 ) P(\hat{Y}\neq Y|\hat{Y}=-1,Z=-1)=P(\hat{Y}\neq Y|\hat{Y}=-1,Z=1) P(Y^=Y∣Y^=−1,Z=−1)=P(Y^=Y∣Y^=−1,Z=1)
f a l s e d i s c o v e r y r a t e ( F D R ) : false\;discovery\;rate(FDR): falsediscoveryrate(FDR):
P ( Y ^ ≠ Y ∣ Y ^ = 1 , Z = − 1 ) = P ( Y ^ ≠ Y ∣ Y ^ = 1 , Z = 1 ) P(\hat{Y}\neq Y|\hat{Y}=1,Z=-1)=P(\hat{Y}\neq Y|\hat{Y}=1,Z=1) P(Y^=Y∣Y^=1,Z=−1)=P(Y^=Y∣Y^=1,Z=1)
5. Predictive parity
不同组拥有相同的Positive Predictive Value(真阳率):
P ( Y = 1 ∣ Y ^ = 1 , Z = − 1 ) = P ( Y = 1 ∣ Y ^ = − 1 , Z = 1 ) P(Y=1|\hat{Y}=1,Z=-1)=P(Y=1|\hat{Y}=-1,Z=1) P(Y=1∣Y^=1,Z=−1)=P(Y=1∣Y^=−1,Z=1)
四、causal fairness
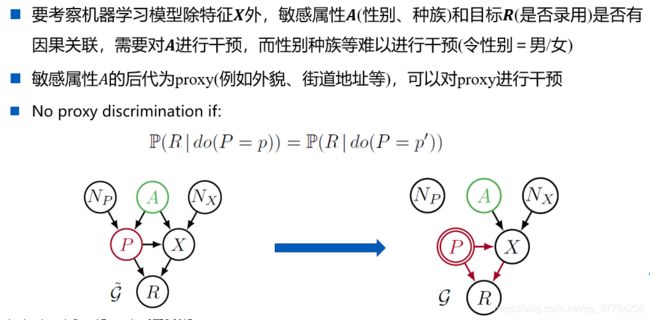
1. proxy discrimination
2. unresolved discrimination
3. conterfectual fairness
直接干预A的不足: 直接干预A,求取的是在A中的平均效应。如果群体中一半人被“正向”歧视,一半人被反向歧视,直接干预A不能发现这个问题
P ( Y ^ = 1 ∣ d o ( A = a ) ) = P ( Y ^ = 1 ∣ d o ( A = a ′ ) ) P(\hat{Y}=1|do(A=a))=P(\hat{Y}=1|do(A=a^{\prime})) P(Y^=1∣do(A=a))=P(Y^=1∣do(A=a′))
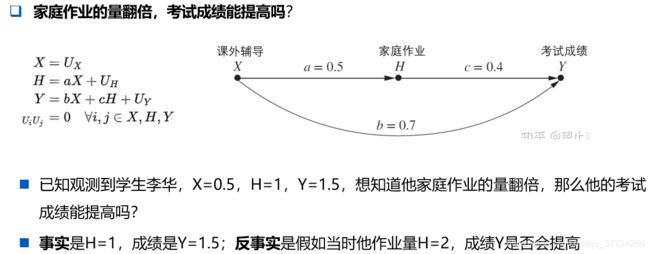
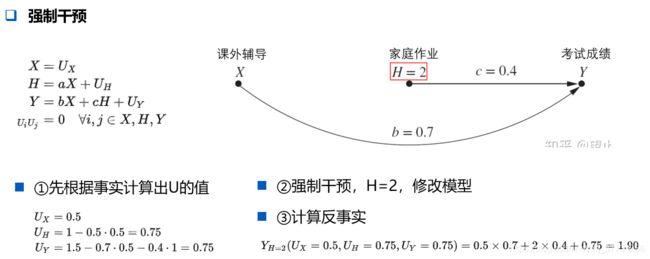
因而有人提出反事实公平性,反事实的直观表达是,在某件事情已经发生的情况下,假如当时XXX,这件事情还会是这个结果吗?例如下面的例子,来自《Causal Inference in Statistics:A Primer》,摘自知乎用户望止洋。先通过事实计算出模型的参数,接着强制干预,计算出反事实。
反事实公平性:
P ( Y ^ z = y ∣ X = x ) = P ( Y ^ z ′ = y ∣ X = x ) ∀ y , z , z ′ P(\hat{Y}_z=y|X=x)=P(\hat{Y}_{z^{\prime}}=y|X=x) \;\; \forall y,z,z^{\prime} P(Y^z=y∣X=x)=P(Y^z′=y∣X=x)∀y,z,z′
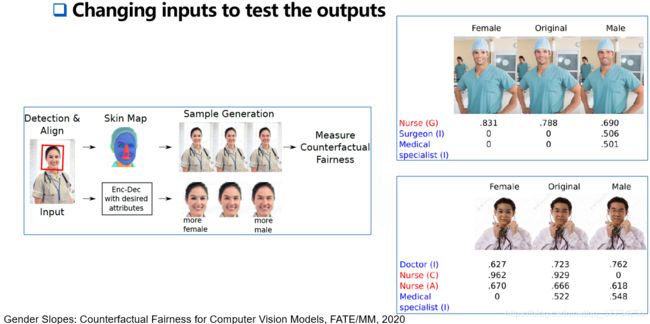
反事实公平性的直观上理解,比如同一个人,只改变一下性别,看看分类器的输出结果有没有改变很多,若改变了很多,则不满足反事实公平性
一些参考文献
[1] Fairness-Aware Machine Learning——An Extensive Overview, Jannik Dunkelau and Michael Leuschel
[2] Joon Sik Kim, Jiahao Chen, Ameet Talwalkar: FACT: A Diagnostic for Group Fairness Trade-offs. ICML 2020: 5264-5274
[3] Niki Kilbertus, Mateo Rojas-Carulla, Giambattista Parascandolo, Moritz Hardt, Dominik Janzing, Bernhard Schölkopf: Avoiding Discrimination through Causal Reasoning. NIPS 2017: 656-666
(未完待续&期待大佬们指出错误)