深蓝-视觉slam-第四节习题
#include CMakeLists.txt
cmake_minimum_required(VERSION 3.6)
find_package(OpenCV REQUIRED)
include_directories(${OpenCV_INCLUDE_DIRS})
add_executable(undistort_image undistort_image.cpp)
target_link_libraries(undistort_image ${OpenCV_LIBS})
实现效果:

2,鱼眼模型与去畸变


(1)与针孔相机原理不同, 鱼眼相机采用非相似成像,在成像过程中引入畸变,通过对直径空间的压缩,突破成像视角的局限,从而达到广角成像。鱼眼相机具有更宽的视场,因此在相同的传感器区域中包含了更多的信息,这个对物体检测,视觉里程计和3D见图尤为有利。
(2)在OpenCV中,鱼眼相机是采用等距模型进行标定的。畸变类型也不是简单的由上述的径向畸变和切向畸变描述的。
(3)实现代码:
#include CMakeLists.txt:
cmake_minimum_required(VERSION 3.16.3)
project(FISHE)
find_package(OpenCV 3.4.12 REQUIRED)
add_executable(fisheye fisheye.cpp)
target_link_libraries(fisheye ${OpenCV_LIBS})
实现效果:

(4)参考:https://blog.csdn.net/Gavinv/article/details/78386465?spm=1001.2014.3001.5502
由opencv官网给出的鱼眼相机模型为 θ d = θ ( k 1 θ 2 + k 2 θ 4 + k 3 θ 6 + k 4 θ 8 ) \theta_d = \theta (k_1 \theta^2 + k_2 \theta^4 + k_3 \theta^6 + k_4 \theta^8) θd=θ(k1θ2+k2θ4+k3θ6+k4θ8)等距投影函数 : r = f θ r = f \theta r=fθ 通过泰勒公式展开,由于畸变参数 k 1 , k 2 , k 3 , k 4 k_1, k_2,k_3,k_4 k1,k2,k3,k4都等与0,只保留 θ \theta θ一次项,相当于畸变系数 k 0 = 1 k_0 = 1 k0=1, 仍然含有畸变参数,所以即使 k 1 , k 2 , k 3 , k 4 k_1, k_2,k_3,k_4 k1,k2,k3,k4 都为0,仍可以对畸变图进行校正。
(5)去畸变虽然解决了鱼眼相机的3D建图问题,但同时由校正后的图像可以看出也消除了鱼眼相机的主要优点,靠近图像边缘的信息高度失真,而靠近中心的对象被高度压缩。
在原有畸变校正公式中加入了尺度因子。首先,基于尺度因子建立新的图 像矩阵,因为畸变校正导致的边缘损失范围较小,因此尺度因子选为2可以满足大多数情况 要求,新建立的图像矩阵除左上角四分之一面积为源图像像素值,其他范围为全零矩阵,新 图像长宽为原始图像的2倍;然后将待校正图像平移至新图像中心区域,然后进行图像径向 畸变校正,校正完毕后获取图像中四个角点像素位置,提取矩形区域作为校正后的图像。这 样获取的校正后图像的完整信息都得到保留,但是会引入边缘的零像素区域,由于相邻相 机拍摄区域具有重叠部分,因此零像素区域可以通过重叠区域融合模块去除,最终实现在 无边缘损失的情况下的图像校正功能。
3,双目视差的使用

1.1 已知像素u,v,d求空间点坐标
x,y是相机坐标下的归一化平面上的坐标,此时的z = 1 , b 表示基线,d代表视差
x = (u - cx) / fx, y = (v - cy) / fy; z = fx * b / d;
由此可得,相机模型下三维点的坐标X,Y,Z为X = x * z; Y = y * z; Z = z;
1.2 已知相机模型下相机坐标的X,Y,Z求u,v,d
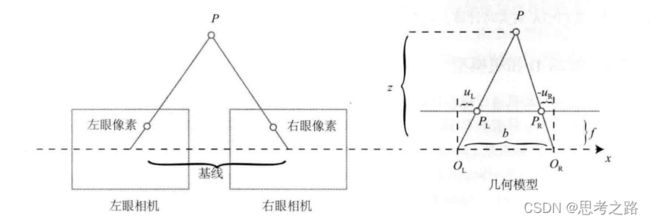
由三角形相似关系可以得到:(Z - f) / Z = (b - uL +uR) / b,在 整理可得到Z = (f - b) / (uL - uR),整理得到 视差d = uL - uR;
(X/Z , Y/Z ,Z/Z),为归一化平面上的点,然后乘以相机的内参就可以得到对应的像素坐标u,v
u = fx * X/Z + cx , v = fy * Y/z + cy;
题外知识:单目相机成像原理:
- 世界坐标系下有一个点P,世界坐标系为Pw.
- 由于相机在运动,它的运动由R,t或变换矩阵T描述。P的相机坐标为RPw + t;
- 这时Pc的分量为X,Y,Z,把他们投影到归一化平面上得到归一化坐标:Pc = [ X / Z , Y / Z , 1 ] T [X/Z, Y/Z, 1]^T [X/Z,Y/Z,1]T;
- 有畸变时,根据畸变参数计算Pc发生畸变后的坐标;
- P的归一化坐标经过内参后,对应它的像素坐标为:Puv = KPc;
我们谈到了四种坐标:世界坐标,相机坐标,归一化坐标和像素坐标。
Z P u v = Z [ u v 1 ] = K ( R P w + t ) = K T P w (1 ) ZP_{uv}= Z \left[\begin{matrix}u\\v \\1\end{matrix}\right] = K(RP_w + t) = KTP_w\tag{1 } ZPuv=Z⎣⎡uv1⎦⎤=K(RPw+t)=KTPw(1 )
[ u v 1 ] = 1 Z [ f x 0 c x 0 f y c y 0 0 1 ] [ X Y Z ] (2) \left[ \begin{matrix} u \\ v \\ 1 \end{matrix} \right] = \frac{1}{Z}\left[ \begin{matrix} f_x & 0 & c_x \\ 0 & f_y & c_y\\ 0 & 0 & 1 \end{matrix} \right] \left[ \begin{matrix} X\\ Y \\ Z \end{matrix} \right] \tag{2} ⎣⎡uv1⎦⎤=Z1⎣⎡fx000fy0cxcy1⎦⎤⎣⎡XYZ⎦⎤(2)
2.1 推导在右目模型下该模型的变化
左右眼的相机内参是相同的。在右眼模型下,世界坐标系下的点Pw,在左眼相机坐标系下的坐标为RPw + t, 而左眼和右眼的相机坐标系只是发生了平移,即右眼坐标系下的坐标为PRw + t + b(基线),然后把该相机下的坐标在归一化平面表示,然后利用内参将其转为像素坐标即可。
3 编程
3.1 编程部分代码
#include (v, u) <= 10.0 || disparity.at(v, u) >= 96.0) {
// continue;
// }
Vector4d point(0, 0, 0, left.at<uchar>(v, u) / 255.0); // 前三维为xyz,第四维为颜色
// 根据双目模型计算 point 的位置
double x = (u - cx) / fx;
double y = (v - cy) / fy;
double depth = fx * d / (disparity.at<char>(v, u));
point[0] = x * depth;
point[1] = y * depth;
point[2] = depth;
pointcloud.push_back(point);
}
cv::imshow("disparity", disparity);
cv::waitKey(0);
// 画出点云
showPointCloud(pointcloud);
return 0;
}
void showPointCloud(const vector<Vector4d, Eigen::aligned_allocator<Vector4d>> &pointcloud) {
if (pointcloud.empty()) {
cerr << "Point cloud is empty!" << endl;
return;
}
pangolin::CreateWindowAndBind("Point Cloud Viewer", 1024, 768);
glEnable(GL_DEPTH_TEST);
glEnable(GL_BLEND);
glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);
pangolin::OpenGlRenderState s_cam(
pangolin::ProjectionMatrix(1024, 768, 500, 500, 512, 389, 0.1, 1000),
pangolin::ModelViewLookAt(0, -0.1, -1.8, 0, 0, 0, 0.0, -1.0, 0.0)
);
pangolin::View &d_cam = pangolin::CreateDisplay()
.SetBounds(0.0, 1.0, pangolin::Attach::Pix(175), 1.0, -1024.0f / 768.0f)
.SetHandler(new pangolin::Handler3D(s_cam));
while (pangolin::ShouldQuit() == false) {
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT); //清空颜色和深度缓
d_cam.Activate(s_cam);//激活显示,并设置相机的状态
glClearColor(1.0f, 1.0f, 1.0f, 1.0f); //设置背景颜色为白色
glPointSize(2);
glBegin(GL_POINTS);
for (auto &p: pointcloud) {
glColor3f(p[3], p[3], p[3]);
glVertex3d(p[0], p[1], p[2]);
}
glEnd();
pangolin::FinishFrame();
usleep(5000); // sleep 5 ms
}
return;
}
3.2 CMakeLists.txt
cmake_minimum_required(VERSION 3.6)
find_package(Pangolin REQUIRED)
find_package(OpenCV REQUIRED)
include_directories(${Pangolin_INCLUDE_DIRS})
include_directories(${OpenCV_INCLUDE_DIRS})
include_directories("/usr/include/Eigen")
add_executable(right-left disparity.cpp)
target_link_libraries(right-left ${OpenCV_LIBS} ${Pangolin_LIBRARIES} ${Eigen_LIBRARIES})
3.3 实现效果
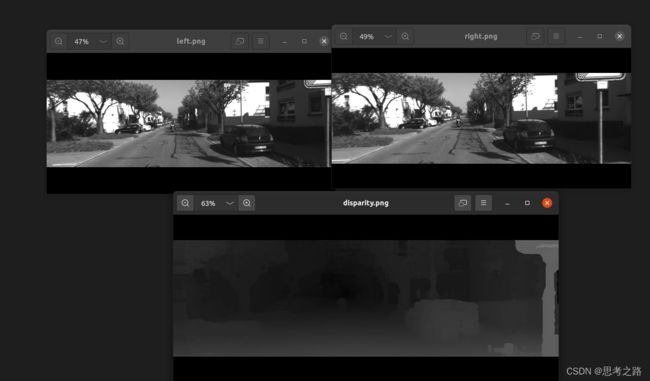

4,矩阵运算微分

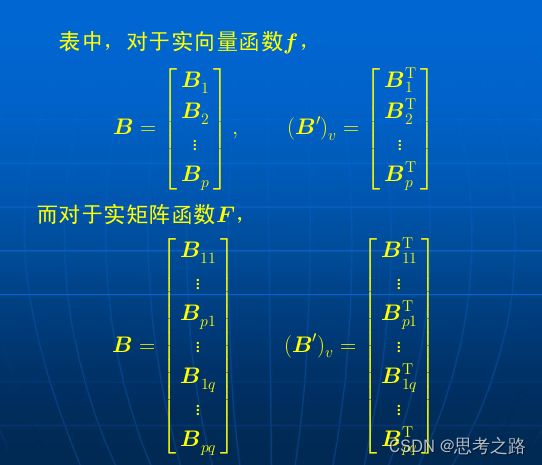
(1) d ( A x ) d x = A T \frac{d(Ax)}{d_x} = A^T dxd(Ax)=AT
(2)

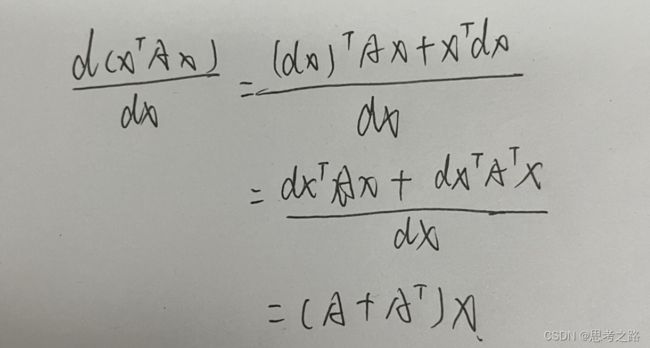
(3)
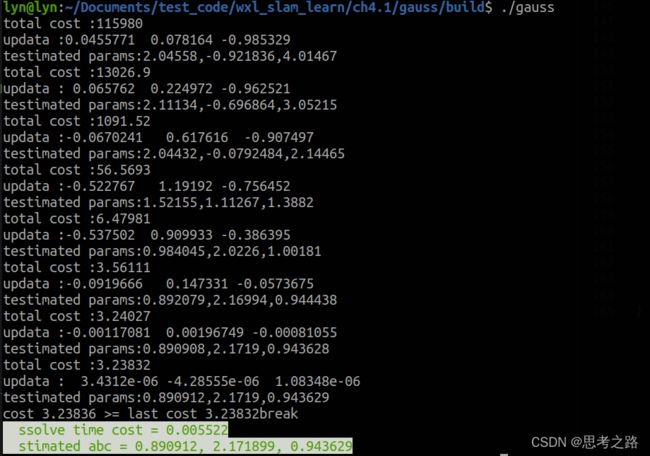
5,高斯牛顿法的曲线拟合实验

程序代码:
#include CMakeLists.txt
cmake_minimum_required(VERSION 3.6)
find_package(OpenCV REQUIRED)
include_directories(${OpenCV_INCLUDE_DIRS})
add_executable(gauss gaussnewton.cpp)
target_link_libraries(gauss ${OpenCV_LIBS})