残差网络ResNet
文章目录
-
- ResNet模型
- 两个注意点
-
- 关于x
- 关于残差单元
- 核心实验
-
- 原因分析
- ResNet的效果
- 题外话
ResNet是由何凯明在论文Deep Residual Learning for Image Recognition里提出的
论文链接:https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=7780459
ResNet模型
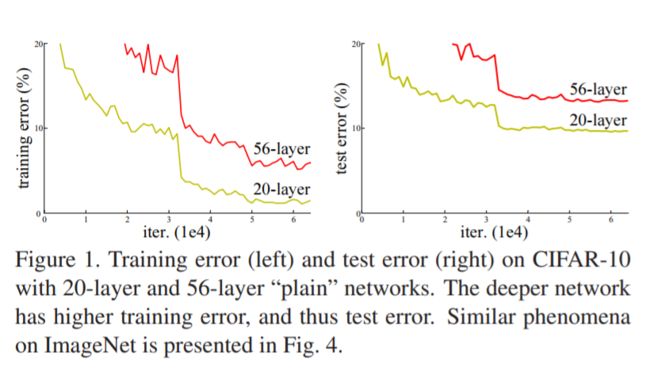
如上图,网络深度增加时,56层的网络比20层网络效果还要差。这不会是过拟合问题,因为56层网络的训练误差同样高(具体分析见最后实验)。如何解决这个问题呢?
我们考虑一个极端情况,现在有一个浅层网络,你如果深层什么也不学仅复制浅层网络的特征,在这种情况下,深层和浅层网络性能一样,就不会出现退化现象。基于这种假设,设计出了ResNet:
本来应该学习特征 H ( x ) H(x) H(x),这里拆分成残差和x的和,也就是 H ( x ) = F ( x ) + x H(x)=F(x)+x H(x)=F(x)+x, x x x相当于一个短连接直接到输出,所以只学习残差 F ( x ) F(x) F(x)即可。
y l = x l + F ( x l , W l ) x l + 1 = f ( y l ) \begin{array}{l} y_{l}=x_{l}+F\left(x_{l}, W_{l}\right) \\ x_{l+1}=f\left(y_{l}\right) \end{array} yl=xl+F(xl,Wl)xl+1=f(yl)
x l x_l xl和 x l + 1 x_{l+1} xl+1分别表示第 l l l和 l + 1 l+1 l+1层的输入, F F F是残差函数(注意每个残差单元一般是多层), f f f是ReLU激活函数。上面的式子不断迭代,得到从浅层 l l l到深层 L L L的学习特征为:
x L = x l + ∑ i = l L − 1 F ( x i , w i ) (1) x_{L}=x_{l}+\sum_{i=l}^{L-1} F\left(x_{i}, w_{i}\right) \tag{1} xL=xl+i=l∑L−1F(xi,wi)(1)
对于任何深度的L来讲,公式1显示了一些良好的特性:
- 第 L L L层的特征 x L x_L xL可以分为两个部分,浅层网络表示 x l x_l xl加上一个残差函数映射,表明模型在任意单元内都是一个残差的形式
- 对于任意深度 L L L层的特征 x L x_L xL来说,它是前面所有残差模块的和,这与简单的不加短连接的网络完全相反(不加短连接的网络是一系列向量乘的结果)
在反向传播时效果也很好,利用链式法则,带入(1)式得:
∂ l o s s ∂ x l = ∂ l o s s ∂ x L ∂ x L ∂ x l = ∂ l o s s ∂ x L ( 1 + ∂ ∂ x l ∑ i = l L − 1 F ( x i , w i ) ) (2) \frac{\partial {loss}}{\partial x_{l}}=\frac{\partial {loss}}{\partial x_{L}} \frac{\partial x_{L}}{\partial x_{l}}=\frac{\partial {loss}}{\partial x_{L}}\left(1+\frac{\partial}{\partial x_{l}} \sum_{i=l}^{L-1} F\left(x_{i}, w_{i}\right)\right) \tag{2} ∂xl∂loss=∂xL∂loss∂xl∂xL=∂xL∂loss(1+∂xl∂i=l∑L−1F(xi,wi))(2)
其中, ∂ l o s s ∂ x L \frac{\partial {loss}}{\partial x_{L}} ∂xL∂loss表示损失函数到达 L L L的梯度,括号内,1表明短路机制可以无损地传播梯度, ∂ ∂ x l ∑ i = l L − 1 F ( x i , w i ) \frac{\partial}{\partial x_{l}} \sum_{i=l}^{L-1} F\left(x_{i}, w_{i}\right) ∂xl∂∑i=lL−1F(xi,wi)表示梯度要经过weights加权层,两部分连接的线形特性保证了信息可以直接反向传播到浅层。残差梯度不会那么巧全为-1,所以有1的存在保证不会导致梯度消失。
要注意上面的推导并不是严格的证明。
两个注意点
关于x
因为 F + x F+x F+x是element-wise相加,那么如果二者维度不一样怎么办?
-
策略一:直接对 x x x补0
-
策略二:增加一个网络层,进行新的映射,改变 x x x的维度(但是策略二会增加参数和计算量,故不是必须的)
y = F ( x , { W i } ) + W s x y=F\left(x,\left\{W_{i}\right\}\right)+W_{s} x y=F(x,{Wi})+Wsx
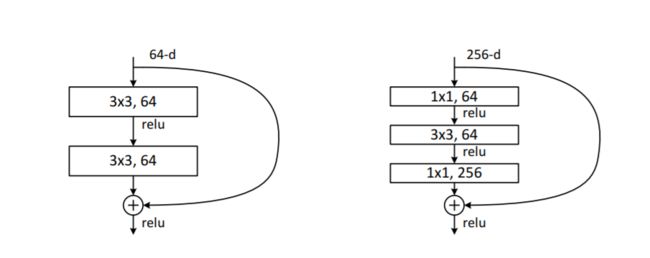
关于残差单元
可以是2层或者3层,也可以是更多;但是不要是1层,效果会不好。(训练更深层的网络时,用右图代替左图的)
核心实验

如图,左边是plain network,右边是ResNet;细线是train error,加粗线是val error
原因分析
Plain network会出现网络的层数增加,train error和val error都会升高,为什么?
- 首先排除过拟合,因为train error也会升高
- 其次排除梯度消失,网络中使用了batch normalization,并且作者也做实验验证了梯度的存在(34-layers plain network也是可以实现比较好的准确率的,这说明网络在一定程度上也是work了的)
作者猜测,是因为层数的提升会在一定程度上指数级别影响收敛速度。
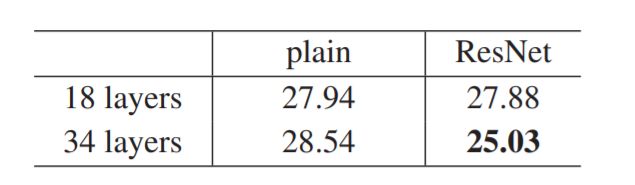
ResNet的效果
通过上面两张图,ResNet在不增加任何参数的情况下,仅使用shortcuts and zero-padding for matching dimensions结构,就一定程度上解决了网络的退化问题,并实现了更高的准确率,更快的收敛速度!
题外话
深度残差网络(Deep residual network, ResNet)的提出是CNN发展的一件里程碑事件,是由何凯明提出的,并因此摘得CVPR2016最佳论文奖。大家有时间可以看一下他的辉煌战绩:

参考文章:
重读经典:完全解析特征学习大杀器ResNet
你必须要知道CNN模型:ResNet
一文读懂残差网络ResNet