前言
本文只讨论二维三维中的permute用法
最近的Attention学习中的一个permute函数让我不理解
这个光说太抽象
我就结合代码与图片解释一下
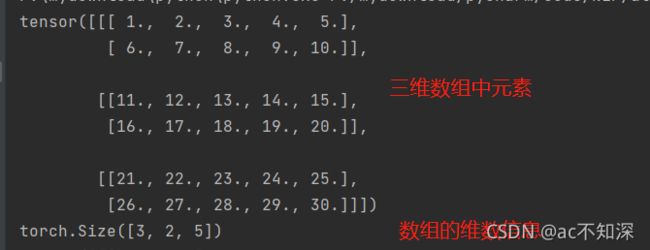
首先创建一个三维数组小实例
import torch x = torch.linspace(1, 30, steps=30).view(3,2,5) # 设置一个三维数组 print(x) print(x.size()) # 查看数组的维数
这里为了防止出现维数数值相同的巧合局面(例如三维数组(3,3,3)或者(2,4,4)等)
输出结果如下图
一般的把(3,2,5)解释为3维2行5列这里很容易让人迷迷糊糊
那么我们按照块,行,列理解起来会更容易一些
比如(3,2,5),表示3块 2*5的数组
以下我简单用3块3*3图偷懒举例
然后堆起来就是我们熟知的三维矩阵
接下来先简单介绍下permute()函数
permute(dims)
参数dims用矩阵的维数代入,一般默认从0开始。即第0维,第1维等等
也可以理解为,第0块,第1块等等。当然矩阵最少是两维才能使用permute
如是两维,dims分别为是0和1
可以写成permute(0,1)这里不做任何变化,维数与之前相同
如果写成permute(1,0)得到的就是矩阵的转置
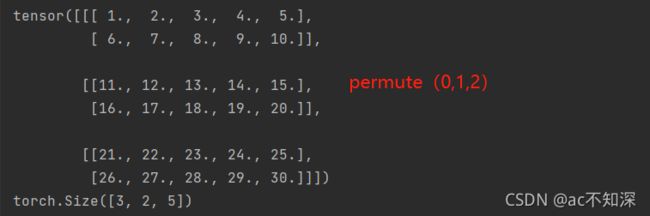
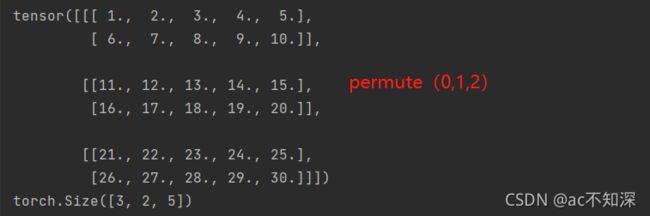
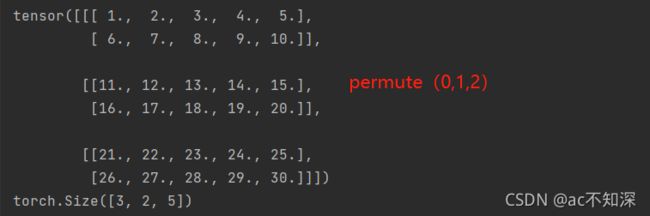
如果三维是permute(0,1,2)
0代表共有几块维度:本例中0对应着3块矩阵
1代表每一块中有多少行:本例中1对应着每块有2行
2代表每一块中有多少列:本例中2对应着每块有5列
所以是3块2行5列的三维矩阵
这些0,1,2并没有任何实际的意义,也不是数值,只是用来标识区别。有点类似于x,y,z来区分三个坐标维度,是人为规定好的
三维情况直接用下面的代码来给大家讲解
三维情况
变化一:不改变任何参数
b = x.permute(0,1,2) # 不改变维度 print(b) print(b.size())
发现此时矩阵没有变化,依然是按照之前的方式排列
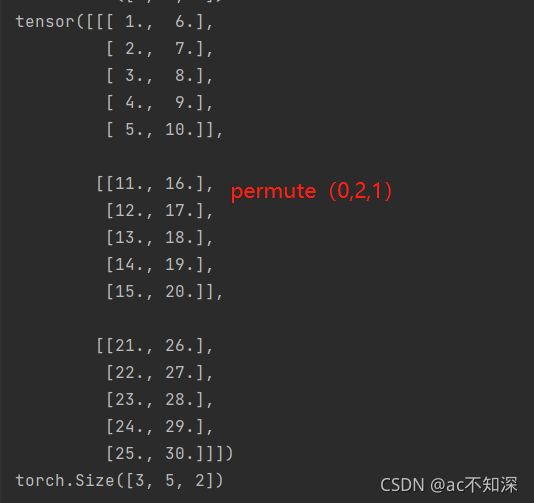
变化二:1与2交换
b = x.permute(0,2,1) # 每一块的行与列进行交换,即每一块做转置行为 print(b) print(b.size())
两张图片可以比较
在不改变每一块(即)的前提下,对每一块的行列进行对调(即二维矩阵的转置)
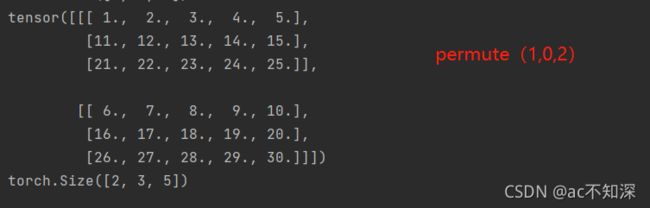
变化三:0与1交换
b = x.permute(1,0,2) # 交换块和行 print(b) print(b.size())
两者比较可以看出块数和每块的行数发生了变化
即参数0对应的数值3块变成2块
参数1对应的2行变成3行
这个变化刚好是0与1 的位置交换,导致参数进行对调
此时变成了2块 * 3行 * 5列(初始为3块 * 2行 *5列)
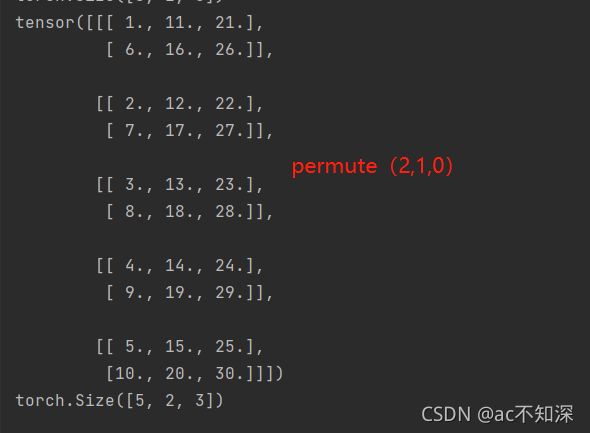
变化四:0与2交换
b = x.permute(2,1,0) # 交换块和列 print(b) print(b.size())
此时参数0对应的3块经过permute已经变成了5块
参数2对应的5列已经变成了3列
变化五:0与1交换,1与2交换
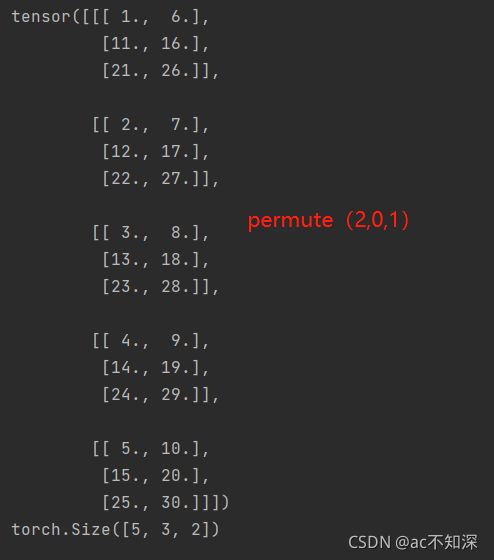
b = x.permute(2,0,1) # 交换块和行和列 print(b) print(b.size())
此时参数0对应的3块变成了5块
参数1对应的2行变成了3行
参数2对应的5列变成了2列
变化六:0与1交换,0与2交换
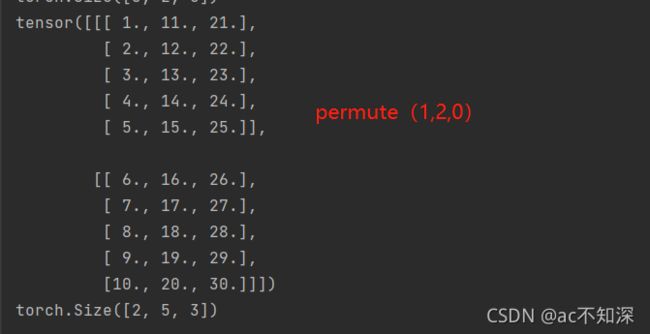
b = x.permute(1,2,0) # 交换块和行和列 print(b) print(b.size())
此时参数0对应的3块变成了2块
参数1对应的2行变成了5行
参数2对应的5列变成了3列
总结
根据以上举得二维和三维例子可以知道permute()函数其实是对矩阵的块行列进行交换
里面的参数并不是具体数值
而是块行列的代指
写在最后
没想随手写的一篇居然这么多读者关注
我又在此篇文章的基础上,详细的解释了维度变化过程
能够更好的帮助大家理解permute函数的用法
进阶文章请戳我
到此这篇关于pytorch中permute()函数用法的文章就介绍到这了,更多相关pytorch permute()函数用法内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家!