LeetCode209——长度最小的子数组

我的LeetCode代码仓：https://github.com/617076674/LeetCode

原题链接：https://leetcode-cn.com/problems/minimum-size-subarray-sum/description/

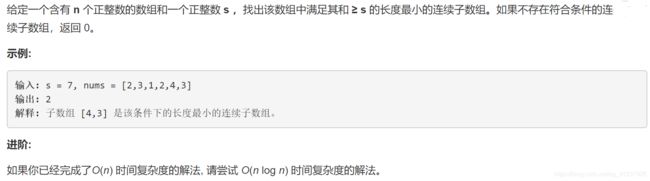
题目描述：

知识点：滑动窗口法

思路一：从左到右遍历数组寻找最小长度

时间复杂度是O(n ^ 2)，其中n为nums数组的长度。空间复杂度是O(1)。

JAVA代码：

public class Solution {
    public int minSubArrayLen(int s, int[] nums) {
        int result = Integer.MAX_VALUE;
        boolean flag = false;
        for(int i = 0; i < nums.length; i++){
            int sum = 0;
            for(int j = i; j < i + result && j < nums.length; j++){
                sum += nums[j];
                if(sum >= s){
                    result = Math.min(result, j - i + 1);
                    flag = true;
                    break;
                }
            }
        }
        if(!flag){
            return 0;
        }
        return result;
    }
}

LeetCode解题报告：

思路二：滑动窗口法

注意到题目限定的条件：该数组中的元素均是正整数。因此我们可以用滑动窗口法来解决，当和小于s时，滑动窗口右端点向右移动，使窗口增大；当和大于s时，滑动窗口左端点向右移动，使窗口缩小。

时间复杂度是O(n)，其中n为nums数组的长度。空间复杂度是O(1)。

JAVA代码：

public class Solution {
    public int minSubArrayLen(int s, int[] nums) {
        int left = 0;
        int right = -1;			//把[left, right]区间看作是一个滑动窗口，初始时滑动窗口中没有元素故right = -1
        int sum = 0;
        int len = nums.length + 1;		//n + 1比整个数组的长度还大，但要注意这个值其实是取不到的
        while(left < nums.length) {
            if(right + 1 < nums.length && sum < s) {		//当sum < s时，滑动窗口向右延伸使窗口内的值变大
                right++;
                sum += nums[right];
            }else {								//当sum >= s时，滑动窗口left增大，使窗口向右缩进使得窗口内的值变小
                sum -= nums[left];
                left++;
            }
            if(sum >= s) {
                len = Math.min(len, right - left + 1);
            }
        }
        if(len == nums.length + 1) {
            return 0;
        }else {
            return len;
        }
    }
}

LeetCode解题报告：

思路三：二分查找法

先根据nums数组求得其和数组sums，其中sums[0] = 0, sums[1] = nums[0], sums[2] = nums[0] + nums[1], ...

由于nums数组中的元素都是正整数，故sums数组一定是一个递增的数组，我们在sums数组中查找一个值时，可以使用二分查找法。

对sums数组中的每个位置，二分查找其另一端点s + sums[i - 1]。

时间复杂度是O(nlogn)，其中n为nums数组的长度。空间复杂度是O(logn)。

JAVA代码：

public class Solution {
    public int minSubArrayLen(int s, int[] nums) {
        if(0 == nums.length){
            return 0;
        }
        int result = Integer.MAX_VALUE;
        int[] sums = new int[nums.length + 1];
        for(int i = 1; i < sums.length; i++){
            sums[i] = sums[i - 1] + nums[i - 1];
        }
        for(int i = 1; i < sums.length; i++){
            int temp = lowerBound(sums, 0, sums.length - 1, s + sums[i - 1]);
            if(-1 != temp){
                result = Math.min(result, temp - i + 1);
            }
        }
        if(result == Integer.MAX_VALUE){
            return 0;
        }
        return result;
    }
    private int lowerBound(int[] nums, int left, int right, int target){
        if(left > right){
            return -1;
        }
        if(left == right){
            return nums[left] >= target ? left : -1;
        }
        int mid = left + (right - left) / 2;
        if(nums[mid] >= target){
            return lowerBound(nums, left, mid, target);
        }else{
            return lowerBound(nums, mid + 1, right, target);
        }
    }
}

LeetCode解题报告：