原文链接:http://tecdat.cn/?p=26632
理解世界,我们可以从相关性的角度去描述,统计,机器学习,很多问题都是从相关的角度去描述的。我们去构建一个模型,不管是统计机器学习模型,还是深度学习模型,本质上是构建一个复杂映射。从特征到标签的一个映射,这个映射是有用的,但不完全有用。
因果分析
我们在这里用一个隐喻,下雨,来描述causal 和relevance。我们可以构建一个关于预测明天是否下雨的模型,从搜集到的大量特征,以及历史的下雨结果最为标签,构建模型。不管准确率多少,我们用这样一个模型能够预测明天是否能够下雨。
但是,我们很多时候要的不仅仅是预测,而是需要改变现状,例如沙漠中,我们想要哪些因素改变了,能够导致下雨。这就涉及到因果推断, causal inference 。
因果生存分析
在报告随机实验的结果时,除了意向治疗效应外,研究人员通常选择呈现符合方案效应。然而,这些符合方案的影响通常是回顾性描述的,例如,比较在整个研究期间坚持其指定治疗策略的个体之间的结果。这种对符合方案效应的回顾性定义经常被混淆,并且无法进行因果解释,因为它遇到了治疗混杂因素。
我们的目标是概述使用逆概率加权对生存结果的因果推断。这里描述的基本概念也适用于其他类型的暴露策略,尽管这些可能需要额外的设计或分析考虑。
生存曲线的非参数估计
# 对数据进行一些预处理
ifelse(nes$death==0, 120,
(ns$yrh-83)*12+nhefs$moh) # yrt从83到92不等summary(survtime)survdiff(Surv(srtm, dah) ~ qmk, data=nes)fit <- survfit(Surv(rvie, dth) ~ sk, data=ns)
ggsurvplot(fit通过风险模型对生存曲线进行参数化估计
# 创建月数据
efsurv$ent <- ifelse(nhfs.rv$time==nhfs.urv$srvme-1 &
nhf.srv$death==1, 1, 0)
# 拟合参数性风险模型
haads.el <- glm(event==0 ~ qs#对每个人月的估计(1-风险)的分配 */
qk0$pnoevt0 <- predict(hardoel, mk0, type="response")
# 计算每个人月的生存率
qm0$uv0 <- cumprod(qm0$pnoet0)
# 一些数据管理来绘制估计的生存曲线
hadgrh$suvdff <- haardsgph$suv1-hardgrph$srv0
# 绘制
ggplot(hads.aph通过IP加权风险模型估计生存曲线
# 估计ip权重的分母
nef$p.mk <- predict(enm, nes, type="response")
# 估计ip权重的分子
p.m <- glm(qk ~ 1, data=nefs, family=binomial() )
hfs$pnsm <- predict(p.m, nes, type="response")
# 估计权重的计算
nef$s.<- ifelse(hes$qsk==1, nefs$pqmk/nhes$d.qmk,
(1-nfs$p.smk)/(1-nef$pdqk))
summary(nhs$swa)# 创建人月数据
nhfsw <- exnRos(nhfs, "srvtime", drop=F)
nh.pw$ime <- sqee(rle(nefs.ipw$seqn)$lengths)-1
nhfipw$evnt <- ifele(nhf.iw$tie=nhefs.i$rv1 &)
nhfs.w$eath==1, 1, 0)
nhefpw$tmesq <- nhfs.pw$me^2
# 拟合加权风险模型
imel <- glm(eve# 创建生存曲线
ipw.k0 <- data.frame(cbind(seq(0, 119),0, (seq(0, 119))^2))
# 对每个人月的估计(1-危险)的分配 */
iwqk0$p.nvnt0 <- predict(ipwdl, pwm0, type="response")
iwsk1$povt1 <- predict(ip.el, ipmk1, type="response")
# 计算每个人月的生存率
ip.qs0$srv0 <- cumprod(ipwsk0$p.nevnt0)
ip.qm1$suv1 <- cumprod(iwqsk1$p.nvent1)
# 一些数据管理来绘制估计的生存曲线
ipwgph <- merge(ip.qmk0,pwsm1, by=c("time", "timesq") )
ipw.aph$surff <-ipw.ah$sv1-pwgrph$surv0
# 绘制
ggplot(ip.gph, ae通过g-formula估计生存曲线
# 带有协变量的风险模型的拟合情况
g.mo <- glm(event==0 ~ qsm# 创建数据集,包括每个治疗水平下的所有时间点
# 每个人在每个治疗水平下的所有时间点
gf.qmk <- exanos(nfs, cunt=120, cotis.cl=F)
gf.qm0$te <- rep(q(0, 119), now(nhf))
gqm0$tesq <- gqk0$tie^2
gqsk0$qmk <- 0
gfqsk1 <- gf.qm0
gf.sk1$mk <- 1
gfqk0$p.vnt0 <- predict(g.mdel, g.qk0, type="response")
gfqk1$p.eent1 <- predict(gf.mol, gf.mk1, type="response")# 绘图
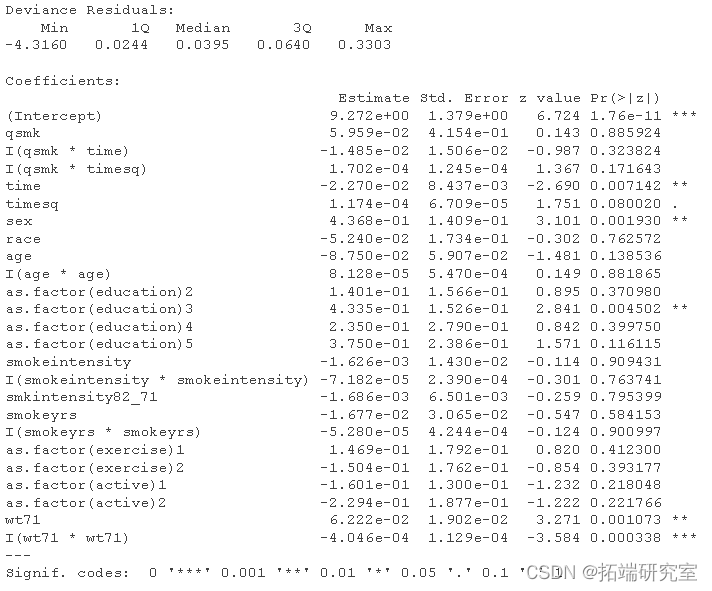
ggplot(gf.graph通过结构嵌套AFT模型估计中位生存时间比率
# 对数据进行一些预处理
#
modelA <- glm(qsmk ~ sex +
nhs$pqsk <- predict(moeA, nhe, type="response")
d <- nes\[!is.na(hf$surve),\] # 只选择有观察到的死亡时间的人
# 定义需要被最小化的估计函数
smf <- function(pi){
# 创建delta指标
if (psi>=0){
delta <- ifelse
1, 0)
} else if (psi < 0) {
dlta <- ifelse
}
# 协方差
sgma <- t(at) %*% smat
if (sa == 0){
siga <- 1e-16
}
etm <- svl\*solve(sia)\*t(sal)
return(etmeq)
}
res <- optimize
# 使用简单的分割法找到95%置信度下限和上限的估计值
frcf <- function(x){
return(smef(x) - 3.84)
}
if (bfuc < 3.84){
# 找到sumeef(x)>3.84的估计值
# 95%CI的下限
while (tetlw < 3.84 & cnlow < 100){
psl <- pilw - incre
teslow <- sumeef(pslw)
cunlow <- cunlow + 1
}
# 95%CI的上限值
while (tsigh < 3.84 & onhih < 100){
phigh <- pshih + inrem
testig <- sumeef(pihigh)
cunhgh <- cuntigh + 1
}
# 使用分切法进行更好的估计
if ((tstig > 3.84) & (tslw > 3.84)){
# 分割法
cont <- 0
dif <- right - left
while {
test <- fmiddle * fleft
if (test < 0){
} else {
}
diff <- right - left
}
psi_high <- middle
objfunc_high <- fmiddle + 3.84
# 95%CI的下限
left <- psilow
while(!){
test <- fmiddle * fleft
if (test < 0)最受欢迎的见解
3.R语言如何在生存分析与Cox回归中计算IDI,NRI指标