《Python数据分析基础教程:NumPy学习指南(第2版)》笔记14:第六章 深入学习NumPy模块2——随机数模块random
当前Numpy版本为:1.20
第六章 深入学习NumPy模块
6.13 快速傅里叶变换
FFT(Fast Fourier Transform,快速傅里叶变换)是一种高效的计算DFT(Discrete Fourier Transform,离散傅里叶变换)的算法。FFT算法比根据定义直接计算更快,计算复杂度为O(NlogN) 。DFT在信号处理、图像处理、求解偏微分方程等方面都有应用。在NumPy中,有一个名为fft的模块提供了快速傅里叶变换的功能。在这个模块中,许多函数都是成对存在的,也就是说许多函数存在对应的逆操作函数。例如,fft和ifft函数就是其中的一对。
6.14 动手实践:计算傅里叶变换
首先,我们将创建一个信号用于变换。计算傅里叶变换的步骤如下。
-
(1) 创建一个包含30个点的余弦波信号,如下所示:
import numpy as np x = np.linspace(0, 2 * np.pi, 30) wave = np.cos(x) -
(2) 使用
fft函数对余弦波信号进行傅里叶变换。transformed = np.fft.fft(wave) -
(3) 对变换后的结果应用
ifft函数,应该可以近似地还原初始信号。print( np.all(np.abs(np.fft.ifft(transformed) - wave) < 10 ** -9))结果如下:
True -
(4) 使用Matplotlib绘制变换后的信号。
import matplotlib.pyplot as plt plt.plot(transformed) plt.show()
案例完整代码如下:
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(0, 2 * np.pi, 30)
wave = np.cos(x)
transformed = np.fft.fft(wave)
print( np.all(np.abs(np.fft.ifft(transformed) - wave) < 10 ** -9))
plt.plot(transformed)
plt.show()
6.15 移频
numpy.linalg模块中的fftshift函数可以将FFT输出中的直流分量移动到频谱的中央。ifftshift函数则是其逆操作。
6.16 动手实践:移频
我们将创建一个信号用于变换,然后进行移频操作,步骤如下。
-
(1) 创建一个包含30个点的余弦波信号。
import numpy as np x = np.linspace(0, 2 * np.pi, 30) wave = np.cos(x) -
(2) 使用
fft函数对余弦波信号进行傅里叶变换。transformed = np.fft.fft(wave) -
(3) 使用
fftshift函数进行移频操作。shifted = np.fft.fftshift(transformed) -
(4) 用
ifftshift函数进行逆操作,这将还原移频操作前的信号。print( np.all(np.abs(np.fft.ifftshift(shifted) - transformed) < 10 ** -9))结果如下:
True -
(5) 使用Matplotlib分别绘制变换和移频处理后的信号。
import matplotlib.pyplot as plt plt.plot(transformed, lw=2) plt.plot(shifted, lw=3) plt.show()
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(0, 2 * np.pi, 30)
wave = np.cos(x)
transformed = np.fft.fft(wave)
shifted = np.fft.fftshift(transformed)
print( np.all(np.abs(np.fft.ifftshift(shifted) - transformed) < 10 ** -9))
plt.plot(transformed, lw=2)
plt.plot(shifted, lw=3)
plt.show()
6.17 随机数
随机数在蒙特卡罗方法(Monto Carlo method)、随机积分等很多方面都有应用。真随机数的产生很困难,因此在实际应用中我们通常使用伪随机数。在大部分应用场景下,伪随机数已经足够随机,当然一些特殊应用除外。有关随机数的函数可以在NumPy的random模块中找到。随机数发生器的核心算法基于马特赛特旋转演算法(Mersenne Twister algorithm)。随机数可以从离散分布或连续分布中产生。分布函数有一个可选的参数size,用于指定需要产生的随机数的数量。该参数允许设置为一个整数或元组,生成的随机数将填满指定形状的数组。支持的离散分布包括几何分布、超几何分布和二项分布等。
6.18 动手实践:硬币赌博游戏
二项分布是n个独立重复的是/非试验中成功次数的离散概率分布,这些概率是固定不变的,与试验结果无关。
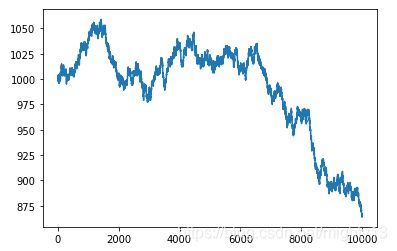
设想你来到了一个17世纪的赌场,正在对一个硬币赌博游戏下8份赌注。每一轮抛9枚硬币,如果少于5枚硬币正面朝上,你将损失8份赌注中的1份;否则,你将赢得1份赌注。我们来模拟一下赌博的过程,初始资本为1000份赌注。为此,我们需要使用random模块中的binomial函数。
为了理解binomial函数的用法,请完成如下步骤。
-
(1) 初始化一个全
0的数组来存放剩余资本。以参数10000调用binomial函数,意味着我们将在赌场中玩10000轮硬币赌博游戏。import numpy as np cash = np.zeros(10000) cash[0] = 1000 outcome = np.random.binomial(9, 0.5, size=len(cash)) -
(2) 模拟每一轮抛硬币的结果并更新
cash数组。打印出outcome的最小值和最大值,以检查输出中是否有任何异常值:for i in range(1, len(cash)): if outcome[i] < 5: cash[i] = cash[i - 1] - 1 elif outcome[i] < 10: cash[i] = cash[i - 1] + 1 else: raise AssertionError("Unexpected outcome " + outcome) print( outcome.min(), outcome.max() )不出所料,所有的结果值都在0~9之间:
0 9 -
(3) 使用Matplotlib绘制
cash数组:import matplotlib.pyplot as plt plt.plot(np.arange(len(cash)), cash) plt.show()
案例完整代码如下:
import numpy as np
import matplotlib.pyplot as plt
cash = np.zeros(10000)
cash[0] = 1000
outcome = np.random.binomial(9, 0.5, size=len(cash))
for i in range(1, len(cash)):
if outcome[i] < 5:
cash[i] = cash[i - 1] - 1
elif outcome[i] < 10:
cash[i] = cash[i - 1] + 1
else:
raise AssertionError("Unexpected outcome " + outcome)
print( outcome.min(), outcome.max() )
plt.plot(np.arange(len(cash)), cash)
plt.show()
6.19 超几何分布
超几何分布(hypergeometric distribution)是一种离散概率分布,它描述的是一个罐子里有两种物件,无放回地从中抽取指定数量的物件后,抽出指定种类物件的数量。NumPy random模块中的hypergeometric函数可以模拟这种分布。
6.20 动手实践:模拟游戏秀节目
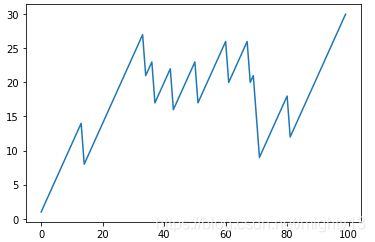
设想有这样一个游戏秀节目,每当参赛者回答对一个问题,他们可以从一个罐子里摸出3个球并放回。罐子里有一个“倒霉球”,一旦这个球被摸出,参赛者会被扣去6分。而如果他们摸出的3个球全部来自其余的25个普通球,那么可以得到1分。因此,如果一共有100道问题被正确回答,得分情况会是怎样的呢?为了解决这个问题,请完成如下步骤。
-
(1) 使用
hypergeometric函数初始化游戏的结果矩阵。该函数的第一个参数为罐中普通球的数量,第二个参数为“倒霉球”的数量,第三个参数为每次采样(摸球)的数量。import numpy as np points = np.zeros(100) outcomes = np.random.hypergeometric(25, 1, 3, size=len(points)) -
(2) 根据上一步产生的游戏结果计算相应的得分。
for i in range(len(points)): if outcomes[i] == 3: points[i] = points[i - 1] + 1 elif outcomes[i] == 2: points[i] = points[i - 1] - 6 else: print(outcomes[i]) -
(3) 使用Matplotlib绘制
points数组。import matplotlib.pyplot as plt plt.plot(np.arange(len(points)), points) plt.show()
案例完整代码如下:
import numpy as np
import matplotlib.pyplot as plt
points = np.zeros(100)
outcomes = np.random.hypergeometric(25, 1, 3, size=len(points))
for i in range(len(points)):
if outcomes[i] == 3:
points[i] = points[i - 1] + 1
elif outcomes[i] == 2:
points[i] = points[i - 1] - 6
else:
print outcomes[i]
plt.plot(np.arange(len(points)), points)
plt.show()
6.21 连续分布
连续分布可以用PDF(Probability Density Function,概率密度函数)来描述。随机变量落在某一区间内的概率等于概率密度函数在该区间的曲线下方的面积。NumPy的random模块中有一系列连续分布的函数——beta、chisquare、exponential、f、gamma、gumbel、laplace、lognormal、logistic、multivariate_normal、noncentral_chisquare、noncentral_f、normal等。
6.22 动手实践:绘制正态分布
随机数可以从正态分布中产生,它们的直方图能够直观地刻画正态分布。按照如下步骤绘制正态分布。
-
(1) 使用
NumPyrandom模块中的normal函数产生指定数量的随机数。import numpy as np N=10000 normal_values = np.random.normal(size=N) -
(2) 绘制分布直方图和理论上的概率密度函数(均值为0、方差为1的正态分布)曲线。
dummy, bins, dummy = plt.hist(normal_values, int(np.sqrt(N)), density=True, lw=1) sigma = 1 mu = 0 import matplotlib.pyplot as plt plt.plot(bins, 1/(sigma * np.sqrt(2 * np.pi)) * np.exp( - (bins - mu)**2 / (2 * sigma**2) ),lw=2) plt.show()
案例完整代码如下:
import numpy as np
import matplotlib.pyplot as plt
N=10000
normal_values = np.random.normal(size=N)
dummy, bins, dummy = plt.hist(normal_values, int(np.sqrt(N)),density=True, lw=1)
sigma = 1
mu = 0
plt.plot(bins, 1/(sigma * np.sqrt(2 * np.pi)) * np.exp( - (bins - mu)**2 / (2 * sigma**2) ),lw=2)
plt.show()
6.23 对数正态分布
对数正态分布(lognormal distribution) 是自然对数服从正态分布的任意随机变量的概率分布。NumPy random模块中的lognormal函数模拟了这个分布。
6.24 动手实践:绘制对数正态分布
我们绘制出对数正态分布的概率密度函数以及对应的分布直方图,步骤如下。
-
(1) 使用
NumPyrandom模块中的normal函数产生随机数。import numpy as np N=10000 lognormal_values = np.random.lognormal(size=N) -
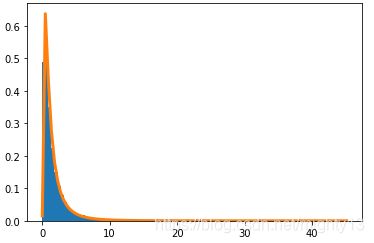
(2) 绘制分布直方图和理论上的概率密度函数(均值为0、方差为1)。
dummy, bins, dummy = plt.hist(lognormal_values,int(np.sqrt(N)),density=True, lw=1) sigma = 1 mu = 0 x = np.linspace(min(bins), max(bins), len(bins)) pdf = np.exp(-(np.log(x) - mu)**2 / (2 * sigma**2))/ (x * sigma * np.sqrt(2 * np.pi)) import matplotlib.pyplot as plt plt.plot(x, pdf,lw=3) plt.show()
直方图和理论概率密度函数的曲线相吻合。
案例完整代码如下:
import numpy as np
import matplotlib.pyplot as plt
N=10000
lognormal_values = np.random.lognormal(size=N)
dummy, bins, dummy = plt.hist(lognormal_values, int(np.sqrt(N)), density=True, lw=1)
sigma = 1
mu = 0
x = np.linspace(min(bins), max(bins), len(bins))
pdf = np.exp(-(np.log(x) - mu)**2 / (2 * sigma**2))/ (x * sigma * np.sqrt(2 * np.pi))
plt.plot(x, pdf,lw=3)
plt.show()