【1月学习进度1/31——论文阅读01】“Attention is All You Need”——Transformer模型
论文:Attention is All You Need
视频详解Transformer模型
(以下截图大部分来自于该视频)
论文逐段精度视频
0. 引言
1)为了解决什么任务
Transformer是为了解决机器翻译(machine translation tasks)任务提出的一种序列转录模型(sequence transduction model),序列转录即由序列1生成序列2。

2)序列建模与序列转录问题的研究状况
在Transformer提出之前的主流模型大都基于复杂循环或“编码-解码”结构的卷积神经网络,最好的模型采用注意力机制连接编码器和解码器。
① 循环神经网络RNN
RNN 善于处理序列数据(即后面数据与前面数据有关系),记忆以前的信息。
类比到 人通过已经掌握的知识能力来对当前问题作出抉择。
(例:LSTM → LSTM详解、GRU → GRU详解)
RNN的缺点:
通过前一个隐藏状态 h t − 1 h_{t-1} ht−1 和 当前态 x t x_t xt 得到下一个隐藏状态 h t h_t ht
明显的顺序性导致其有如下缺点:
- 时间上无法并行
- 若序列过长,随着隐藏层的传递,前期信息可能丢失,为了保证信息不丢失,需要扩大 h t h_t ht ,则会导致内存开销大
② 卷积神经网络CNN
为了减少顺序计算(RNN缺点),提高计算效率,采用卷积神经网络CNN来代替循环神经网络RNN,可并行计算。
CNN缺点:
“This makes it more difficult to learn dependencies between distant positions.”(论文原句)
对于长序列,学习相距较远位置的依赖性很难 → 难以对长序列进行建模
③ Attention注意力机制
克服CNN缺点,其对位置之间的依赖性的计算不考虑位置远近,即其可以看到整个输入的序列。
1. Transfomer的全局架构
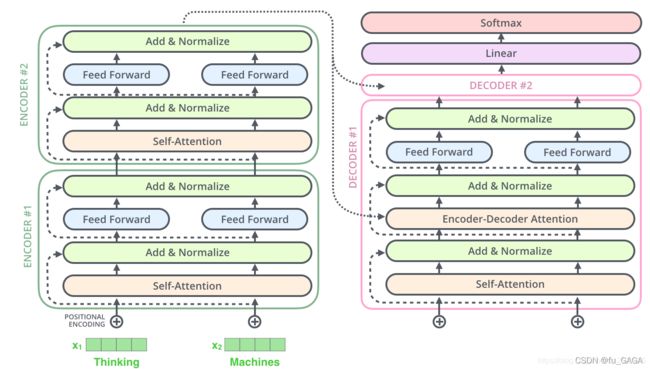
原论文中模型架构图:
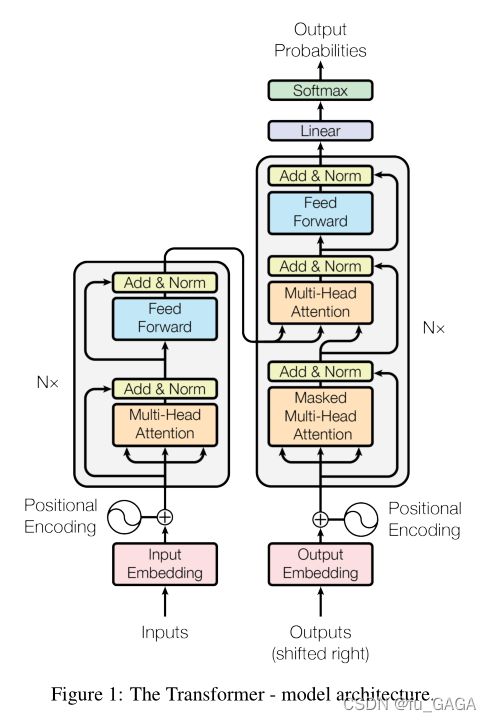
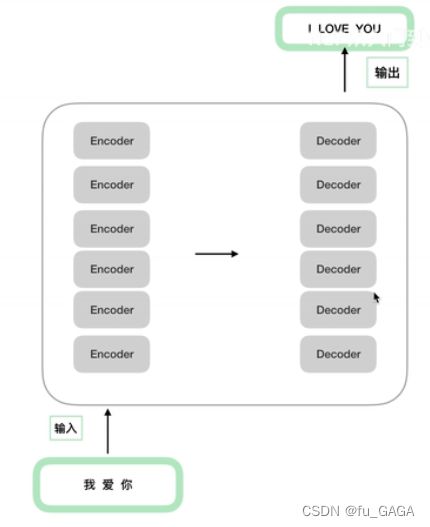
其中 N N Nx 表示多个Encoder和多个Decoder,多个Encoder结构相同,但每个单独训练,参数不同(Decoder同理)。
2. Transformer中Encoder编码器详解
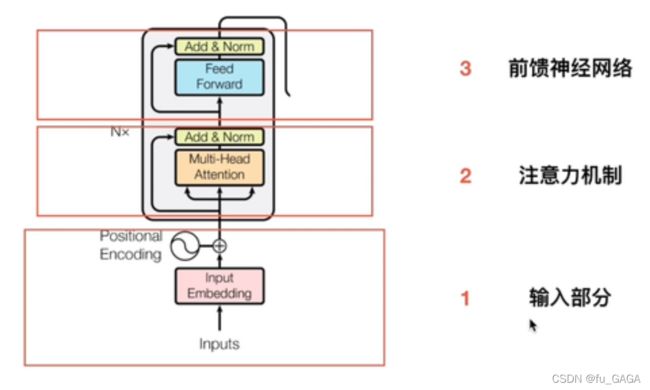
(1) 输入部分
1.Embedding

Embedding简言之,就是对于每一个词学习一个维度为d的向量表示,称为“词向量”。
2.位置编码Positional Encoding
❤ 为什么要进行位置编码?
RNN 提取序列信息时,将上一时刻的输出作为下一时刻的输入,从而保留了时序信息;
而Attention机制不考虑顺序,只是将序列中感兴趣的信息抽取出来
(若打乱词序,语义发生变化,但Attention结果不变,会出现错误)
因此,引入位置编码来表示时序信息(位置信息)
❤ 如何进行位置编码?
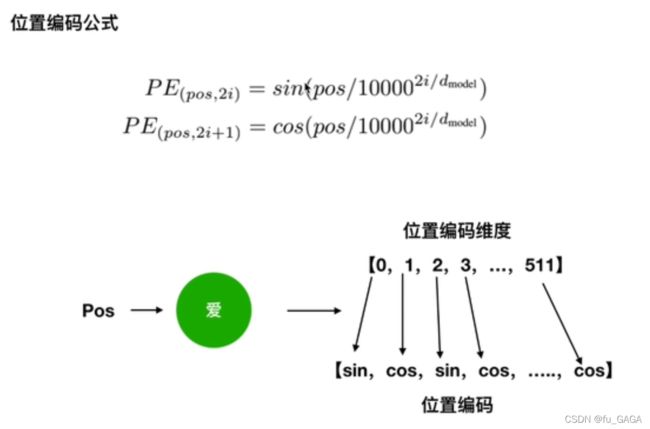
对于每个词Embedding后的词向量,偶数位置 2 i ( 0 , 2 , 4 , 6 , 8...510 ) 2i(0,2,4,6,8...510) 2i(0,2,4,6,8...510) 使用 s i n sin sin ,奇数位置 2 i + 1 ( 1 , 3 , 5 , 7...511 ) 2i+1(1,3,5,7...511) 2i+1(1,3,5,7...511) 使用 c o s cos cos。
❤ 位置嵌入?
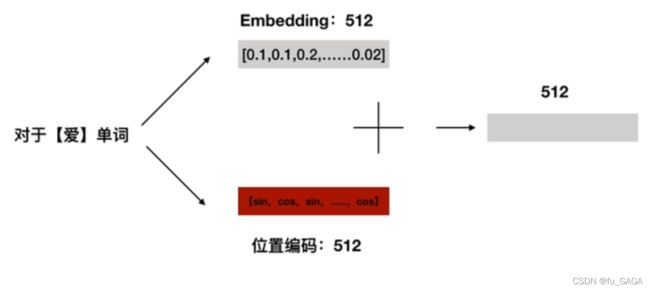
将每个单词Embedding后的512维词向量与其对应位置编码后的512维向量,对应维度相加,得到的512维向量作为输入。
(2)注意力机制
① 基本的注意力机制
key:键
value:键对应的值
query:查询(单词)
输入:query
权重计算:query和key的相似度(相似度越大,权重越大)
输出:value的加权和
基于不同的相似度衡量,有两种常用的注意力函数:
- additive attention
- dot-product attention(更有效)
(点乘 → 一个向量在另一个向量方向上的投影,标量,可以用来衡量向量的相似度,两个向量越相似,其点乘结果越大)
Example:
F ( Q , K ) F(Q,K) F(Q,K) 计算Query和Key的相似度
经过softmax归一化为和为1,其全为正数的值作为权重,计算value的加权和,得到Attention的输出。
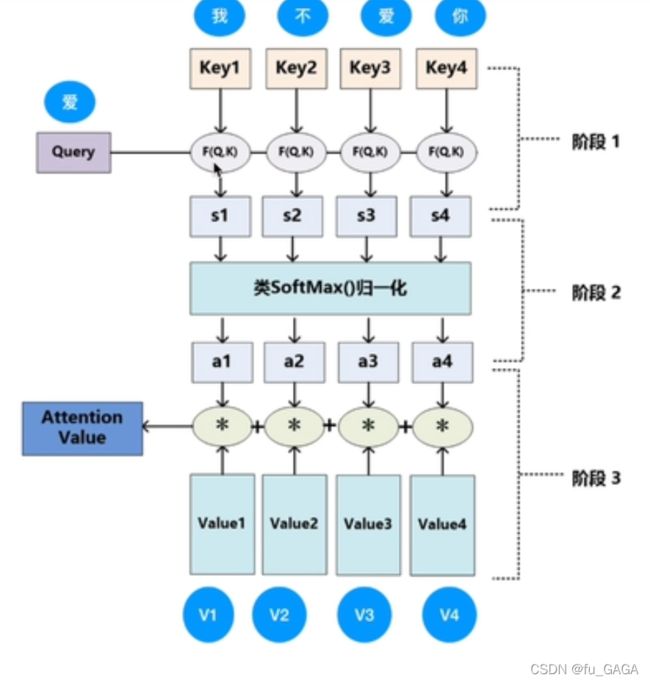
② Transformer中的注意力机制
图片来源 & 参考讲解: Transformer详解
❤ TRM中的Attention函数:
采用 点积
Scaled Dot-Product Attention
公式如下:
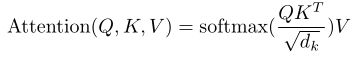
当 d k d_k dk 较大时,计算得到的点积结果也很大,导致做 s o f t m a x softmax softmax 后,大值会更接近于1,梯度较小,会引发梯度消失问题 → 点乘后乘 1 d k \frac{1}{\sqrt{d_k}} dk1
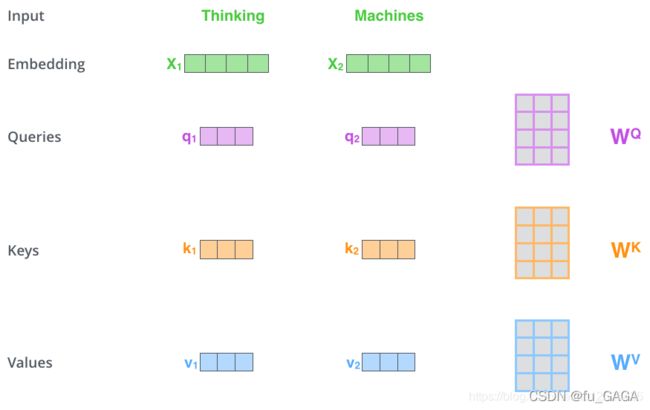
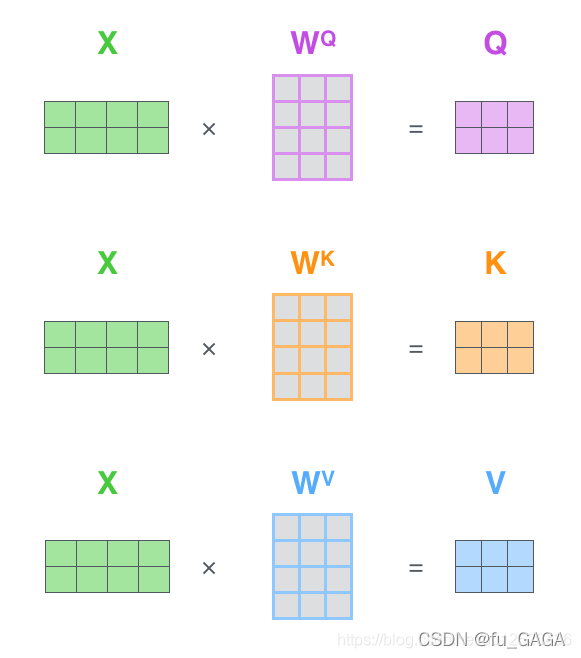
❤ TRM中如何获取 Q , K , V Q,K,V Q,K,V ?
其中 q , k , v q,k,v q,k,v 向量分别是用 随机初始化的矩阵 W Q , W K , W V W^Q,W^K,W^V WQ,WK,WV 与Embedding后的向量 X X X 相乘得到的,得到的向量维度由512维降低到64维
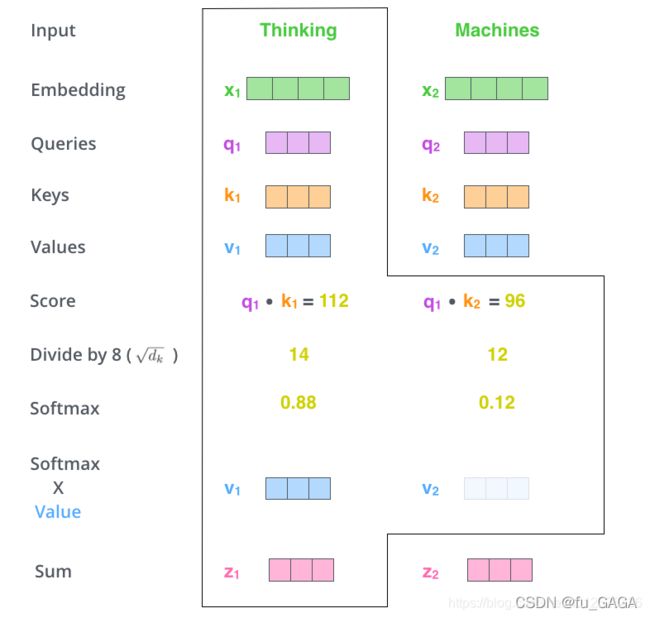
根据上述公式计算:
如 z 1 = 0.88 ∗ v 1 + 0.12 ∗ v 2 z_1=0.88*v_1+0.12*v_2 z1=0.88∗v1+0.12∗v2
实际上使用矩阵并行计算:
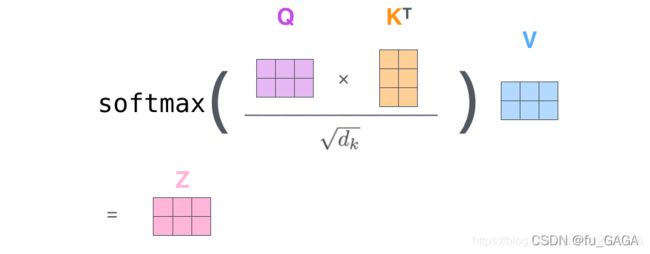
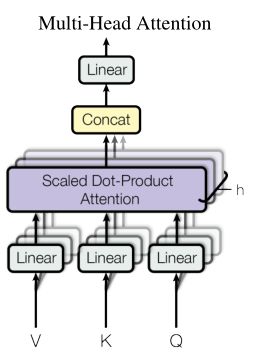
❤ Multi-Headed Attention 多头注意力机制
上述中相当于只使用了一套参数 W Q , W K , W V W^Q,W^K,W^V WQ,WK,WV,而原论文中采用8套参数,相当于投到多个不同的空间,分别提取信息
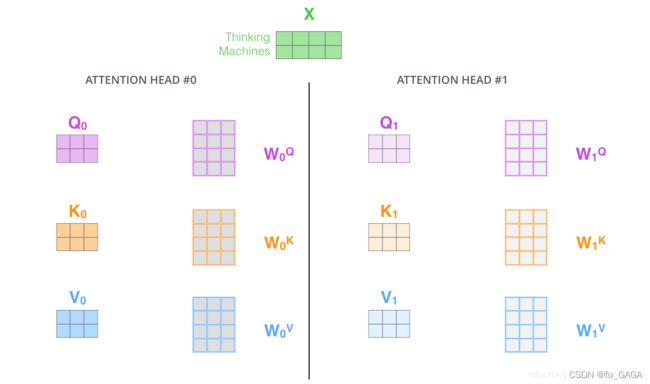
每一个头得到一个 Z i Z_i Zi
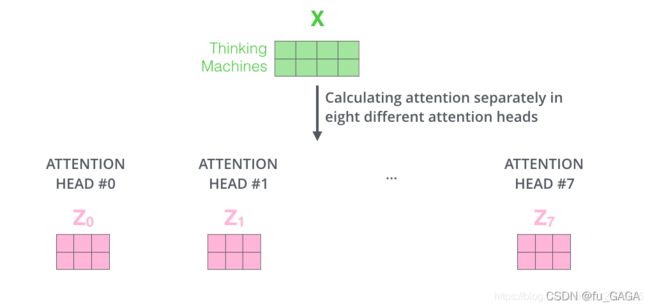
将所有头的输出合并为一个大矩阵,再与随机初始化的矩阵 W O W_O WO 相乘,得到最终多头注意力机制的输出 Z Z Z
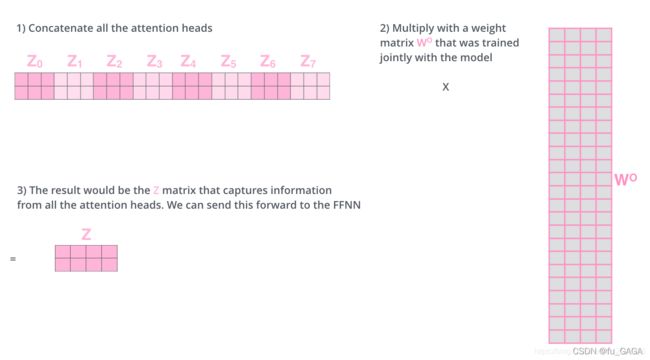
注意力机制提取与query相似度高的那些重要的value值,相当于提取相关的重要信息;
多头注意力机制是多个注意力机制的集成,但每个注意力机制单独学习不同的参数,最后的结果合并后再做一次线性投影。

(3)残差与LayerNorm
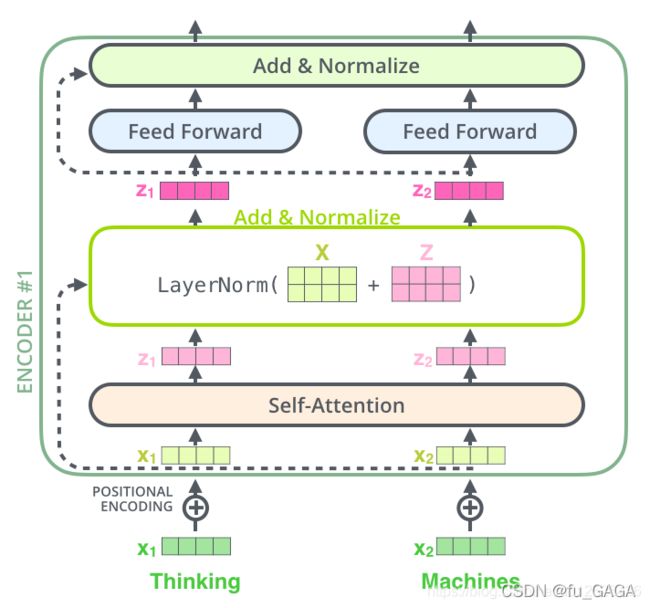
(图片来源: Transformer详解)
① 残差
本文中的残差连接:
其中子层有两种 : M u l t i − H e a d e d Multi-Headed Multi−Headed A t t e n t i o n Attention Attention 层和 F e e d Feed Feed F o r w a r d Forward Forward层
❤ 什么是残差?
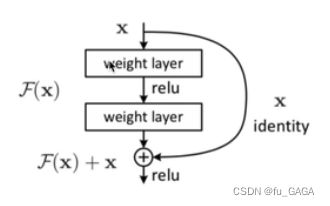
将上述图片抽象为如下的模块图
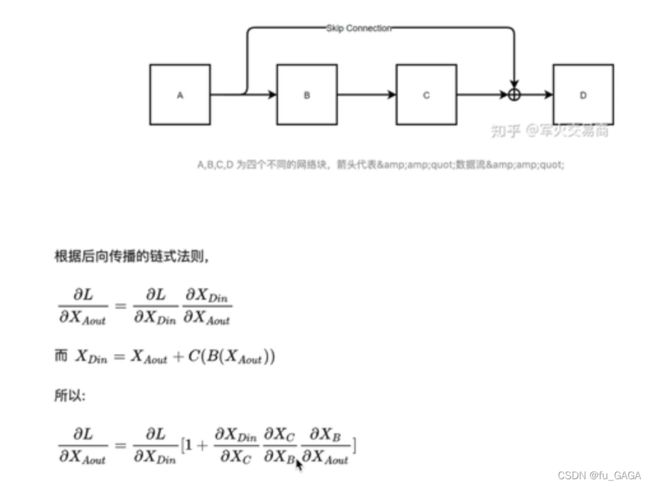
大部分梯度消失都是因为 连乘,最后梯度随着网络深度增加而变为0
❤ 残差作用:由上述式子可以知道,残差不会使梯度为0,所以可以增加网络深度,缓解梯度消失问题
② LayerNorm
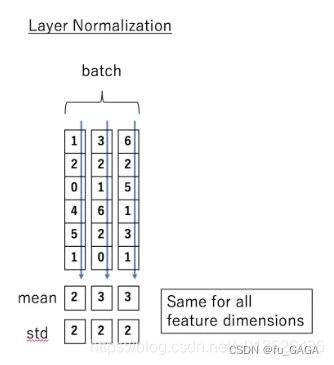
❤ 归一化:
- 目的:将数据归一到均值为0,方差为1(减均值 除方差)
- 常用方法:BatchNorm和LayerNorm
❤ 与BatchNorm区别:
- BatchNorm是对所有样本每个特征进行归一化(减均值,除方差)
下图中 x i x^i xi 为样本
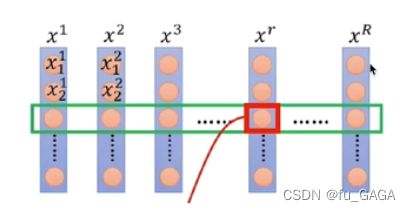
预测时需要将所有训练样本的均值与方差作为Normalization的均值与方差
缺点:
- 当batch_size较小时,效果较差(所有样本作为整体的估计)
- 序列长度不一致,尤其长度变化较大的样本,使得全局均值、方差抖动较大,并且若训练样本中序列长度都较小,预测时对于长序列预测将出现错误
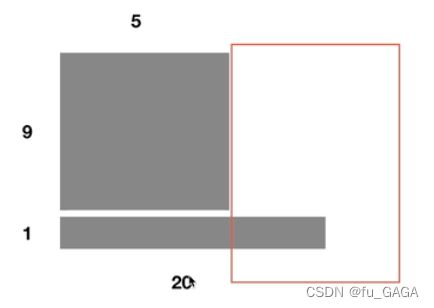
LayerNorm:对每个样本的所有特征做归一化
不需要将样本整体的均值方差作为预测时的均值方差,因为是针对每个样本求的均值方差。
❤ 为什么LayerNorm更适合NLP问题?
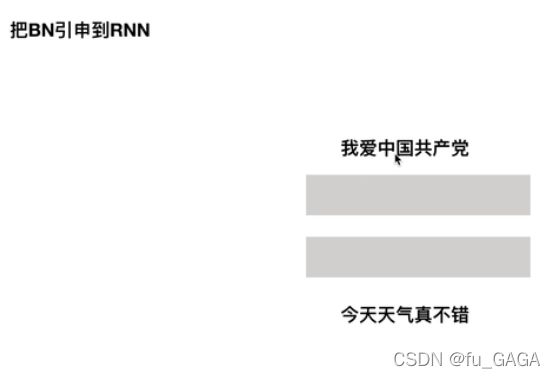
如上图中所示,若采用BN方法进行归一化,则BN将“我”-“今”、“爱”-“天”…做归一化,两个样本并不在同一个语义空间中。
LN将“我爱中国共产党”、“今天天气真不错”两个样本分别进行归一化。
3.Decoder详解
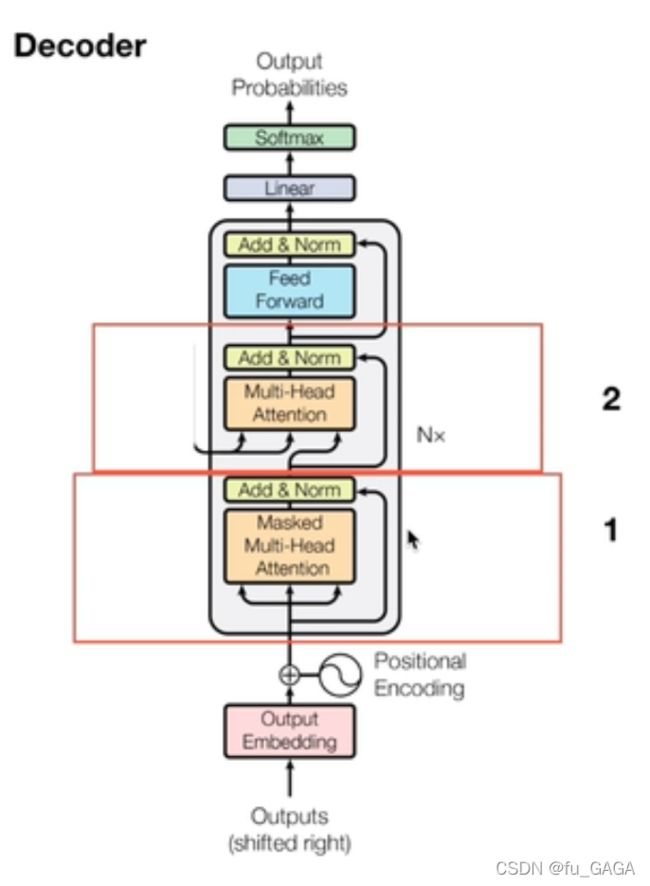
与Encoder的不同之处:
- 多头注意力机制增加了Mask
- 第二层中的多头注意力机制中的key和value的值来自于Encoder输出
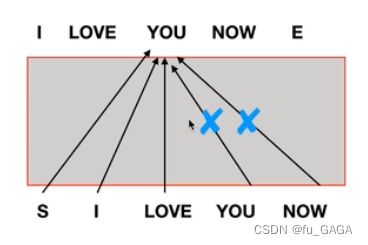
(1)为什么要mask?
mask —— 将某些参数值掩盖,使其在参数更新时不产生效果
mask目的 —— 不让decoder看到未来的序列信息
因此需要将该位置之后的序列屏蔽掉
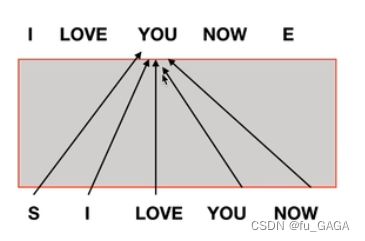
(2)与编码器的交互
Encoder的输出连接到所有Decoder的输入
如何连接:
- Encoder编码器的输出生成Decoder注意力机制中的 key、value,即 K , V K,V K,V 矩阵
- Decoder注意力机制中的query,即 Q Q Q 矩阵由上一个Decoder的输出生成
多个编码器-解码器相连结构如下: