《Attention is all you need》论文笔记

Abstract

一般来说，重要的 sequence transduction 模型都是基于包含 Encoder，Decoder 的复杂的 RNN 和 CNN 的。最好的模型是通过一个 attention 机制来连接 Encoder，Decoder。本文提出一种简单的架构——Transformer，只用注意力机制，和 CNN、RNN 没有关系。

在两个翻译任务实验证明该模型又快又好

1. WMT 2014 Englishto-German 翻译任务 BLEU 为 28.4，比当下 SOTA 高 2
2. 用 8 个 GPU 训练 3.5 天，在 WMT 2014 English-to-French 翻译任务 BLEU 41.8，为该任务 SOTA

1. Introduction

RNN，LSTM，GRU 在翻译和 LM（language model）领域效果很好，达到了很多 SOTA，很多研究花了很多心思在推进 Encoder-Decoder 和 Recurrent Language Model 的边界。

可是，RNN 的设计架构决定了训练的时候并行性差。尤其对长的 sequence，同时内存限制影响 batch examples。有一些通过分解 tricks 和条件计算来提高 efficiency 的 related work，后者也提高 performance。但是问题依然存在。

注意力机制可以不管句子长度的情况下得到依赖信息，但是注意力机制经常和 RNN 结合使用（限制了注意力机制的效果）。

这篇论文提出 Transformer，只用注意力机制而不用 RNN，能够捕获全局依赖，并行化，效果好，时间短。

2. Background

一些相关的研究都用了 CNN 来减少 sequence 计算。

这些模型里的计算随着输入输出距离的线性（convS2S）或是指数级（ByteNet）地增长，使得很难学习到较远距离的依赖。在 Transformer 里，这是一个常数级的操作，虽然是以牺牲一定精度为代价，但是论文用 Multi-Head Attention 来抵消了，效果很好。

Self-attention，通过结合一个 sequence 的不同位置来计算整个 sequence 的表征。成功用在阅读理解等任务。

Transformer 是最早的只依赖 self-attention 来计算其输入和输出的表示，而不使用序列对齐的 RNN 或 CNN。

3. Model Architecture

大部分神经序列转换模型（neural sequence transduction models）都有 encoder-decoder structure。此处，encoder 将输入的序列（x1, x2, … , xn）转换为连续的表示 z = (z1, z2, …, zn)。给定 **z，**decoder 然后每一输出一个元素，构成了序列 (y1, y2, … , ym)。在每一个时间步骤，该模型是 auto-regressive，当产生下一个输出时，会使用上一个时刻产生的符号作为额外的输入（consuming the previously generated symbols as additional input when generating the next）。

3.1 Encoder and Decoder Stacks

Encoder： encoder 是由 6 个相同的 layer 堆叠起来的。每一个 layer 包括 两个 sub-layers：

第一个是：mutli-head self-attention mechanism ;

第二个是：position-wise fully connected feed-forward network.

每一个这样的 two sub-layers 附近都会用上 residual connection（残差连接），然后加上 layer normalization

Decoder： decoder 也有 6 层。主要两个区别：

1. 增加了一个子层，将 encoder 的输出当做输入。
2. 修改了 decoder 栈的自注意力自层，来防止位置们去关注后续的位置。masking 结合 output 的 embedding 都右移了一位这个事实，保证了位置 i 的预测只依赖于比 i 小的已知位置。

3.2 Attention

An attention function can be described as mapping a query and a set of key-value pairs to an output, where the query, keys, values, and output are all vectors. 输出可以看做是 the values 的加权组合，给每一个 value 的加权可以计算为：a compatibility function of the query with the corresponding key.

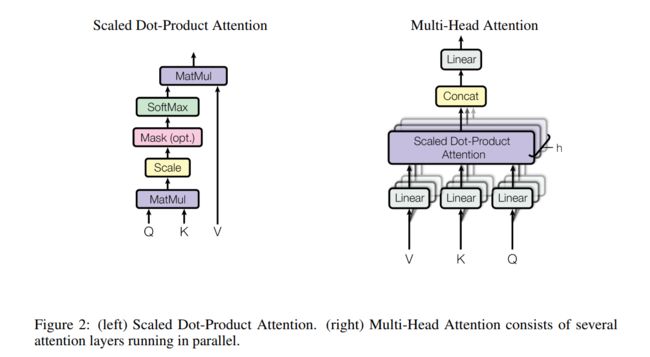
3.2.1 Scaled Dot-Product Attention

看过 Luong 那篇 attention 的文章的人都知道，score 一般有三种算法：
$$score(h_t,{\overline{h}}_s)=\{\begin{array}{ll}{h}_t^{\top }{\overline{h}}_s& dot\\ & \\ h_t^{\top }{W}_a{\overline{h}}_s& general\\ & \\ v_a^{\top }tanh(W_a[h_t;{\overline{h}}_s])& concat\end{array}$$
其实文章里用的就是第一种，因为性价比高（效果还不错速度快），但是有个缺点当 Q，K 的维度比较大的时候，容易进到 softmax 的饱和区，作者就 scale 了一下（除以 $\sqrt{d_k}$），解决了这个问题，这个就是所谓的 Scaled Dot-Product Attention。粗暴有效。
$$Attention(Q,K,V)=softmax(\frac{Q{K}^{\top }}{\sqrt{d_k}})V$$

3.2.2 Multi-Head Attention

文章表示，比起直接用 $d_{model}$ 的 Q, K, V 来说，将 Q, K, V 用不同的 h 个线性投影得到的 h 个 $d_v$ 的 context vector，再 concat 起来，过一个线性层的结果更好，可以综合不同位置的不同表征子空间的信息。
$$\begin{gathered} \text{Multihead}(Q,K,V)=\text{Concat}({\text{head}}_1,{\text{head}}_2,...,{\text{head}}_h)W^O \\ {\text{where head}}_i=\text{Attention}(Q{W}_i^Q,K{W}_i^K,V{W}_i^V) \end{gathered}$$
其中，$W_i^Q\in {\mathbb{R}}^{d_{model}\times d_k}$，$W_i^K\in {\mathbb{R}}^{d_{model}\times d_k}$，$$W_i^V\in {\mathbb{R}}^{d_{model}\times d_k}$$，$W^O\in {\mathbb{R}}^{h{d}_v\times d_{model}}$

在文章里，设置了 h=8 个平行注意层（也就是头（head））。对于每个层的 $d_k=d_v=d_{\text{model}}/h=64$。因为每个头都减少了 dimension，所以整体的 computational cost 和 single-head full dimension 的注意力机制是差不多的。

3.2.3 Applications of Attention in our model

• encoder 自身的 self-attention，Q K V 均来自于上一层输出，当前层的每个 position 可以 attend 到上一层的所有位置。
• deocder 自身的 self-attention，与 1 类似，除了采用 0-1mask 消除右侧单词对当前单词 attention 的影响。
• encoder-decoder attention，Query 来自 decoder 内部的上一层，K 和 V 均来自于 encoder 的输出。这一步操作模拟了传统机器翻译中的 attention 过程（信息的交互）。

3.3 Position-wise Feed-Forward Networks

每个 FFN 包括两次线性变换，中间是 ReLu 的激活函数。
$$\text{FFN}=\max (0,x{W}_1+b_1)W_2+b_2$$
不同 position 的 FFN 是一样的，但是不同层是不同的。输入输出维度都是 $d_{model}=512$，中间层的维度是 $d_{ff}=2048$。

3.4 Embeddings and Softmax

和其他序列转换模型一样，我们利用学习到的 embeddings 来转换输入的符号，然后输出符号为维度是 $d_{model}$ 的向量。embedding 层，会把权重乘 $\sqrt{d_{model}}$

3.5 Positional Encoding

因为模型没有 RNN 或者 CNN，为了用到 sequence 的顺序，作者引入了 positional encoding（$dim=d_{model}$，便于相加）来加入一些相对位置的信息。
$$\begin{gathered} PE(pos,2i)=sin(pos/10000^{2i/d_{model}}) \\ PE(pos,2i+1)=cos(pos/10000^{2i/d_{model}}) \end{gathered}$$
作者测试用学习的方法来得到 PE，最终发现效果差不多，所以最后用的是 fixed 的，而且 sinusoidal 的可以处理更长的 sequence 的情况。

用 sinusoidal 函数的另一个好处是可以用前面位置的值线性表示后面的位置。
$$\begin{gathered} \sin (\alpha +\beta )=\sin \alpha \cos \beta +\cos \alpha \sin \beta \\ \cos (\alpha +\beta )=\cos \alpha \cos \beta -\sin \alpha \sin \beta \end{gathered}$$

4. Why Self-Attention

之所以选择 self-attention，主要因为三点：

• 每层的 computational complexity；
• 可以被 parallelize 的计算量；
• 网络中 long-range dependencies 直接的 path length（越短越能方便学到 long-range dependencies）。

5. Conclusion

优点：

1. 抛弃了 RNN 和 CNN，提出了 Transformer，算法的并行性非常好；
2. Transformer 的设计最大的带来性能提升的关键是将任意两个单词的距离是 1，有效地解决了 long dependency 的问题。

缺点：

1. Transformer 不像 CNN 那样可以抽取局部特征，RNN + CNN + Transformer 的结合可能会带来更好的效果；
2. 位置信息其实在 NLP 中非常重要，Transformer 中用的 Position Embedding 也不是一个最终的解决方案。

参考链接

【论文笔记】Attention is all you need

论文笔记：Attention Is All You Need