软件设计师——程序设计语言练习
一、单选题
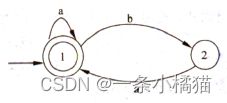
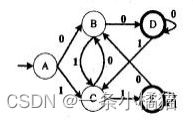
1.以下关于下图所示有限自动机的叙述中,不正确的是( )
A、该自动机识别的字符串中a不能连续出现
B、该自动机识别的字符串中b不能连续出现
C、该自动机识别的非空字符串必须以a结尾
D、该自动机识别的字符串可以为空串
正确答案:A
【解析】1既是初态也是终态,从图中可以看出a能连续出现,保持在状态1。
2.下图所示有限自动机的特点是( )
A、识别的0、1串是以0开头且以1结尾
B、识别的0、1串中1的数目为偶数
C、识别的0、1串中0后面必须是1
D、识别的0、1串中1不能连续出现
正确答案:D
【解析】对于题中自动机的状态图,先忽略状态q0的自环(识别若干个0),从初态q0到终态q1,该自动机可识别的字符串为1、101、10101、…,显然,该自动机识别的0、1串中1不能连续出现。
从初始态q0输入0仍然到q0或者输入1到达终态q1,从q1还可以输入0重新到达初始态q0,所以这个有限自动机识别的0、1串不一定是以0开头的,1的数目的奇偶性也没办法确定,0后面也可以是0,所以选项A、B、C都是错误的。从q0输入1到达终态q1后,或者串结束,或者输入0再到q0,所以这个串中的1不会连续出现,选项D是正确的。
3.下图所示的有限自动机中,0是初始状态,3是终止状态,该自动机可以识别( )
A、abab
B、aaaa
C、bbbb
D、abba
正确答案:B
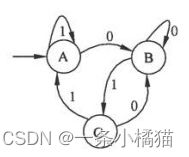
4.下图所示为两个有限自动机M1和M2 (A是初态、C是终态),( )
A、M1和M2都是确定的有限自动机
B、M1和M2都是不确定的有限自动机
C、M1是确定的有限自动机,M2是不确定的有限自动机
D、M1是不确定的有限自动机,M2是确定的有限自动机
正确答案:D
【解析】在本题中给出的图M1中,我们可以看到当在状态A输入0时,它可以转移到它自己,也可以转移到状态B,所以M1是非确定的。而M2中不存在这样的情况,因此是确定的有限自动机。
(1)不确定的有限自动机(NFA):对每一个可能的输入可以有多个状态转移,从接受到输入,从多个状态转移中不确定的地选择一个。
(2)确定的有限自动机(DFA):对每一个可能地输入只有一个状态的转移。
二者最大的区别是它们的转移函数不同。
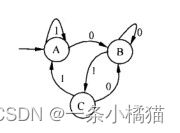
5.下图所示为一个有限自动机(其中,A是初态、C是终态),该自动机识别的语言可用正规式 表示
A、(0|1)*01
B、1*0*10*1
C、1*(0)*01
D、1*(0|10)*1*
正确答案:A
【解析】
(1)被有限自动机所识别是指从初态开始到终态结束,所输入的字符串能够按顺序地执行下去,若到某个状态不能往下走得到下一个字符,则认为不能识别。
(2)在本题中,选项A能被识别。从初态A出发,不管经过多少个1和0之后,只能是处在A、B、C三种状态中的一种,所以在(0|1)*后,只能是处在A、B、C三种状态中的一种,不管是在那个状态,输入0后,都会处在状态B,然后输入1,都会转换到状态C,因此选项A能被该有限自动机所识别。同样的道理,我们可以知道其它选项的正规式不能被识别。(*代表无限多次的意思)。
(3)题中的自动机,从A出发到达C结束的所有路径必然包含BC这条弧(标记为1),同时到达B的弧上都标记了0,所以其识别的字符串必须以01结尾。
补充正则式:
正规式:由正规文法转换而来,通常正规文法等价于正规式。
| 文法产生式 | 正规式 | |
|---|---|---|
| 规则1 | A→xB, B→y | A=xy |
| 规则2 | A→xA|y | A=x*y |
| 规则3 | A→x, A→y | A=x|y |
*表示可以出现0次或任意多次
x|y表示可能x、也可能是y
| 正规式 | 正规集 |
|---|---|
ab |
符号串ab构成的集合 |
|
|
字符串a、b构成的集合 |
a* |
由0个或多个a构成的符号串集合 |
|
|
所有字符a和b构成的串的集合 |
|
|
a为首字符的a、b字符串集合 |
|
|
以abb结尾的a、b字符串的集合 |
ab:只有一种情况,就是 ab
a|b:有两种情况,a或者b
a*:有无数种情况
6.下图所示为一个有限自动机(其中,A是初态、C是终态),该自动机所识别的字符串的特点是( )。
A、必须以11结尾的0、1串
B、必须以00结尾的0、1串
C、必须以01结尾的0、1串
D、必须以10结尾的0、1串
正确答案:C
此题和上题一样,问法不一样。
【解析】
(1)被有限自动机所识别是指从初态开始到终态结束,所输入的字符串能够按顺序地执行下去,若到某个状态不能往下走得到下一个字符,则认为不能识别。
(2)在本题中,选项A能被识别。从初态A出发,不管经过多少个1和0之后,只能是处在A、B、C三种状态中的一种,所以在(0|1)*后,只能是处在A、B、C三种状态中的一种,不管是在那个状态,输入0后,都会处在状态B,然后输入1,都会转换到状态C,因此选项A能被该有限自动机所识别。同样的道理,我们可以知道其它选项的正规式不能被识别。(*代表无限多次的意思)。
(3)题中的自动机,从A出发到达C结束的所有路径必然包含BC这条弧(标记为1),同时到达B的弧上都标记了0,所以其识别的字符串必须以01结尾。
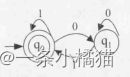
7.某非确定的有限自动机(NFA)的状态转换图如下图所示(q0既是初态也是终态)。以下关于该NFA的叙述中,正确的是( )
A、其可识别的0、1序列的长度为偶数
B、其可识别的0、1序列中0与1的个数相同
C、其可识别的非空0、1序列中开头和结尾字符都是0
D、其可识别的非空0、1序列中结尾字符是1
正确答案:D
【解析】
8.某确定的有限自动机 (DFA) 的状态转换图如下图所示 (A 是初态,D、E 是终态),则该 DFA 能识别( )
A、00110
B、10101
C、11100
D、11001
正确答案:C
【解析】选项中,只有C选项的字符串能被DFA解析。解析路径为:ACEEBDD。
9.某确定的有限自动机(DFA)的状态转换图如下图所示(0是初态,4是终态),则该DFA能识别( )
A、aaab
B、abab
C、bbba
D、abba
正确答案:A
【解析】B项从0到1然后走不了了,C项在3状态结束,不对;D项也只到1状态。
10.算术表达式a+(b-c)*d的后缀式是()
A、b c - d * a +
B、a b c - d * +
C、a b + c - d *
D、a b c d - * +
正确答案:B
【解析】后缀式就是后序遍历,左→右→根,根据算术表达式画出这棵二叉树。
后缀式是abc-d*+
11.与逆波兰式ab-cd+*对应的中缀表达式是( )
A、a-b+c*d
B、(a-b)*c+d
C、(a-b)*(c+d)
D、a-b*c+d
正确答案:C
【解析】
逆波兰式是后缀式,就是后序遍历,左→右→根,根据逆波兰式画出这棵二叉树,中缀表达式就是中序遍历,左→根→右。
中缀表达式是a-b*c+d
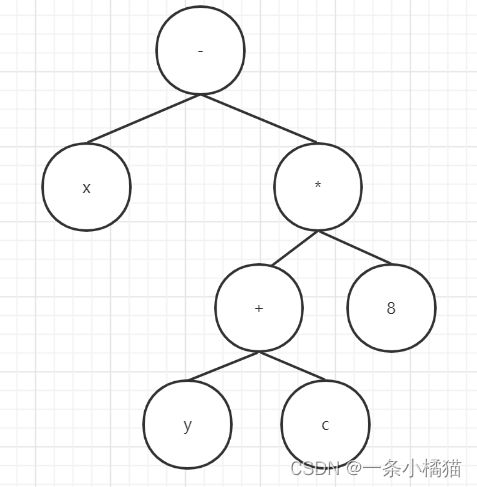
12.算术表达式x-(y+c)*8的后缀式是()
A、xyc8-+*
B、xy-c+8*
C、xyc8*+-
D、xyc+8*-
正确答案:D
【解析】后缀式就是后序遍历,左→右→根,根据算术表达式画出这棵二叉树。
后缀式是xyc+8*-
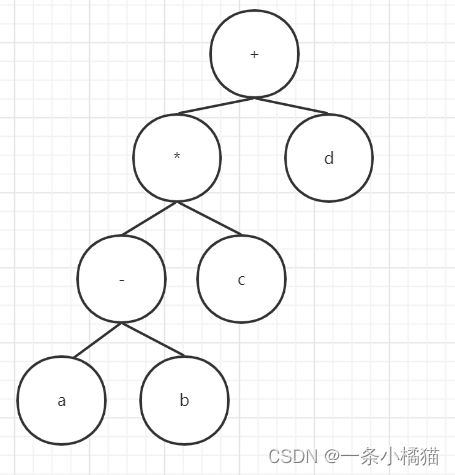
13.算术表达式(a-b)*c+d的逆波兰式是( )
A、abcd -*+
B、ab —cd* +
C、ab-c*d+
D、abc-d*+
正确答案:C
【解析】逆波兰式是后缀式,就是后序遍历,左→右→根,根据算术表达式画出这棵二叉树。
逆波兰式是ab-c*d+
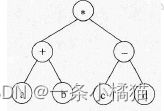
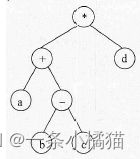
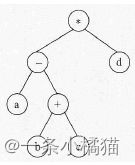
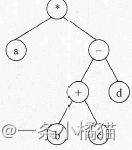
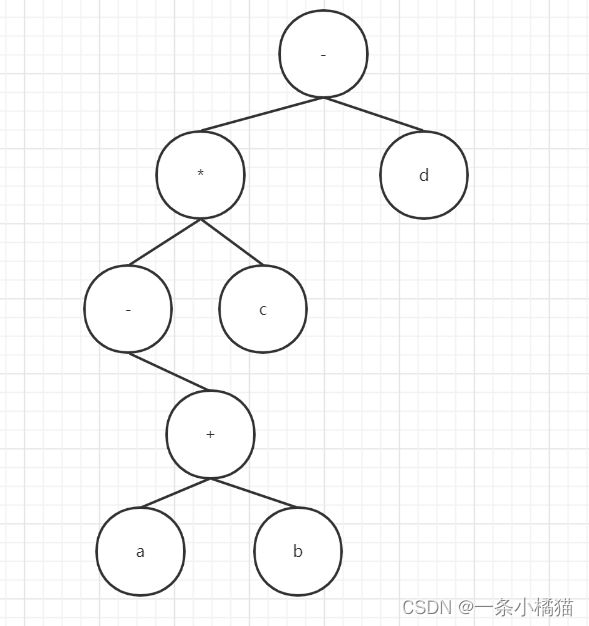
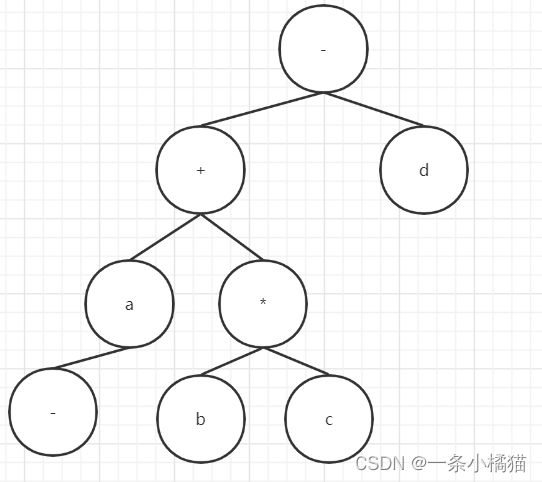
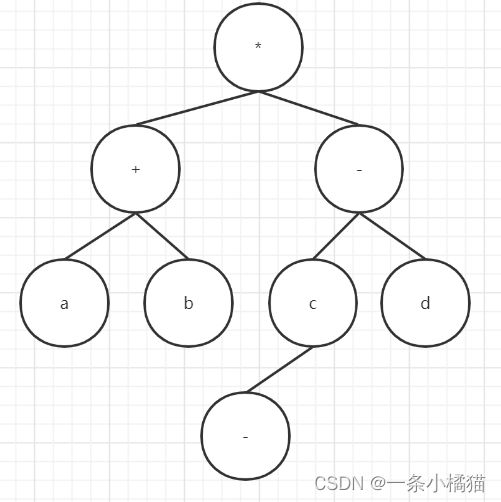
14.与算术表达式“(a+(b-c))*d“ 对应的树是( )
正确答案:B
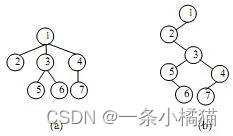
15.若将某有序树 T 转换为二叉树 T1,则 T 中结点的后(根)序序列就是 T1 中结点的()遍历序列。例如,下图(a)所示的有序树转化为二叉树后如图(b)所示。
A.先序 B.中序 C.后序 D.层序
所属知识点:数据结构与算法基础>数与二叉树的特性
答案解析:
本题考查数据结构中二叉树基本知识。
对树可进行先根遍历、后根遍历和层序遍历。例如,对题中(a)所示树进行先根遍历的序列为1、2、3、5、6、4、7,后根遍历的序列为2、5、6、3、7、4、1,层序遍历序列为1、2、3、4、5、6、7。
对二叉树可进行先序遍历、中序遍历、后序遍历和层序遍历。对题中(b)所示二叉树进行遍历,先序序列为1、2、3、5、6、4、7,中序序列为2、5、6、3、7、4、1,后序序列为6、5、7、4、3、2、1,层序序列为1、2、3、5、4、6、7。
显然,将树转换为二叉树后,树的先根序列等于对应二叉树的先序序列,树的后根序列等于对应二叉树的中序序列。
16.与逆波兰式ab+ -c*d-对应的中缀表达式是()。
A.a-b-c*d B.-(a+b)*c-d C.-a+b*c-d D.(a+b)*(-c-d)
所属知识点:程序设计语言>后缀表达式
答案解析:
本题考查表达式的表示方式。
表达式的逆波兰表示也就是后缀表示,在表达式的这种表示方法中,将运算符号写在运算对象的后面,并指明其前面的操作数或中间结果所要执行的运算。对后缀表达式从左到右求值,则每当扫描到一个运算符号时,其操作数是最近刚得到的。因此“ab+-c*d-”表示:先将a与b相加,然后作一元“-”运算,结果再与c相乘,乘运算的结果再与d相减,因此中缀表达式的形式为“-(a+b)*c-d”。
逆波兰式是后缀式,就是后序遍历,左→右→根;中缀表达式是中序遍历,也是算术表达式,左→根→右,根据中缀表达式画出ABCD四个选项的二叉树。