【Matlab数学建模】层次分析法
一、通过权重表格求解评价类问题
层次分析法主要用于评价类问题,比如说小明要去旅游,纠结去苏航还是北戴河、还是桂林。
我们可以弄这样一张权重表格。

将这张表格记作矩阵:
A = ( a 11 a 12 a 13 a 14 a 21 a 22 a 23 a 24 a 31 a 32 a 33 a 34 a 41 a 42 a 43 a 44 a 51 a 52 a 53 a 54 ) A = \begin{pmatrix} a_{11} & a_{12} & a_{13} & a_{14}\\ a_{21} & a_{22} & a_{23} & a_{24}\\ a_{31} & a_{32} & a_{33} & a_{34}\\ a_{41} & a_{42} & a_{43} & a_{44}\\ a_{51} & a_{52} & a_{53} & a_{54} \end{pmatrix} A=⎝⎜⎜⎜⎜⎛a11a21a31a41a51a12a22a32a42a52a13a23a33a43a53a14a24a34a44a54⎠⎟⎟⎟⎟⎞
取m为权重表矩阵的行数,n为权重表矩阵的列数,则对于权重矩阵而言,需满足:
∑ i = 1 m a i 1 = 1 对 于 ∀ i ∈ [ 1 , m ] , 有 ∑ j = 2 n a i j = 1 \sum\limits_{i = 1}^{m}a_{i1} = 1\\ 对于\forall i \in \left[1, m\right],有\sum\limits_{j = 2}^{n}a_{ij}=1 i=1∑mai1=1对于∀i∈[1,m],有j=2∑naij=1
而我们计算权重值也很简单,例如计算第j列对应的权重值。
w j = ( a 11 , a 21 … a m 1 ) × ( a 1 j , a 2 j … a m j ) T w_{j}=\left(a_{11}, a_{21}\dots a_{m1}\right) \times \left(a_{1j}, a_{2j}\dots a_{mj}\right)^T wj=(a11,a21…am1)×(a1j,a2j…amj)T
然后我们比较w2、w3……wn。获得其中的最大值,即是最终答案。
例如在上面那个例子中
A = ( a 11 a 12 a 13 a 14 a 21 a 22 a 23 a 24 a 31 a 32 a 33 a 34 a 41 a 42 a 43 a 44 a 51 a 52 a 53 a 54 ) w 苏 杭 = ( a 11 , a 21 , a 31 , a 41 , a 51 ) × ( a 12 , a 22 , a 32 , a 42 , a 52 ) T w 北 戴 河 = ( a 11 , a 21 , a 31 , a 41 , a 51 ) × ( a 13 , a 23 , a 33 , a 43 , a 53 ) T w 桂 林 = ( a 11 , a 21 , a 31 , a 41 , a 51 ) × ( a 14 , a 24 , a 34 , a 44 , a 54 ) T A = \begin{pmatrix} a_{11} & a_{12} & a_{13} & a_{14}\\ a_{21} & a_{22} & a_{23} & a_{24}\\ a_{31} & a_{32} & a_{33} & a_{34}\\ a_{41} & a_{42} & a_{43} & a_{44}\\ a_{51} & a_{52} & a_{53} & a_{54} \end{pmatrix}\\ w_{苏杭} = (a_{11}, a_{21}, a_{31}, a_{41}, a_{51}) \times (a_{12}, a_{22}, a_{32}, a_{42}, a_{52})^T\\ w_{北戴河} = (a_{11}, a_{21}, a_{31}, a_{41}, a_{51}) \times (a_{13}, a_{23}, a_{33}, a_{43}, a_{53})^T\\ w_{桂林} = (a_{11}, a_{21}, a_{31}, a_{41}, a_{51}) \times (a_{14}, a_{24}, a_{34}, a_{44}, a_{54})^T A=⎝⎜⎜⎜⎜⎛a11a21a31a41a51a12a22a32a42a52a13a23a33a43a53a14a24a34a44a54⎠⎟⎟⎟⎟⎞w苏杭=(a11,a21,a31,a41,a51)×(a12,a22,a32,a42,a52)Tw北戴河=(a11,a21,a31,a41,a51)×(a13,a23,a33,a43,a53)Tw桂林=(a11,a21,a31,a41,a51)×(a14,a24,a34,a44,a54)T
计算完成后,比较三者大小选最大的。
用matlab程序可以表示为:
function res = func(mat)
[~, n] = size(mat);
a = sum(repmat(mat(:, 1), 1, n - 1) .* mat(:, 2 : n));
res = find(a == max(a));
end
二、如何获得权重表
首先,例子评价的指标有五个:景色、花费、居住、饮食、交通。构建一个五行五列方阵:
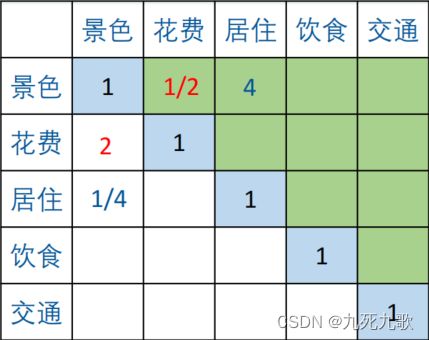
我们问问小明觉得景色和花费哪个重要,小明说觉得景色比花费重要两倍,所以 a 12 = 1 a 21 = 2 a_{12} = \frac{1}{a_{21}} = 2 a12=a211=2,小明还说居住比景色重要四倍。那么 a 31 = 1 a 13 = 4 a_{31} = \frac{1}{a_{13}} = 4 a31=a131=4
显然地,对于我们构建的这个矩阵,满足:
对 于 ∀ i , j ∈ [ 1 , n ] , 有 a i j × a j i = 1 对于\forall i, j\in[1, n],有a_{ij} \times a_{ji} = 1 对于∀i,j∈[1,n],有aij×aji=1
所有满足这个条件的矩阵都被成为正互反矩阵。可以用下面的的程序来判断:
function res = func(mat)
a = mat .* mat';
a = a(:);
res = all(a == 1);
end
对于某个正互反矩阵,若满足秩为一,即:
{ a i j > 0 a 11 = a 22 = ⋯ = a n n = 1 [ a i 1 , a i 2 , … , a i n ] = k i [ a 11 , a 12 , … , a 1 n ] \left\{ \begin{aligned} a_{ij}>0 \\ a_{11} = a_{22} = \dots = a_{nn} = 1\\ [a_{i1}, a_{i2}, \dots, a_{in}] = k_i[a_{11}, a_{12}, \dots, a_{1n}] \end{aligned} \right. ⎩⎪⎨⎪⎧aij>0a11=a22=⋯=ann=1[ai1,ai2,…,ain]=ki[a11,a12,…,a1n]
则称该矩阵为一致性矩阵。
而检验一个正互反矩阵是否接近于一致性矩阵的过程叫做一致性检验。其过程如下:

function [res, CR] = func(mat)
RI = [0.00 0.00 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59];
[n, ~] = size(mat);
lambda = max(eig(mat));
CI = (lambda - n) / (n - 1);
CR = CI / RI(n);
res = CR < 0.1;
end
三、求权重的三种方法
① 算术平均法求权重
function res = func(mat)
[n, ~] = size(mat);
res = sum((mat ./ repmat(sum(mat), n, 1)), 2) / n;
end
② 几何平均法
function res = func(mat)
[n, ~] = size(mat);
res = prod(mat, 2) .^ (1 / n);
res = res / sum(res);
end
③ 特征值法(最常用)
function res = func(mat)
[v, d] = eig(mat);
d = diag(d);
a = v(:, d == max(d));
res = a / sum(a);
end




