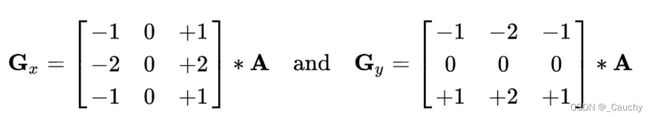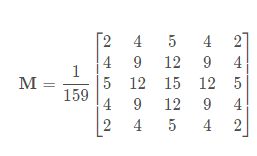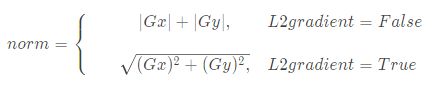Opencv 入门（三）

图像梯度

Sobel算子

• dst= cv2.Sobel(src, ddepth, dx, dy, ksize)

  • ddepth：图像深度,都是默认-1，表示输入输出深度一样
  • dx,dy：分别表示水平和竖直方向， 置1表示计算该方向
  • ksize：是Sobel算子的大小，表示核的大小

第二个参数，使用 -1 表示输出与输入图像的数据类型一致。如果原图是uint8型，那么在sobel算子计算后，得到的图像可能会有负值，负值会被截断为0或者255。
两种方式：

1. 改变输出图像的数据类型（第二个参数：cv2.CV_64F）
2. 改变原始图像的数据类型，那么第二个参数可以是 -1

如果ksize=-1，默认3x3 的Scharr 滤波器，效果优于 3x3 的Sobel 滤波器

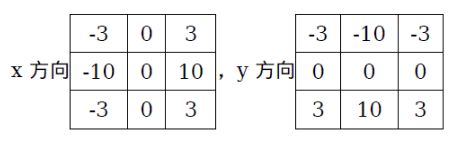
x, y方向的卷积核：

右边 - 左边，差异值作为水平方向
下面 - 上面，差异值作为垂直方向

由于只采用了2个方向的模板，只能检测水平和垂直方向的边缘，因此这种算法对于纹理较为复杂的图像，其边缘检测效果就不是很理想。该算法认为：凡灰度新值大于或等于阈值的像素点时都是边缘点。这会造成边缘点的误判，因为许多噪声点的灰度值也很大。

sobelx = cv.Sobel(img, cv.CV_64F, 1, 0, ksize=3)
sobelx = cv.convertScaleAbs(sobelx) # 绝对值转换, 负值取绝对值
sobely = cv.Sobel(img, cv.CV_64F, 0, 1, ksize=3)
sobely = cv.convertScaleAbs(sobely)
# 建议的做法，是利用 addWeighted 加权 x，y方向的图像，dx=1 && dy=1 效果较差
sobelxy = cv.addWeighted(sobelx, 0.5, sobely, 0.5, 0)
res = np.hstack((sobelx, sobely, sobelxy))
show("res", res)

灰图读入，同上用法展示：

---

Scharr 算子

• dst = cv2.Scharr(src,ddepth,dx,dy,scale,delta,borderType)

  • src： 原图像
  • ddepth： 输出图像的深度，该值与函数cv2.Sobel()中的参数ddepth的含义相同
  • dx： x方向上的求导阶数
  • dy： y方向上的求导阶数
  • scale： 计算导数时采用的缩放因子，默认为1，是没有缩放的
  • delta： 加在目标图像dst上的值，默认为0
  • borderType： 边界样式，默认值为cv2.BORDER_DEFAULT

scharr算子与Sobel的不同点是在平滑部分，这里所用的平滑算子是1/16∗[3,10,3]，相比于1/4∗[1,2,1]，中心元素占的权重更重，这可能是相对于图像这种随机性较强的信号，邻域相关性不大，所以邻域平滑应该使用相对较小的标准差的高斯函数，也就是更瘦高的模板。对一些细线，更敏感，更能描绘出。

• Sobel算子与Scharr算子比较：
  Sobel算子的缺点是，当结构较小时，精确度不高，Scharr算子具有更高的精度。

---

Laplacian算子

• dst = cv2.Laplacian(src,ddepth,ksize,scale,delta,borderType)

  • src： 原图像
  • ddepth： 输出图像的深度。
  • ksize： 计算二阶导数的核尺寸大小，必须为正的奇数。
  • scale： 计算导数时采用的缩放因子，默认为1，是没有缩放的
  • delta： 加在目标图像dst上的值，默认为0
  • borderType： 边界样式，默认值为cv2.BORDER_DEFAULT

Laplacian算子是一种二阶导数算子，具有旋转不变性，可以满足不同方向的边缘检测要求。通常其算子的系数之和需要为0。

---

Canny边缘检测

• 使用高斯滤波器，以平滑图像，滤除噪声
• 计算图像中每个像素点的梯度强度和方向
• 应用非极大值抑制（Non-Maximun Suppression, NMS），以消除边缘检测带来的杂散响应
• 应用双阈值（Double-Threshold）检测来确定真实的和潜在的边缘
• 通过抑制孤立的弱边缘最终完成边缘检测

1. 高斯滤波

   大小为*(2k + 1) x (2k + 1)*的高斯滤波器核的生成方程式由下式给出：

一般选用 5 × 5 的核，（注意需要归一化）

2. 计算梯度强度和方向

• 梯度的方向与边缘的方向总是垂直的，通常取八个不同的方向计算梯度。
• 再用边缘检测算子（Sobel）计算图像的水平，垂直，对角梯度，得到水平Gx和垂直Gy方向的一阶导数值，由此便可以确定像素点的梯度G的大小θ。
  $$G=\sqrt{(G_x^2+G_y^2)}$$
  $$\theta =arctan(\frac{G_x}{G_y})$$

角度一般是近似到8个方向上

3. 非极大值抑制(NMS)

非极大值抑制是一种边缘稀疏技术，非极大值抑制的作用在于“瘦”边。非极大值抑制可以将局部最大值之外的所有梯度值抑制为0。
对梯度图像中每个像素进行非极大值抑制的算法是：

1. 将当前像素的梯度强度与沿正负梯度方向上的两个像素进行比较。
2. 如果当前像素的梯度强度与另外两个像素相比最大，则该像素点保留为边缘点，否则该像素点将被抑制。

经过上述处理后，对于同一个方向的若干边缘点，基本上只保留了一个，因此实现了边缘细化的目的。
如下图，A , B , C 三点中，梯度方向上A点的局部梯度值最大，所以保留A点，其余两点被抑制。

4. 用双阈值算法检测和连接边缘

经过上述步骤后，图像内的强边缘已经在当前获取的边缘内，但是，一些虚边缘也在内。

设置两个阈值，高阈值maxVal、低阈值minVal。
根据边缘梯度值和阈值关系，判断边缘的属性：

• 梯度值 ≥ maxVal， 强边缘

• minVal < 梯度值 < maxVal， 虚边缘

  • 虚边缘与强边缘相连时，则保留。

• 梯度值 ≤ minVal， 抑制当前边缘

实际中maxVal：minVal = 2：1的比例效果比较好

5. 抑制孤立低阈值点

到目前为止，被划分为强边缘的像素点已经被确定为边缘，因为它们是从图像中的真实边缘中提取出来的。然而，对于弱边缘像素，将会有一些争论，因为这些像素可以从真实边缘提取也可以是因噪声或颜色变化引起的。为了获得准确的结果，应该抑制由后者引起的弱边缘。通常，由真实边缘引起的弱边缘像素将连接到强边缘像素，而噪声响应未连接。为了跟踪边缘连接，通过查看弱边缘像素及其8个邻域像素，只要其中一个为强边缘像素，则该弱边缘点就可以保留为真实的边缘。

抑制孤立边缘点的伪代码描述如下：

• Canny

  • cv2.Canny(image,threshold1,threshold2,apertureSize,L2gradient)

    • image ：输入图像，必须为8位图像
    • threshold1： 第一个阈值
    • threshold2：第二个阈值
    • apertureSize： Sobel算子的大小
    • L2gradient： 计算图像梯度幅度的表示。默认值为False，使用L1范数计算；如果为True，则使用更精确的L2范数计算。
      

# 灰图读入
img = cv.imread(name + '_3.2.jpg', cv.IMREAD_GRAYSCALE)
# 高斯去噪
img = cv.GaussianBlur(img, (3, 3), 0)
# Canny检测
canny1 = cv.Canny(img, 128, 200)
canny2 = cv.Canny(img, 32, 128)

show('origin', img)
show('canny1', canny1)
show('canny2', canny2)

图像金字塔

图像金字塔是图像中多尺度表达的一种，最主要用于图像的分割，是一种以多分辨率来解释图像的有效但概念简单的结构。图像金字塔最初用于机器视觉和图像压缩，一幅图像的金字塔是一系列以金字塔形状排列的分辨率逐步降低，且来源于同一张原始图的图像集合。其通过梯次向下采样获得，直到达到某个终止条件才停止采样。金字塔的底部是待处理图像的高分辨率表示，而顶部是低分辨率的近似。我们将一层一层的图像比喻成金字塔，层级越高，则图像越小，分辨率越低。

---

高斯金字塔

高斯金字塔用来向下降采样图像，注意降采样其实是由金字塔底部向上采样，分辨率降低，它和我们理解的金字塔概念相反（注意）

• 对图像的向下取样操作，即缩小图像
  

• 对图像的向上取样，即放大图像
  

down_up = cv.pyrUp(cv.pyrDown(img))
show('res', np.hstack((img, down_up)))

---

拉普拉斯金字塔

$$L_i=G_i-PyrUp(PyrDown(G_i))$$

拉普拉斯金字塔是通过源图像减去先缩小后再放大的图像的一系列图像构成的。保留的是残差！为图像还原做准备！

down_up = cv.pyrUp(cv.pyrDown(img))
show('res', img - down_up)

注意：上采样和下采样是非线性处理，不可逆，有损的处理！

---

轮廓检测

• 调用流程和方法

  • 载入图像
  • 灰度化
  • 二值化
  • 轮廓检测

---

• contours, hierarchy = cv2.findContours(image, mode, method)

返回的参数

• contours：检测到的轮廓，每个轮廓是由一些点构成的向量组成
• hierarchy：记录轮廓之间的关系，四个维度分别代表：同级后一个轮廓的序号、同级上一个轮廓的序号、第一个孩子序号，父亲序号

第二个数参数mode是检测轮廓的层级关系排列规则：

• RETR_EXTERNAL：仅仅检测外圈轮廓
• RETR_LIST：检测所有轮廓，但没有层级关系
• RETR_CCOMP：仅仅两层包含关系，即只有外层和内层。假设有夹层，那么夹层也算外层，只要某个轮廓还包含有轮廓，都算外部轮廓
• RETR_TREE：检测所有的轮廓，并建立完整的层级关系（常用）

第三个参数method是轮廓点的存储方式：

• CHAIN_APPROX_NONE：相邻的轮廓点坐标只相差一个像素，所以是连续轮廓点
• CHAIN_APPROX_SIMPLE：横、竖、对角线段只保存断点数据，比如矩形就只保存四个顶点。

画图函数

• image = cv2.drawContours(image, contours, contourIdx, color[, thickness[, lineType …]] )

输入参数：

• contours：是list类型的数组，里面存储了很多array数组去代表各个轮廓
• contourIdx：从上面的轮廓list中取出哪一个画出来，-1代表全部
• color：线条颜色
• thickness：线条粗细，-1代表填充式画轮廓，整个轮廓内部被指定颜色填充
• lineType：线条类型，虚线、实线之类的

注意：如果将原图传入画图函数，这个原图会被画上轮廓。

img = cv.imread(name + '_1.jpg')
gray = cv.cvtColor(img, cv.COLOR_BGR2GRAY)
ret, thresh = cv.threshold(gray, 127, 255, cv.THRESH_BINARY)
contours, hierarchy = cv.findContours(thresh, cv.RETR_TREE, cv.CHAIN_APPROX_NONE)

img1 = img.copy()
res = cv.drawContours(img1, contours, -1, (0, 0, 255), 1)
show('res', res)

轮廓特征

面积

• cv2.contourArea()

求出指定轮廓的面积

cv.contourArea(contours[1])

周长

• cv2.arcLength()

求出指定轮廓的周长，第二个参数指示当前输入为闭合轮廓(True)还是非闭合曲线(False)

cv.arcLength(contours[1], True)

轮廓近似

多边形

cnt = contours[100]
epsilon = 0.1 * cv.arcLength(cnt, True)
# 新的轮廓的周长和原始轮廓周长的误差范围在原周长的十分之一以内

approx = cv.approxPolyDP(cnt, epsilon, True)
img1 = img.copy()
res = cv.drawContours(img1, [approx], -1, (0, 0, 255), 2)
show('res', res)

边界矩形

x,y,w,h = cv.boundingRect(cnt)
img = cv.rectangle(img, (x, y), (x+w, y+h), (0, 255, 0), 2)
show('img', img)

外接圆

(x, y), radius = cv.minEnclosingCircle(cnt)
center = (int(x), int(y))
radius = int(radius)
show('img', cv.circle(img.copy(), center, radius, (0, 255, 0), 2))