小白学冈萨雷斯数字图像处理——第九章：形态学图像处理
注：笔者水平有限，此博客目的为学习记录，方便以后复习。
9.1 预备知识
本节介绍一些集合理论中的基本概念，并讨论MATLAB的逻辑运算符对于二值图像的应用。
9.1.1 集合论中的基本概念
若(x,y)是Z^2中的整数，f是为每对不同的坐标(x,y)分配亮度值（即来源于实数集R中的实数）的映射，则函数f(x,y)称为数字图像。
除去基本的交并运算外，形态学运算中通常还需要两个运算符，这两个运算符是特别针对于元素均为像素坐标的集合的，定义如下：
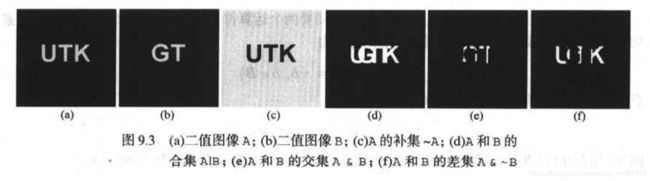
9.1.2 二值图像、集合和逻辑运算符
一副二值图像可以看成是x,y的二值函数，形态学理论中把二值图像看成是其前景像素的集合（1值）。二值图像间可以进行集合的交并运算，之后仍为二值图像；若A和B中的像素为前景像素，运算后仍为前景像素。
9.2 膨胀和腐蚀
9.2.1 膨胀
膨胀是在二值图像中“加长”或“变粗”的操作。这种特殊的方式和变粗的程度由一个称为结构元素的集合控制。
膨胀运算的过程如下：结构元素的原点必须标明，之后，将该结构元素的原点在原图像上平移，元素内有1与原图像中的1重合时，结构元素原点所在的点变为1值。
数学上，膨胀定义为集合运算：
可使用imdilate()函数执行膨胀运算
A2 = imdilate(A,B);
膨胀可应用于图像增强：
9.2.2 膨胀元素的分解
膨胀满足结合律，因此，结构元素可以进行分解。又因为计算膨胀所需要的时间正比于结构元素中非零元素的个数，因而可以通过对结构元素进行分解减少运算时间。
例如，一个55的全1结构元素，可以分解为15的全1结构元素与5*1的全1结构元素相膨胀，速度可提升约2.5倍。
9.2.3 函数strel
函数strel用于构造各种形状和大小的结构元素，其基本语法为：
se = strel(shape,parameters)
其中，shape是指定希望形状的字符串，parameters是指定形状信息（如大小）的一列参数。
strel不显示通常的MATLAB矩阵，而是返回一个称为strel对象的特殊量,显示其邻域、结构元素中值为1的像素数、分解中的结构元素数以及分解中的结构元素中值为1的总像素数。函数getsequence可用于提取并检查分解其中的单个结构元素。
decomp = getsequence(se);
strel型对象，在imdilate处理过程中会自动使用分解信息来加快膨胀过程。
9.2.4 腐蚀
腐蚀“收缩”或“细化”二值图像中的对象。收缩同样由一个结构元素控制。
其运算过程如下图所示：即只有完全匹配是才为1，否则置0。
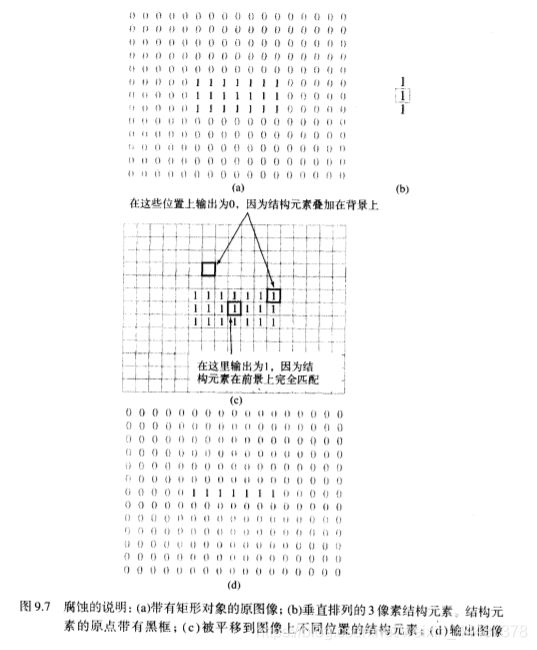
腐蚀的数学定义如下：
腐蚀用函数imerode来实现。当我们想要去除图像中的细线，但想保留其他结构时，可以通过选取一个足够小的结构元素来匹配中心方块实现。
9.3 膨胀与腐蚀的组合
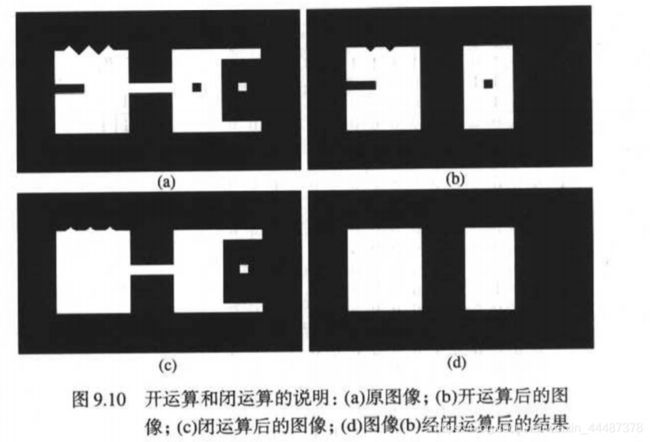
9.3.1 开运算和闭运算
A被B形态学开运算：A被B腐蚀后再用B来膨胀得到的腐蚀结果，即：
**应用：**形态学开运算完全删除了不能包含结构元素的对象区域，平滑了对象的轮廓，断开了狭窄的连接，去掉了细小的突出部分。
A被B的形态学闭运算与开运算相反，即先膨胀再腐蚀。
应用：形态学闭运算也会平滑对象的轮廓，但一般会将狭窄的缺口连接起来形成细长的弯口，并填充比结构元素小的洞。
形态学开运算与闭运算可用MATLAB工具箱函数imopen imclose实现。
C1 = imopen(A,B);
C2 = imclose(A,B);
A是一副二值图像，B可用strel生成。
应用：
9.3.2 击中或击不中变换
击中或击不中变换用于识别像素的特定形状，例如孤立的前景像素或线段的端点像素。定义如下：
击中或击不中变换由函数bwitmiss实现：
C = bwitmiss(A,B1,B2);
击中或击不中变换可用于定位：
9.3.3 使用查找表
当击中或击不中元素较小时，计算击中或击不中变换的较快方法是使用查找表（LUT）。这种方法是预先计算出每个可能邻域形状的像素值，然后把这些值存储到一个表中，以便以后使用。
工具箱中提供两个函数实现此功能。其中makelut基于一个提供给用户的函数构造一个查找表，函数applylut则使用这个查找表来处理二值图像。
例如，在上例中，使用makelut写一个能接收33矩阵并返回一个单值的矩阵，并对每个可能的33矩阵调用512次，它以512个数的向量的形式返回。
在此我们编写一个endpoints用于检测边缘点。
function g = endpoints(f);
persistent lut
if isempty(lut)
lut = makelut(@endpoint_fcn,3);
end
g = applylut(f,lut);
function is_end_point = endpoint_fcn(nhood)
is_end_point = nhood(2,2) & (sum(nhood(:)) == 2)
应用：
function out = conwaylaws(nhood)
num_neighbors = sum(nhood(:)) ~ nhood(2,2);
if nhood(2,2) == 1
if num_neighbors <= 1
out = 0;
else if num_neighbors >= 4
out = 0;
else
out = 1;
end
else
if num_neighbors == 3
out = 1;
else
out = 0;
end
end
lut = makelut(@conwaylaws,3); %使用上述函数调用makelut，可构建查找表
bw1 = [] %此处为初始图象
imshow(bw1,'n');
bw2 = applylut(bw1,lut);
imshow(bw2,'n');
bw3 = applylut(bw2,lut);
imshow(bw3,'n');
9.3.4 函数bwmorph
bwmorph函数可以执行膨胀、腐蚀、查找表等多种操作。
g = bwmorph(f,operation,n)
f为输入图像，operation指定操作，n指定重复操作次数，当n为Inf时表示重复操作直至不变。
9.4 标注连接分量
一个坐标为(x,y)的像素p有两个水平和两个垂直的相邻像素，其集合记为N4（p），称为四邻域；同理，若是8个方向则称为八邻域。若元素q属于N4§，则称p和q为四邻接；若元素q属于N8§，则称p和q八邻接。
若在前景像素p和q之间存在一条完全由前景像素组成的4连接路径，则称这两个前景像素为4连接。若存在8连接路径则称为8连接。对任意前景像素p,与其连接的所有前景像素的集合称为包含p的连接分量。
bwlabel函数可用于计算一副二值图像中的所有连接分量。
[L num] = bwlabel(f,conn) #conn默认为8
可通过该方法计算和显示连接分量的质心
f = imread('123.jpg');
[L,n] = bwlabel(f);
[r,c] = find(L == 3) #将返回属于第三个对象的所有像素的行索引和列索引
rbar = mean(r);
cbar = mean(c);
imshow(f)
hold on
for k = 1:n
[r,c] = find(L == k);
rbar = mean(r);
cbar = mean(c);
plot(cbar,rbar,'Marker','o','MarkerEdgeColor','k'...'MarkerFaceColor','k','MarkerSize',10);
plot(cbar,rbar,'Marker','*','MarkerEdgeColor','w');
end
9.5 形态学重构
重构是一种涉及到两幅图像和一个结构元素的形态学变换。一幅图像为标记，是变换的开始点，另一幅图像为掩膜，用来约束变换过程，结构元素用于定义连接性。如下讨论的B是一个大小为3*3且值为1的矩阵，其中心坐标为（2，2）。
可以用函数imreconstruct实现。
out = imreconstruct(marker,mask);
9.5.1 由重构做开运算
形态学开运算，先腐蚀去除小的对象，再膨胀恢复保留下来图像的形状，但其还原精度取决于形状和结构元素之间的相似性。本节用重构作开运算，精度更高。
9.5.2 填充孔洞
g = imfill(f,'holes');
9.5.3 清除边界对象
g = imclearborder(f,conn);
9.6 灰度图像形态学
除了击中或击不中变换外，其他的二值形态学操作都可以扩展到灰度图像上。、
9.6.1 膨胀和腐蚀
膨胀腐蚀可以组合使用。例如，从膨胀后的图像减去腐蚀后的图像可以产生一个“形态学梯度”，他是检测图像中局部灰度级变化的一种度量。
morph_grad = imsubtract(gd,ge);
9.6.2 开运算和闭运算
可以使用交替顺序滤波使图像更加平滑。（先开运算再闭运算或先闭运算再开运算）
fasf = f;
for k = 2:5
se = strel(disk,'k');
fasf = imclose(imopen(fasf,se),se);
end
顶帽变换：从原图像中减去开运算后的图像称为顶帽变换。
f = imtophat(f,se);
底帽变换：从原图像中减去闭运算后的结果称为底帽变换。
f = imbothat(f,se);
应用：（1）二者一起使用可以用于增强对比度。
se = strel('disk',3);
g = imsubtract(imadd(f,imtophat(f,se)),imbothat(f,se))
（2）颗粒分析
确定一副图像中颗粒大小分布。对于形状规则且亮于背景的颗粒，基本方法是应用不断增大尺寸的形态学开运算。对于每一个开运算，开运算中所有像素值的和会被计算；该和有时称为图像的表面积。下面是对半径为0到35的圆盘形开运算。
f = imread('123.jpg');
sumpixels = zeros(1,36);
for k = 0:35
se = strel('disk',k);
fo = imopen(f,se);
sumpixels(k+1) = sum(fo(:));
end
9.6.3 重构
应用：删除复杂图像的背景
#执行开运算重构——提取水平相邻键之间的背景
f = imread('calculator.jpg');
f_bor = imreconstruct(imerode(f,ones(1,71)),f);
f_o = imopen(f,ones(1,71));
#顶帽重构
f_thr = imsubtract(f,f_obr);
f_th = imsubtract(f,f_o);
#通过使用一条短水平线执行开运算重构来消除键右侧的垂直反射光
g_obr = imreconstruct(imerode(f_thr,ones(1,11)),f_thr);
#膨胀恢复被误消的字符
g_obrd = imdilate(g_obr,ones(1,21));
#将f_thr作为掩膜，将min(g_obrd,f_thr)作为标记，进行重构
f2 = imreconstruct(min(g_obrd,f_thr),f_thr);
