【剑指offer】——与二叉树遍历相关的习题练习1
文章目录
- 一、树的子结构
- 二、从上到下打印二叉树
-
- 2.1、广度优先遍历
- 2.2分行从上到下打印二叉树
- 2.3“之”字型打印二叉树
一、树的子结构
1、题目要求
输入两棵二叉树A和B,判断B是不是A的子结构,二叉树的结点定义如下:
struct BinaryTreeNode
{
double m_data;
BinaryTreeNode* leftchild;
BinaryTreeNode* rightchild;
};
2、题目分析
我们还是以具体的例子来加以讨论,如下的两棵树,分别为A树和B树。
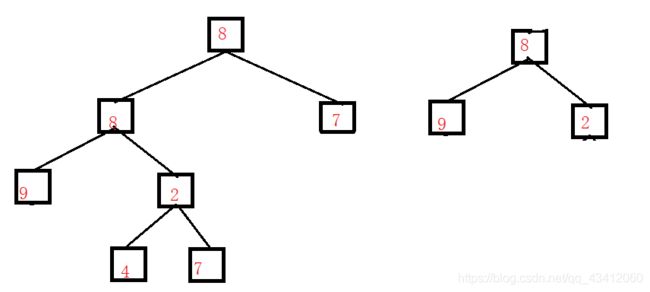
要查找树A中是否存在和树B结构一样的子树。我们可以分成两步来执行。第一步:在树A中找到和树B的根结点的值一样的结点R;第二步:判断树A中以R为根结点的子树是不是包含树B一样的结构。
我们可以采用递归的方式加以实现,首先,从数A的根结点开始遍历,我们发现他的根结点就是数字8,接着判断树A的根结点下面的子树是不是含有和树B一样的子结构,此时左子树8不等于9,所以我们仍然需要再次遍历树A,接着查找值为8的结点,如此往复操作以达到找到子结构的数为止。
有了上述的思路,我们就可以来着手于代码的实现了,因为我们采用递归的方式来实现,所以我们要使用两个函数,第一个函数HasSubtree主要用于递归调用遍历树A,如果发现某一结点的值和树B的头结点相同,则递归调用下一个函数DoseTree1HaveTree用于第二步相应子树结点的判断。其中一个细节值得我们多加注意,因为结点值的类型是double型,所以在判断值相等的时候不能单纯的使用==来判断,判断两个小数是否相等,只能判断他们之差的绝对值是不是在一个很小的范围内。具体实现如下:
bool Equal(double num1, double num2)
{
if ((num1 - num2 > -0.0000001) && (num1 - num2) < 0.0000001)
return true;
else
return false;
}
HasSubtree函数实现如下:
bool HasSubtree(BinaryTreeNode* pRoot1, BinaryTreeNode* pRoot2)
{
bool result = false;
if (pRoot1 != nullptr && pRoot2 != nullptr)
{
if (Equal(pRoot1->m_data, pRoot2->m_data))
result = DoseTree1HaveTree(pRoot1, pRoot2);
if (!result)
result = HasSubtree(pRoot1->leftchild, pRoot2);
if (!result)
result = HasSubtree(pRoot1->rightchild, pRoot2);
}
return result;
}
DoseTree1HaveTree实现如下:
bool DoseTree1HaveTree(BinaryTreeNode* pRoot1, BinaryTreeNode* pRoot2)
{
if (pRoot1 == nullptr)
return false;
if (pRoot2 == nullptr)
return true;
if (!Equal(pRoot1->m_data, pRoot2->m_data))
return false;
if (DoseTree1HaveTree(pRoot1->leftchild, pRoot2->leftchild) && DoseTree1HaveTree(pRoot1->rightchild, pRoot2->rightchild))
return true;
}
二、从上到下打印二叉树
2.1、广度优先遍历
1、题目要求
从上到下打印出二叉树的每一个结点,同一层的结点按照从左到右的顺序打印。其实就是一,种广度优先遍历的方式
2、题目分析
广度优先的遍历方式已经是我们再熟悉不过的一种二叉树遍历算法了,这里就不再赘述了,简洁的说就是利用一个队列,从根结点开始,每次打印一个结点的时候,如果该结点有子结点,则把该结点的子结点放到队列的末尾,接下来到队列的头部取出一个结点进行打印即可,不断重复上述操作。队列的结构实现也很简单,就使用STL中现成的deque即可。具体代码实现如下:
void PrintFromTopToBottom(BinaryTreeNode* pTreeRoot)
{
if (!pTreeRoot)
return;
std::deque<BinaryTreeNode*> dequeTreeNode;
dequeTreeNode.push_back(pTreeRoot);
while (dequeTreeNode.size())
{
BinaryTreeNode* pNode = dequeTreeNode.front();
dequeTreeNode.pop_front();
printf("%d",pNode->m_data);
if (pNode->leftchild)
dequeTreeNode.push_back(pNode->leftchild);
if (pNode->rightchild)
dequeTreeNode.push_back(pNode->rightchild);
}
}
2.2分行从上到下打印二叉树
1、题目要求:
从上到下按层打印二叉树,同一层的结点按从左到右的顺序打印,每一层打印到一行。
2、题目分析
深入理解题意,我们会发现这道题和上一题很相似,不同之处就是在打印的时候,要分层打印出来而不是全部都属于一层这样子打印。所以,我们要使用两个变量。一个变量表示当前层中还没有打印的节点数toBeprint,另外一个变量表示下一层结点的数目nextLevel。如果一个结点有子结点,就把每一个结点加入队列,同时把变量nextLevel加一,每打印一个结点,则变量toBeprint减一。当toBeprint为0的时候打印换行符,并把两个变量的值更新。
代码实现如下:
void Print(BinaryTreeNode* pRoot)
{
if (pRoot == nullptr)
return;
std::queue<BinaryTreeNode*> nodes;
nodes.push(pRoot);
int nextLevel = 0;
int toBeprint = 1;
while (!nodes.empty())
{
BinaryTreeNode* pNode = nodes.front();
printf("%d", pNode->m_data);
if (pNode->leftchild != nullptr)
{
nodes.push(pNode->leftchild);
++nextLevel;
}
if (pNode->rightchild != nullptr)
{
nodes.push(pNode->rightchild);
++nextLevel;
}
nodes.pop();
--toBeprint;
if (toBeprint == 0)
{
printf("\n");
toBeprint = nextLevel;
nextLevel = 0;
}
}
}
2.3“之”字型打印二叉树
1、题目要求
实现一个函数按照“之”字型打印二叉树,具体的我们以下列这个二叉树为例来分析。

他的打印顺序就是
1
3,2
4,56,7
15,14,13,12,11,10,9,8
2、题目分析
我们还是以具体的例子来加以分析,还是和上面广度优先遍历类似,在打印结点1的时候需要一个容器来保存他的子结构,由于我们的打印顺序是3,2。所以是一种先进后出的结构,因此可以得出我们使用栈来保存子结构的值。此外,因为相邻两层的打印顺序是不同的,所以可以明确的说要使用两个栈,具体原因,我们来好好分析一下打印过程吧。
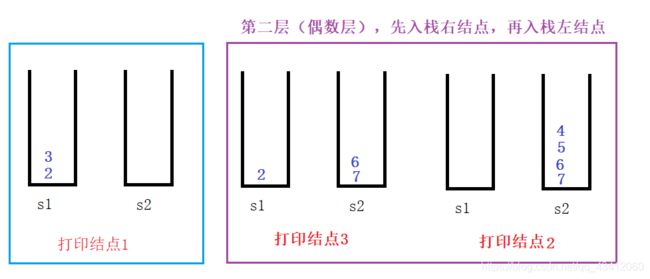
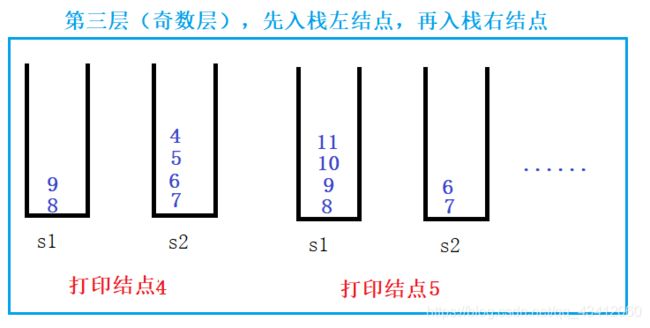
从上面的分析过程,我们就可以总结出入栈经验了。我们在打印一层结点的时候,把下一层结点存到相应的栈里面。如果打印的是奇数层,则先保存左子结构再保存右子结构;如果打印的是偶数层,则相反的操作。具体代码实现如下:
void Print(BinaryTreeNode* pRoot)
{
if (pRoot == nullptr)
return;
std::stack<BinaryTreeNode*>levels[2];
int current = 0;
int next = 1;
levels[current].push(pRoot);
while (!levels[0].empty() || levels[1].empty())
{
BinaryTreeNode* pNode = levels[current].top();
levels[current].pop();
printf("%d", pNode->m_data);
if (current == 0)
{
if (pNode->leftchild != nullptr)
levels[next].push(pNode->leftchild);
if (pNode->rightchild != nullptr)
levels[next].push(pNode->rightchild);
}
else
{
if (pNode->rightchild != nullptr)
levels[next].push(pNode->rightchild);
if (pNode->leftchild != nullptr)
levels[next].push(pNode->leftchild);
}
if (levels[current].empty())
{
printf("\n");
current = 1 - current;
next = 1 - next;
}
}
}
另外还有通过一个栈和一个队列的实现方式,具体参照博文二叉树遍历详解