机器学习之线性回归及梯度下降
备注:本文是整理了很多博客和Ng课程笔记以及自己的理解写的关于线性回归以及梯度下降算法的框架,力求简洁明了。
本文框架:
(1)线性回归的定义
(2)单变量线性回归
(3)代价函数cost function:评价线性回归是否拟合训练集的方法
(4)梯度下降:解决线性回归的方法之一
(5)特征缩放feature scaling:加快梯度下降执行速度的方法
(6)多变量线性回归
一.线性回归的定义
线性回归算法属于监督学习的一种,主要用于模型为连续函数的数值预测。
线性回归算法整体思路:
线性回归属于监督学习,因此方法和监督学习应该是一样的,
- 先给定一个训练集,
- 根据这个训练集学习出一个线性函数
- 然后测试这个函数训练的好不好(即此函数是否足够拟合训练集数据)
- 挑选出最好的函数(cost function最小)即可
(a) 根据给定数据架设预测函数h(x)
(b) 计算代价函数J
(c) 计算各参数偏导
(d) 更新参数
(e) 重复2~4直到代价函数跟新的步长小于设定值或者是重复次数达到预设值。
注意:
(1)因为是线性回归,所以学习到的函数为线性函数,即直线函数;
(2)因为是单变量,因此只有一个x;
二. 单变量线性回归
我们能够给出单变量线性回归的模型:
我们常称x为feature(特征),h(x)为hypothesis(假设函数);
从上面“方法”中,我们肯定有一个疑问,怎么样能够看出线性函数拟合的好不好呢?
我们需要使用到Cost Function(代价函数)
代价函数越小,说明线性回归地越好(和训练集拟合地越好),
当然最小就是0,即完全拟合;
举个实际的例子:
我们想要根据房子的大小,预测房子的价格,给定如下数据集:
根据以上的数据集画在图上,如下图所示:
我们需要根据这些点拟合出一条直线,使得cost Function最小;
虽然我们现在还不知道Cost Function内部到底是什么样的,但是我们的目标是:
给定输入向量x,输出向量y,theta向量
然后输出 Cost值;
以上我们对单变量线性回归的大致过程进行了描述;
三.代价函数cost function
Cost Function的用途:
对假设的函数进行评价,cost function越小的函数,说明拟合训练数据拟合的越好;
下图详细说明了当cost function为黑盒的时候,cost function 的作用;
但是我们肯定想知道cost Function的内部构造是什么?因此我们下面给出公式:
其中:
表示向量x中的第i个元素;
表示向量y中的第i个元素;
表示已知的假设函数;
m为训练集的数量;
比如给定数据集(1,1)、(2,2)、(3,3)
则x = [1;2;3],y = [1;2;3] (此处的语法为Octave语言的语法,表示3*1的矩阵)
如果我们预测theta0 = 0,theta1 = 1,
则h(x) = x
则cost function:
J(0,1) = 1/(2*3) * [(h(1)-1)^2+(h(2)-2)^2+(h(3)-3)^2] = 0;
如果我们预测theta0 = 0,theta1 = 0.5
则h(x) = 0.5x,
则cost function:
J(0,0.5) = 1/(2*3) * [(h(1)-1)^2+(h(2)-2)^2+(h(3)-3)^2] = 0.58;
如果theta0 一直为 0, 则theta1与J的函数为:
如果有theta0与theta1都不固定,则theta0、theta1、J 的函数为:![]()
当然我们也能够用二维的图来表示,即等高线图;
![]()
注意:如果是线性回归,则costfunctionJ与的函数一定是碗状的,即只有一个最小点;
以上我们讲解了cost function 的定义、公式;
四.梯度下降Gradient Descent
但是又一个问题引出了,虽然给定一个函数,我们能够根据cost function知道这个函数拟合的好不好,但是毕竟函数有这么多,总不可能一个一个试吧?
因此我们引出了梯度下降:能够找出cost function函数的最小值;
梯度下降原理:将函数比作一座山,我们站在某个山坡上,往四周看,从哪个方向向下走一小步,能够下降的最快;
当然解决问题的方法有很多,梯度下降只是其中一个,还有一种方法叫Normal Equation(正规方程);
方法:
(1)先确定向下一步的步伐大小,我们称为Learning rate;
(2)任意给定一个初始值:;
(3)确定一个向下的方向,并向下走预先规定的步伐,并更新;
(4)当下降的高度小于某个定义的值,则停止下降;
算法:
特点:
(1)初始点不同,获得的最小值也不同,因此梯度下降求得的只是局部最小值;
(2)越接近最小值时,下降速度越慢;
问题:如果初始值就在local minimum的位置,则会如何变化?
答:因为已经在local minimum位置,所以derivative(导数) 肯定是0,因此不会变化;
如果取到一个正确的值,则cost function应该越来越小;
问题:怎么取值?
答:随时观察值,如果cost function变小了,则ok,反之,则再取一个更小的值;
下图就详细的说明了梯度下降的过程:
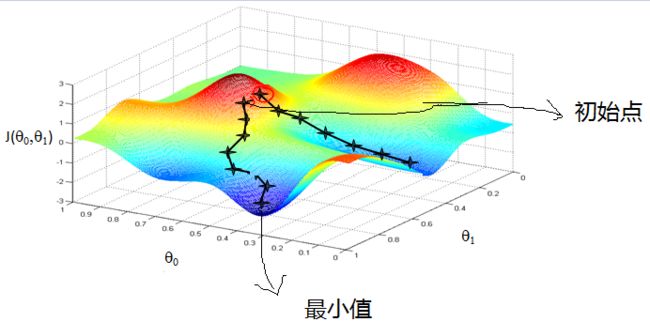
从上面的图可以看出:初始点不同,获得的最小值也不同,因此梯度下降求得的只是局部最小值;
注意:
下降的步伐大小非常重要,因为如果太小,则找到函数最小值的速度就很慢,如果太大,则可能会出现overshoot the minimum的现象;
下图就是overshoot minimum现象:
如果Learning rate取值后发现J function 增长了,则需要减小Learning rate的值;
单变量线性回归的梯度下降
线性回归需要使得cost function的最小;
因此我们能够对cost function运用梯度下降,即将梯度下降和线性回归进行整合,如下图所示:
上式中右边的公式推导过程如下:
![]()
梯度下降是通过不停的迭代,而我们比较关注迭代的次数,因为这关系到梯度下降的执行速度,为了减少迭代次数,因此引入了Feature Scaling;
五.特征缩放Feature Scaling
此种方法应用于梯度下降,为了加快梯度下降的执行速度;
思想:
将各个feature的值标准化,使得取值范围大致都在-1<=x<=1之间;
常用的方法是Mean Normalization(均值归一化),即
![]()
[X-mean(X)]/std(X)
mean(x):求平均值
std(x):求标准差
举个实际的例子,
有两个Feature:
(1)size,取值范围0~2000;
(2)#bedroom,取值范围0~5;
则通过feature scaling后
六.多变量线性回归
注意:多变量线性回归之前必须要Feature Scaling(特征缩放)!
前面我们只介绍了单变量的线性回归,即只有一个输入变量,现实世界不可能这么简单,因此此处我们要介绍多变量的线性回归;
举个例子:
房价其实由很多因素决定,比如size、number of bedrooms、number of floors、age of home等,这里我们假设房价由4个因素决定,如下图所示:
我们前面定义过单变量线性回归的模型:
这里我们可以定义出多变量线性回归的模型:
Cost function如下:
如果我们要用梯度下降解决多变量的线性回归,则我们还是可以用传统的梯度下降算法进行计算:
注意:这里有偏导数的推导问题,具体可以参考 单变量线性回归的梯度下降公式推导,虽然最后梯度下降的形式一样,但是它们的根本的预测函数h(x)不同。