KNN最近邻算法

1、最近邻算法

  最近邻算法是一种基于实例的学习，或者是局部近似和将所有计算推迟到分类之后的惰性学习，可以用于基本的分类与回归方法。

  如下图所示，最近邻算法的工作原理是存在一个样本数据集合，也称作训练样本集，并且样本集中每个数据都存在标签，即我们知道样本集中每一数据与所属分类的对应关系。输入没有标签的新数据后，将新数据的每个特征与样本集中数据对应的特征进行比较，然后算法提取样本集中特征最相似数据(最近邻)的分类标签。

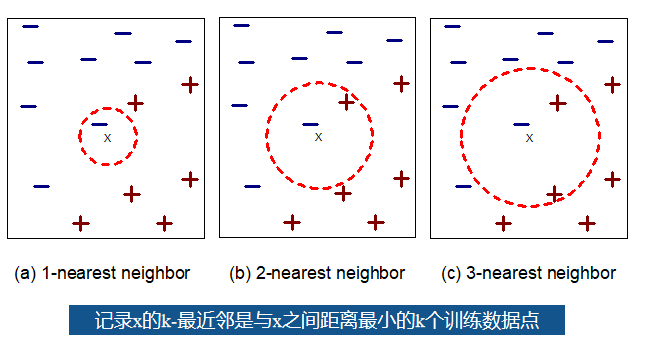
  最近邻分类器基本思想可以通俗地描述为“如果走的像鸭子，叫的像鸭子，看起来还像鸭子，那么它很可能就是一只鸭子”。最近邻算法要求存放训练记录，计算记录间举例地度量，并计算最近邻数k的值。对未知记录分类依靠计算域各个训练记录的距离，找出k个最近邻，使用最近邻的类标号决定位置记录的类标号(例如，多数表决)。

  在分类阶段，k是一个用户定义的常数。一个没有类别标签的向量(查询或测试点)将被归类为最接近该点的k个样本点中最频繁使用的一类。

2、距离度量方法

2.1 欧氏距离(Euclidean distance)

$$d(x,y)=\sqrt{\sum _i(x_i-y_i{)}^2}$$

  欧几里得度量（Euclidean Metric）（也称 欧氏距离）是一个通常采用的距离定义，指在维空间中两个点之间的真实距离，或者向量的自然长度（即该点到原点的距离）。 在二维和三维空间中的欧氏距离就是两点之间的实际距离。

2.2 曼哈顿距离(Manhattan distance)

$$d(x,y)=\sum _i|x_i-y_i|$$

  想象你在城市道路里，要从一个十字路口开车 到另外一个十字路口，驾驶距离是两点间的直线距离吗？显然不是，除非你能穿越大楼。实际驾驶距离就是这个“曼哈顿距离” 。而这也是曼哈顿距离名称的来源， 曼哈顿距离也称为城市街区距离(City Block distance)。

2.3 切比雪夫距离(Chebyshev distance)

$$d(x,y)=ma{x}_i|x_i-y_i|$$

  二个点之间的距离定义是其各坐标数值差绝对值的最大值。

  国际象棋棋盘上二个位置间的切比雪夫距离是 指王要从一个位子移至另一个位子需要走的步数。由于王可以往斜前或斜后方向移动一格， 因此可以较有效率的到达目的的格子。下图是棋盘上所有位置距f6位置的切比雪夫距离。

2.4 闵可夫斯基距离(Minkowski distance)

$$d(x,y)=(\sum _i|x_i-y_i{|}^p{)}^{\frac{1}{p}}$$

取1或2时的闵氏距离是最为常用的:

• = 2即为欧氏距离，
• = 1时则为曼哈顿距离
• 当取无穷时的极限情况下，可以得到切比雪 夫距离

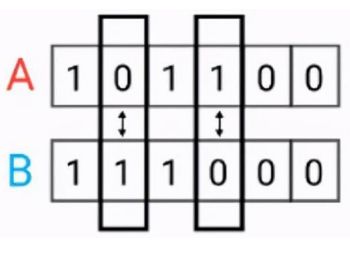
2.5 汉明距离(Hamming distance)

$$d(x,y)=\frac{1}{N}\sum _i{1}_{x_i\ne y_i}$$

  汉明距离是使用在数据传输差错控制编码里面的，汉明距离是一个概念，它表示两个（ 相同长度）字对应位不同的数量，我们以表示两个字之间的汉明距离。对两个字符串进行异或运算，并统计结果为1的个数，那么这个数就是汉明距离。

2.6 余弦相似度

  两个向量有相同的指向时，余弦相似度的值为1；两 个向量夹角为90°时，余弦相似度的值为0；两个向 量指向完全相反的方向时，余弦相似度的值为-1。

  假定和是两个维向量，是 $[A_1,A_2,...,A_n]$ ，是 $[B_1,B_2,...,B_n]$，则和的夹角的余弦等于：
$$\cos (\theta )=\frac{A\cdot B}{\Vert A\Vert \Vert B\Vert }=\frac{{\sum }_{i=1}^n{A}_i\times B_i}{\sqrt{{\sum }_{i=1}^n(A_i{)}^2}\times \sqrt{{\sum }_{i=1}^n(B_i{)}^2}}$$

  一般情况下，将欧氏距离作为距离度量，但是这只适用于连续变量。在文本分类这种离散变量情况下，可以用汉明举例作为度量。如下图所示，对于基因表达微阵列数据，KNN也可以与Pearson和Spearman相关系数结合使用。通常情况下，如果运用一些特殊的算法来计算度量的话，k近邻分类精度可显著提高，如运用大间隔最近邻居或者邻里成分分析法。

3、kNN算法流程

算法流程如下：

• 1.计算测试对象到训练集中每个对象的距离

• 2.按照距离的远近排序

• 3.选取与当前测试对象最近的k的训练对象， 作为该测试对象的邻居

• 4.统计这k个邻居的类别频次

• 5.k个邻居里频次最高的类别，即为测试对象 的类别

4、KNN算法特点

• 是一种基于实例的学习

  • 需要一个邻近性度量来确定实例间的相似性或距离

• 不需要建立模型，但分类一个测试样例开销很大

  • 需要计算域所有训练实例之间的距离

• 基于局部信息进行预测，对噪声非常敏感

• 最近邻分类器可以生成任意形状的决策边界

  • 决策树和基于规则的分类器通常是直线决策边界

• 需要适当的邻近性度量和数据预处理

  • 防止邻近性度量被某个属性左右

5、使用KNN实现鸢尾花数据集分类

#  knn实现鸢尾花数据集分类
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split
import numpy as np
import pandas as pd


data_url = "Iris.csv"
df = pd.read_csv(data_url)
X = df.iloc[:, 1:5]
y = df.iloc[:, 5]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

# 利用KNeighborsClassifier函数制作knn分类器
# 选取最近的点的个数n_neighbors=3
###########Begin###########

clf = KNeighborsClassifier(n_neighbors=6)

###########End#############
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
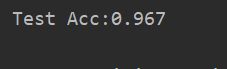
acc = np.sum(y_test == y_pred) / X_test.shape[0]
print("Test Acc:%.3f" % acc)