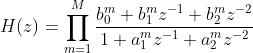IIR滤波器设计基础及Matlab设计示例

目录

1. 概要

2. IIR 和 FIR 滤波器的定义

3. IIR滤波器和FIR滤波器的优缺点对比

4. 双二次（Biquad）IIR 滤波器

5. IIR滤波器设计指标（specifications）

5.1 滤波器的频率响应特性

5.2 模拟滤波器类型

5.3 IIR滤波器结构

5.3.1 Direct Form IIR structure

5.3.2 Direct Form I IIR structure

5.3.3 Direct Form II IIR structure

6. 基于Matlab的SOS IIR滤波器设计例

---

1. 概要

        本文概要性地介绍IIR滤波器设计的基础知识，以及基于Matlab进行IIR滤波器设计的示例。

2. IIR 和 FIR 滤波器的定义

        数字滤波器，顾名思义，是一种离散时间系统（ discrete-time systems），用于对采样信号进行算法性的处理，以改变（比如说减弱或者增强等）输入信号中某种特定的属性。

        比如说，从频域的角度来看，数字滤波器可以用来使得输入信号的某些频率范围的分量通过，而使得另外一些频率范围的分量被阻塞（衰减），或者使得某些频率范围的信号的相位发生所希望的改变。 

        从时域的角度来看，数字滤波器对于输入信号中的动态变化的响应可以用系统冲激响应来表征。在频域中，滤波器的特性则由系统传递函数（transfer function of the system）来刻画。

       冲激响应（impulse response）总是一个无限长度的实现信号序列，其中，每个（采样）时刻的值可以是零也可以是非零。数字滤波器的冲激响应中的非零值通常被称为抽头（Taps）。根据冲激响应中抽头数（即非零值的个数）是有限的还是无限的，数字滤波器可以分为两类：无限冲激响应（Infinite Impulse Response ：IIR) 滤波器；有限冲激响应（Finite Impulse Response ：FIR) 滤波器。

        IIR滤波器的冲激响应中包含无限个非零值，而FIR滤波器的冲激响应中只包含有限个非零值。

        注：以上仅为一种看待数字滤波器分类的观点。另一种等价的观点是看冲激响应的非零区间的覆盖范围（英文文献中常用support这个词来表示）是有限长的还是无限长的。 

        从结构上看，IIR滤波器和FIR滤波器有一个显著的差异就是IIR滤波器有反馈部分，而FIR滤波器没有反馈部分。       

3. IIR滤波器和FIR滤波器的优缺点对比

        当需要设计一个数字滤波器时，需要在IIR滤波器和FIR滤波器两种类型之间进行折衷考虑，在能够满足系统设计需求的前提条件下在实现代价、稳定性等方面取得最好的折衷。以下列举IIR滤波器的优缺点，显而易见的是它们分别对应FIR滤波器的缺点和优点。

        IIR Advantages：

•         • 获取等价的特性的前提下，IIR滤波器的运算负荷更低。更通俗一点说就是IIR所需要的抽头数更少
  •         • IIR滤波器的处理延迟（更正式的提法是群时延 group delay）更低（这个当然也是与抽头数少直接相关联的）

        IIR Disadvantages：

•         • 系统稳定性更难以保证。但是通过仔细的选择零点和极点的位置及搭配可以有效地缓解这个问题，滤波器设计工具可以提供关于零极点选择的有效帮助。与之相对，FIR滤波器是无条件稳定的。
  •         • 系统的相位响应更难以控制。FIR滤波器通过采用具有对称性的抽头设计可以获得线性相位响应，但是IIR则比较难以控制其相位响应，更不用谈什么线性相位响应。
    •         • 对数值计算的误差更加敏感。数字滤波器通常在某种形式的计算机中执行运算，其数值表示精度是有限的（即便浮点运算也是有限精度的），有限精度就必然带来运算误差，而IIR滤波器由于其存在反馈路径使得误差会累积传递，所以相比FIR滤波器更加容易受到有限精度运算的影响。
      •         • IIR滤波器设计的数学流程更加复杂、模糊。与之相对的是，FIR滤波器设计存在确定性的最优的设计流程。所幸的是像Matlab、Pyton Scipy等都提供了优良的滤波器设计工具缓解了这一问题。

4. 双二次（Biquad）IIR 滤波器

        如前所述，数字滤波器的在频域上的响应可以由它的传递函数（transfer function）来刻画。IIR滤波器的传递函数表示为一个z变换分式，其中分子对应于IIR滤波器的前向（feed-forward）部分，包含了系统的零点（zeros）；分母对应于IIR滤波器的反馈（feedback）部分，包含了系统的极点（poles）。IIR的极点的个数表示滤波器的阶数（order），零、极点的位置则决定了系统的频率响应。注意：FIR的传递函数没有分母（或者说分母为1）,因此其阶数由零点的个数（或者更直观地说表示传递函数的多项式的阶数）决定。但是对于IIR滤波器来说，如果分子多项式的阶数高于分母多项式的阶数时，总是可以将其进行分解成两部分的级联，其中一部分是分子多项式的阶数不高于分母多项式的阶数的IIR滤波器，另部分则仅包含单纯的延时处理。因此我们可以将IIR滤波器的讨论仅限于其传递函数的分子多项式的阶数不高于分母多项式的阶数的情况。

        双二次IIR滤波器（biquadractic, biquad）是指传递函数的分子和分母都是二次多项式的IIR滤波器，因此有两个零点和两个极点。在实际应用中，通常需要高阶的IIR滤波器以获得足够陡峭的频域响应，但是，如前所述，IIR滤波器的数值稳定性不好，而且随着滤波器阶数变高愈加严重， 因此一个作为de facto standard的做法是将高阶IIR的传递函数分解为若干个双二次传递函数，以级联的方式来实现，这种用双二次IIR滤波器级联的方式实现高阶IIR滤波器的实现结构通常也称为SOS（series of cascaded Second-Order Sections）滤波器。

5. IIR滤波器设计指标（specifications）

        IIR滤波器设计指标（设计要求）通常从以下几个方面来定义：

•         1. 频率响应特性
  •         2. 模拟滤波器模板
    •         3. 结构 structure

5.1 滤波器的频率响应特性

        常见的滤波器的幅频响应有以下四类（本文不讨论如全通滤波器希尔伯特滤波器等之类的特殊滤波器）：低通滤波器；高通滤波器；带通滤波器；带阻滤波器。四种幅频响应特性分别如下图所示。其中带通滤波器和带阻滤波器均可以由一个低通滤波器和一个高通滤波器的级联而得。

图1. 四种幅频响应特性

        由于IIR滤波器通常不具有线性相位，因此其应用场景也通常就是不要求相位响应的地方。因此IIR滤波器的频率响应指标定义通常都只关注幅频响应。

        确定了以上幅频响应类型后，相应地需要确定通带带宽及起止频率、阻带衰减、通带波纹等指标要求。

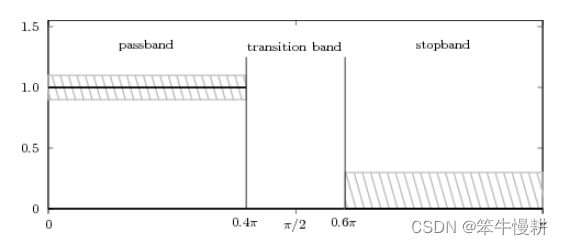
        以一个低通滤波器的设计要求为例，其设计指标要求可以表示为如下图所示：

图2 典型的低通滤波器设计指标要求

以下三图则分别是满足（最后一种）和不满足（前两种）以上要求的几种情况。 

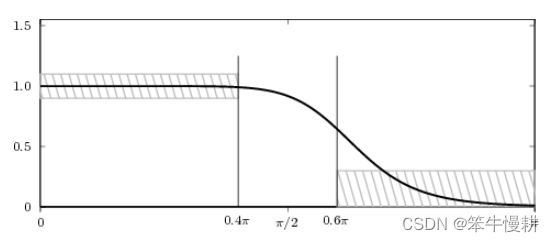
图2-1 不满足设计要求的例子（阻带衰减有一部分不满足） 

 

图2-2 不满足设计要求的例子（通带波纹不满足）  

 

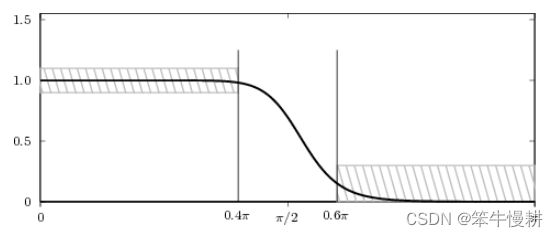
图2-3 满足（甚至是超过了）设计要求的例子

5.2 模拟滤波器类型

        IIR滤波器设计不像FIR滤波器设计那样有成熟的优化算法流程可用，所以通常采取参考模拟滤波器模板的设计流程的方式进行，通过调整模拟滤波器参数值的方式来满足所需要的幅度和相位特性。Matlab等信号处理工具提供了很好的设计IIR滤波器的工具。 通常来说，基于Matlab设计IIR滤波器的第一步就是先确定模拟滤波器模板类型。

        常见的模拟滤波器有以下4种类型。

巴特沃斯（Butterworth）滤波器，其主要特性如下： 

        • 通带和阻带没有波纹（ripple）

        • 通带到阻带的滚降（roll-off）最平缓（换言之，过渡带不陡峭）

        • 相位失真适中

切比雪夫I型（Chebyshev I）滤波器，其主要特性如下：

        • 通带有波纹（Ripple），阻带平坦（无波纹）

        • 过渡带滚降特性比巴特沃斯滤波器要陡峭

        • 群时延特性较差，即相位失真比巴特沃斯严重

切比雪夫II型（Chebyshev II, Inverse Chebyshev I）滤波器 ，其主要特性如下：

        • 通带平坦（无波纹），阻带有波纹

        • 过渡带滚降特性介乎于巴特沃斯滤波器与切比雪夫II型之间

椭圆型（Elliptical）滤波器，其主要特性如下：

        • 通带和阻带都有波纹

        • 过渡带滚降特性是（这四种之中）最陡峭的

        以下图中显示了以上四种低通模拟滤波器的频域响应（假定相同的带宽和阻带衰减等设计指标，with the same specifications）。注意这些滤波器在通带、阻带波纹以及过渡带陡峭度方面的差异对比。

图3 相同设计指标条件下四种模拟滤波器的频率响应的对比

5.3 IIR滤波器结构

        如上所述，IIR滤波器的传递函数可以表示为以下通用形式（多个二阶滤波器的传递函数的乘积对应于多个Biquad滤波器的级联，其中最多可能有一个是退化成一阶的传递函数）：

                
 

        分子包含的是前向路径的参数，分母包含的反馈路径的参数。每个Biquad IIR滤波器对应的差分方程如下所示：

                

5.3.1 Direct Form IIR structure

        一种直观的IIR滤波器的差分方程的实现结构如下所示，这种结构被称为Direct Form结构。

图4 Direct Form structure of an IIR filter. 

5.3.2 Direct Form I IIR structure

        IIR滤波器的前馈（feed-forward）部分和反馈（feedback）部分的处理是顺序可交换的，将Direct Form的结构中前馈部分和反馈部分顺序交换一下即可得到如下结构：

图5  Direct Form I structure 

        乍一看，这种交换似乎并没有什么好处。但是，仔细一看可以发现现在排在中间的两排延迟链是重复的，因此是可以融合到一起的，由此我们可以得到Direct Form II结构如下所示。

5.3.3 Direct Form II IIR structure

 图6  Direct Form II structure 

        这种结构的特征是延迟单元使用量最少（ the minimum number of delay elements），因而也就称为最常用的IIR滤波器实现结构。

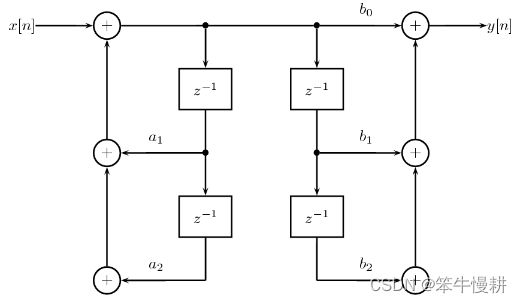
        通过将图6这种结构级联起来就可以得到更高阶的传递函数的实现，如下图所示：

        Direct Form 2 转置结构的Biquad级联IIR滤波器如下图所示。       

                        图7. Direct Form 2 转置结构的Biquad级联IIR（SOS）滤波器  

 

6. 基于Matlab的SOS IIR滤波器设计例

        如前所述，IIR滤波器的设计通常是从根据设计需求选择一个模拟滤波器原型模板（这个更多地需要依靠经验），当确定了模拟滤波器原型模板，就可以利用Matlab提供的工具来计算出所选定的模拟滤波器的离散版本的传递函数。然后可以利用sos()函数或者tf2sos()函数将这个传递函数分解为biquad级联的形式，也即SOS形式。如以下代码所示（以一个巴特沃斯滤波器的离散版为例）：

N = 10;
Fc = 0.4;
[b,a] = butter(N,Fc);

% Create a dsp.IIRFilter object and assign the designed coefficients to the Numerator and the Denominator properties of the object.

iir = dsp.IIRFilter('Numerator',b,'Denominator',a)

% Use the sos function to convert the IIR filter object into a biquadratic filter that contains the corresponding SOS sections.

biquad = sos(iir)

% You can access the SOS matrix and the scale value properties of the biquadratic filter.

sMatrix = biquad.SOSMatrix
sValues = biquad.ScaleValues

% To verify, compare these values to the values obtained using the tf2sos function.
[sMatrix2,g] = tf2sos(b,a)
isequal(sMatrix,sMatrix2)
isequal(sValues(1),g)

        除了butter()以外，还有cheby1(), cheby2(),ellip()分别用于设计前面提到的几种经典的模拟滤波器的对应的离散版本IIR滤波器的传递函数。 这些函数都有一个参数指定是设计低通特性还是高通特性。如下例所示。

        生成了sos matrix以后，可以直接调用sosfilt()函数以sos matrix为参数对输入数据进行滤波。

load chirp.mat         % 加载chirp数据。这是matlab内置的例子数据。
t = (0:length(y)-1)/Fs;
[zhi,phi,khi] = butter(7,0.48,'high'); % 'high'参数指定生成高通滤波器
soshi = zp2sos(zhi,phi,khi);
freqz(soshi)
outhi = sosfilt(soshi,y); %利用所生成的sos矩阵，调用sosfilt()进行滤波

figure
subplot(2,1,1)
plot(t,y)
title('Original Signal')
ys = ylim;

subplot(2,1,2)
plot(t,outhi)
title('Highpass-Filtered Signal')
xlabel('Time (s)')
ylim(ys)

        高通滤波器的效果如下，肉眼看不出什么太大的差异。这个不足为奇，因为chirp信号本来就主要是由高频成分构成。 

 

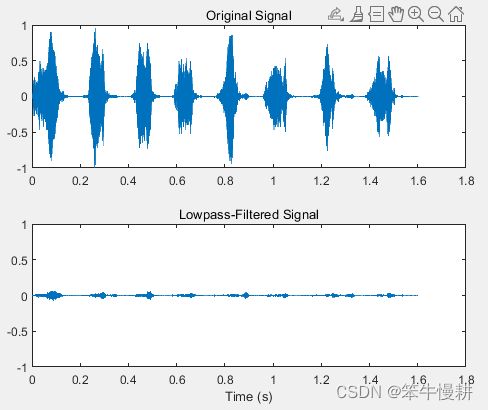
        以下为低通滤波示例。

[zlo,plo,klo] = butter(7,0.48); % 没有指定类型参数，缺省为低通滤波器
soslo = zp2sos(zlo,plo,klo);

outlo = sosfilt(soslo,y);

subplot(2,1,1)
plot(t,y)
title('Original Signal')
ys = ylim;

subplot(2,1,2)
plot(t,outlo)
title('Lowpass-Filtered Signal')
xlabel('Time (s)')
ylim(ys)

 

        可以看出，经过低通滤波后，几乎没有剩下什么了。从另一个角度印证了chirp信号主要由高频成分构成，低频成分基本上都是噪声了。

 

参考文献：

【1】Signal Processing for Communications (sp4comm.org)