Batch Normalization详解（原理+实验分析）
Batch Normalization详解（原理+实验分析）
- 1. 计算过程
- 2. 前向传播过程
- 3. 反向传播过程
- 4. 实验分析
-
- 4.1 实验一：验证有没有BatchNorm下准确率的区别
- 4.2 实验二：验证有没有BatchNorm+noisy下准确率的区别
- 4.3 实验三：验证有没有BatchNorm+noisy下准确率的区别
- 4.4 实验小结
- 5. BatchNorm的其他细节
-
- 5.1 训练和推理阶段时参数的初始化问题
- 5.2 BatchNorm在哪个位置最好？
- 5.3 在训练时为什么不直接使用整个训练集的均值/方差？
- 5.4 在预测时为什么不直接使用整个训练集的均值/方差？
- 5.5 batch_size的配置
- 5.6 对学习率有何影响？
- 5.7 BN是正则化吗？
- 5.8 与Dropout的有何异同？
- 5.9 能否和Dropout混合使用？
- 5.10 BN可以用在哪些类型的网络？
- 5.11 缺点
注：本文内容和我的另一篇博客：，在内容上有些重合。本文前三节都是一些表面的东西，第四节注重BN本身的意义和问题，即实验分析，建议重点放在第四节。
1. 计算过程
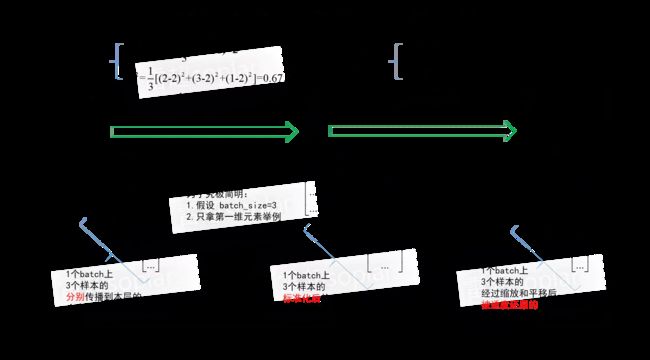
简单地说，就是在batch的维度上计算相同通道上的均值和方差；然后再用相同batch维度上的均值和方差来做标准化。具体计算过程演示图如下：
认真看应该会看明白吧，看不懂的欢迎下面留言提问。
2. 前向传播过程
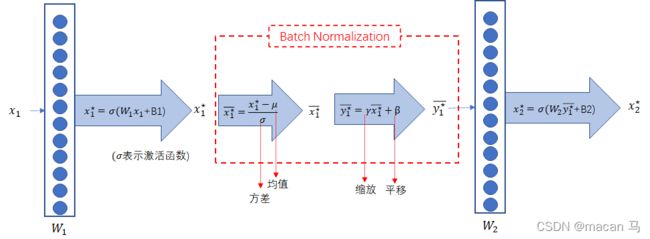
未加入Normalization之前的神经网络长成这样：
就是简单的两层全连接，中间有一个激活函数，没啥好说的。
加入BN后前向传播长成这样：
就是在激活函数之后，计算均值和方差做标准化，然后使用 γ \gamma γ做缩放， β \beta β做平移（初始化为1、0）。
均值和方差比较好理解，但是缩放系数 γ \gamma γ和平移系数 β \beta β具体有什么意义呢？
由标准化公式 x i ^ = x i − μ σ 2 + ϵ \hat{x_{i}}=\frac{x_{i}-\mu}{\sqrt{\sigma^{2}+\epsilon}} xi^=σ2+ϵxi−μ，可变换下得到：
x i = σ x i ^ + μ (1) x_{i}=\sigma \hat{x_{i}}+\mu \tag{1} xi=σxi^+μ(1)
再看下还原公式：
y i = γ x i ^ + β (2) y_{i}=\gamma \hat{x_{i}}+\beta \tag{2} yi=γxi^+β(2)
(2)中 γ \gamma γ和 β \beta β都是向量，显然 γ \gamma γ是对 x i ^ \hat{x_{i}} xi^的缩放， β \beta β 是对 γ x i ^ \gamma\hat{x_{i}} γxi^的平移。可以增加可学习的参数 γ \gamma γ、 β \beta β，如果 γ = σ \gamma=\sigma γ=σ, β = μ \beta = \mu β=μ，则 y i = x i y_{i}=x_{i} yi=xi，即可以完全还原到未normalization之前的输入！
我们可以通过反向传播来训练这两个参数（推导表明这是可以训练的），而至于 γ \gamma γ 多大程度上接近 σ \sigma σ , β \beta β 多大程度上接近 μ \mu μ ,让损失函数对它们计算出的梯度决定！
另外贴一张别人写的计算BN的例子：
3. 反向传播过程
前向传播很好理解，反向传播就比较复杂，这块要是掰开了揉碎了说的话，又会占用大量的篇幅，所以我在我的另一篇博客：Batch Normalization的反向传播解说详细说明了BN的反向传播，欢迎关注、评论转发。
4. 实验分析
本文中涉及到的实验数据及分析，均来自于论文《How Does Batch Normalization Help Optimization?
》
4.1 实验一：验证有没有BatchNorm下准确率的区别
实验设置：
· 任务：分类
· 数据集：CIFAR-10
· backbone：VGG
· 对比条件：两个变量，即有没有使用BatchNorm和学习率
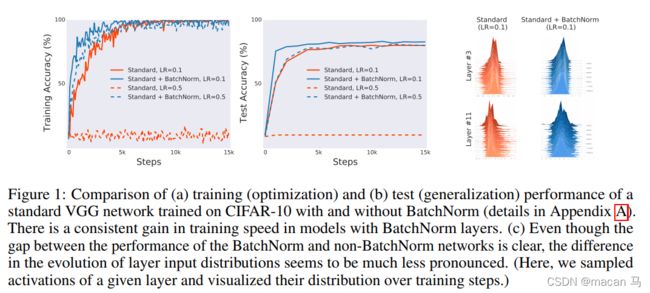
分析：
- 不同点：
· a. 图一中表明，在训练时，使用BatchNorm会比不使用更快的进入到收敛状态
· b. 图二中表明，在测试时，使用BatchNorm会比不使用达到更高的准确率- 相同点：
· c. 图三中表明，使用和不使用BatchNorm，在特征权重分布上的差异不明显
针对上述的c点，不禁让我们怀疑了，BatchNorm对分布约束是否有作用？下面用实验二来验证。
4.2 实验二：验证有没有BatchNorm+noisy下准确率的区别
实验设置：
· 任务：分类
· 数据集：CIFAR-10
· backbone：VGG
· 对比条件：两个变量，即有没有使用BatchNorm和随机噪声
分析：
- 不同点：
· a. 图一中表明，在训练时，使用BatchNorm会比不使用更快的进入到收敛状态
· b. 图一中表明，在训练时，即使存在噪声，使用BatchNorm也会比不使用更快的进入到收敛状态
· c. 图二中表明，添加噪声后的模型的某一层的分布，会比不使用BatchNorm和没有噪声的BatchNorm的稳定性更差- 相同点：
· d. 图一中表明，添加的噪声的模型，在有BatchNorm的作用下，噪声对模型的影响十分的小
显然，这些发现很难与BatchNorm带来的性能提升源于层输入分布稳定性增加的说法相一致，所以下面进行实验三。
4.3 实验三：验证有没有BatchNorm+noisy下准确率的区别
根据上图，概括性地说，BatchNorm改善了损失的平滑性，使得损失函数曲面变得平滑，而平滑的损失函数进行梯度下降法变得非常容易。（“平滑性”参考下图） 
4.4 实验小结
为什么BatchNorm会好使？从上面的三个实验可以看出，其原因并不主要是因为对分布有了较稳定的约束能力，更主要的原因是BatchNorm改善了损失的平滑性！
5. BatchNorm的其他细节
5.1 训练和推理阶段时参数的初始化问题
在训练阶段， 均值 μ \mu μ和方差 σ \sigma σ不用初始化，是计算出来的；缩放系数 γ \gamma γ和 β \beta β分别初始化为1和0，训练阶段结束，模型会学习出 γ \gamma γ和 β \beta β作为推理阶段的初始化。
在推理阶段， 缩放系数 γ \gamma γ和 β \beta β分别初始化训练阶段学习到的值；均值 μ \mu μ和方差 σ \sigma σ利用训练集统计的均值和方差，统计方式一般包括移动平均和全局平均。（即在训练的时候实现计算好 mean 和 var 测试的时候直接拿来用就可以了，不用计算均值和方差。）
计算方法见我的另一篇博客：BatchNorm怎样解决训练和推理时batch size 不同的问题？
5.2 BatchNorm在哪个位置最好？
首先，由3中的反向传播可以知道，BatchNorm放在任何位置都能进行求导，所以BatchNorm放在哪里都行。
放在哪里最好？这个问题已经有大量的文论说明了，看论文吧（后续整理）
5.3 在训练时为什么不直接使用整个训练集的均值/方差？
使用 BN 的目的就是为了保证每批数据的分布稳定，使用全局统计量反而违背了这个初衷。
5.4 在预测时为什么不直接使用整个训练集的均值/方差？
完全可以。由于神经网络的训练数据量一般很大，所以内存装不下，因此用指数滑动平均方法去近似值，好处是不占内存，计算方便，但其结果不如整个训练集的均值/方差那么准确。
5.5 batch_size的配置
不适合batch_size较小的学习任务。因为batch_size太小，每一个step里前向计算中所统计的本batch上的方差和均值，噪音声量大，与总体方差和总体均值相差太大。前向计算已经不准了，反向传播的误差就更大了
5.6 对学习率有何影响？
由于BN对损失函数的平滑作用，因此可以采用较大的学习率。
5.7 BN是正则化吗？
在深度学习中，正则化一般是指为避免过拟合而限制模型参数规模的做法。即正则化=简化。BN能够平滑损失函数的曲面，显然属于正则化。不过，除了在过拟合时起正则作用，在欠拟合状况下，BN也能提升收敛速度。
5.8 与Dropout的有何异同？
BN由于平滑了损失函数的梯度函数，不仅使得模型训练精度提升了，而且收敛速度也提升了；Dropout是一种集成策略，只能提升模型训练精度。因此BN更受欢迎。
5.9 能否和Dropout混合使用？
虽然混合使用较麻烦，但是可以。不过现在主流模型已经全面倒戈BN。Dropout之前最常用的场合是全连接层，也被全局池化日渐取代
5.10 BN可以用在哪些类型的网络？
其他的都行，RNN网络不ok，因为无论训练和测试阶段，每个batch上的输入序列的长度都不确定，均值和方差的统计非常困难。
5.11 缺点
模型运行时间长