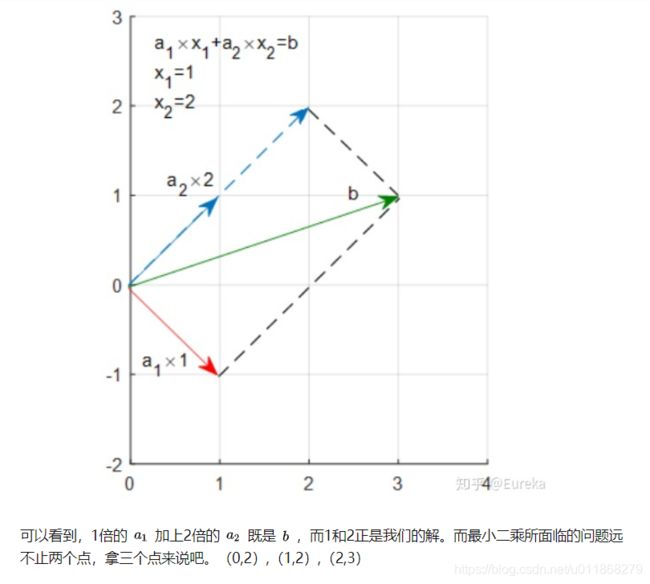
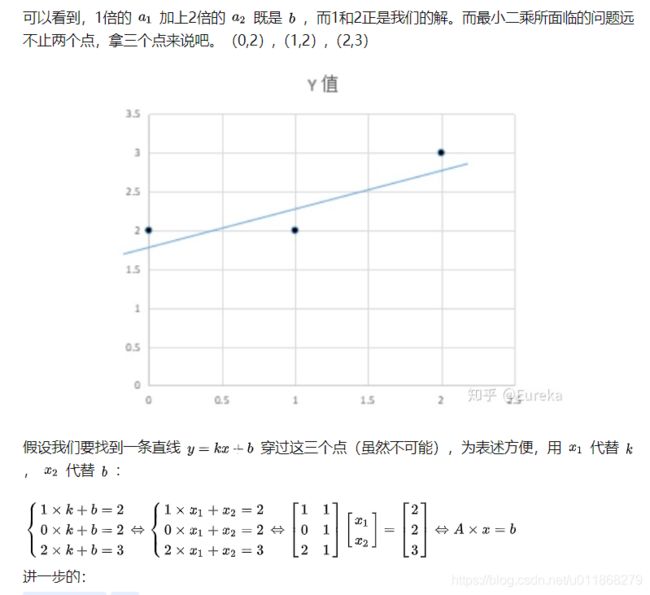
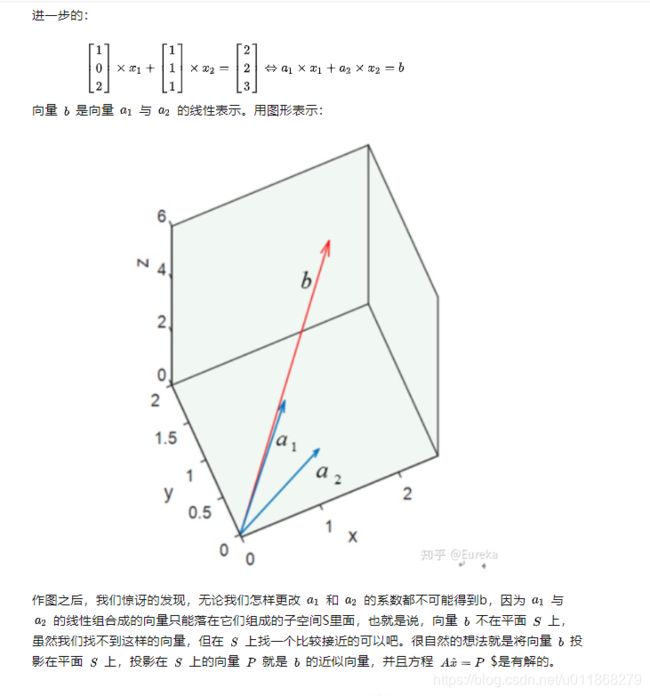
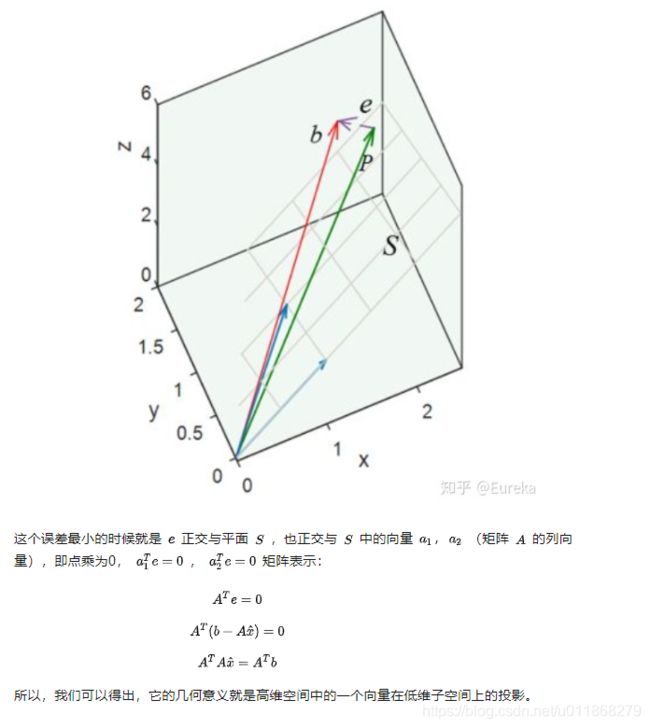
关于最小二乘法详解

最小二乘法的原理与要解决的问题

 

最小二乘法的矩阵法解法

 

最小二乘法的几何解释

 

最小二乘法的局限性和适用场景　

最小二乘法的python实战

 

import numpy as np

import scipy as sp

from scipy.optimize import leastsq

import matplotlib.pyplot as plt

%matplotlib inline

 

# 目标函数

def real_func(x):

    return np.sin(2*np.pi*x)

​

#多项式

#ps: numpy.polyld([1,2,3]) 生成  $1x^2+2x^1+3x^0$*

def fit_func(p, x):

    f = np.poly1d(p)

    return f(x)

​

# 残差

def residuals_func(p, x, y):

    ret = fit_func(p, x) - y

    return ret

​

 

# 十个点

x = np.linspace(0, 1, 10)

x_points = np.linspace(0, 1, 1000)

# 加上正态分布噪音的目标函数的值

y_ = real_func(x)

y = [np.random.normal(0, 0.1)+y1 for y1 in y_]

​

def fitting(M=0):

    """

    n 为 多项式的次数

    """    

    # 随机初始化多项式参数

    p_init = np.random.rand(M+1)

    # 最小二乘法

    p_lsq = leastsq(residuals_func, p_init, args=(x, y))

    print('Fitting Parameters:', p_lsq[0])

​

    # 可视化

    plt.plot(x_points, real_func(x_points), label='real')

    plt.plot(x_points, fit_func(p_lsq[0], x_points), label='fitted curve')

    plt.plot(x, y, 'bo', label='noise')

    plt.legend()

    return p_lsq

​

 

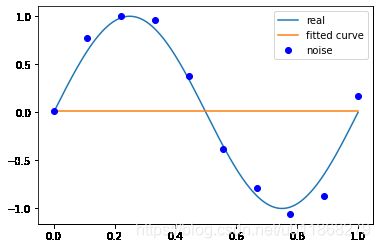
# M=0

p_lsq_0 = fitting(M=0)

Fitting Parameters: [0.01914362]

 

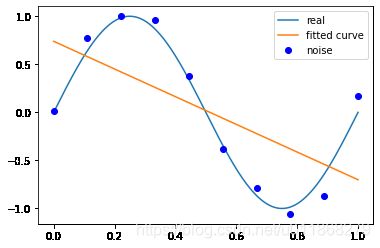
# M=1

p_lsq_1 = fitting(M=1)

Fitting Parameters: [-1.44035975  0.73932349]

 

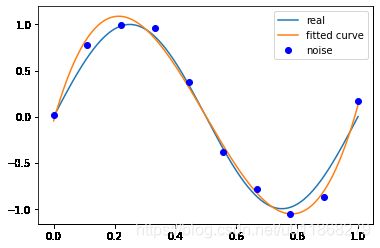
# M=3

p_lsq_3 = fitting(M=3)

Fitting Parameters: [ 23.32730356 -34.84982011  11.69490865  -0.04614352]

 

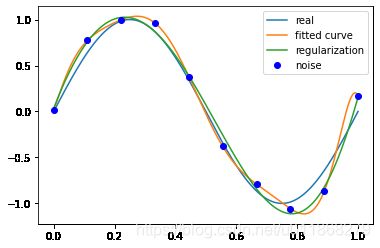
# M=9

p_lsq_9 = fitting(M=9)

Fitting Parameters: [-7.72885226e+03  3.20354672e+04 -5.42647096e+04  4.81881349e+04
 -2.38777532e+04  6.47385739e+03 -8.52906000e+02  1.74436725e+01
  9.47089325e+00  1.35011754e-02]

 

当M=9时，多项式曲线通过了每个数据点，但是造成了过拟合

正则化

结果显示过拟合， 引入正则化项(regularizer)，降低过拟合

[公式]

回归问题中，损失函数是平方损失，正则化可以是参数向量的L2范数,也可以是L1范数。

L1: regularization*abs(p) L2: 0.5 * regularization * np.square(p)

 

regularization = 0.0001

​

def residuals_func_regularization(p, x, y):

    ret = fit_func(p, x) - y

    ret = np.append(ret, np.sqrt(0.5*regularization*np.square(p))) # L2范数作为正则化项

    return ret

 

# 最小二乘法,加正则化项

p_init = np.random.rand(9+1)

p_lsq_regularization = leastsq(residuals_func_regularization, p_init, args=(x, y))

 

plt.plot(x_points, real_func(x_points), label='real')

plt.plot(x_points, fit_func(p_lsq_9[0], x_points), label='fitted curve')

plt.plot(x_points, fit_func(p_lsq_regularization[0], x_points), label='regularization')

plt.plot(x, y, 'bo', label='noise')

plt.legend()