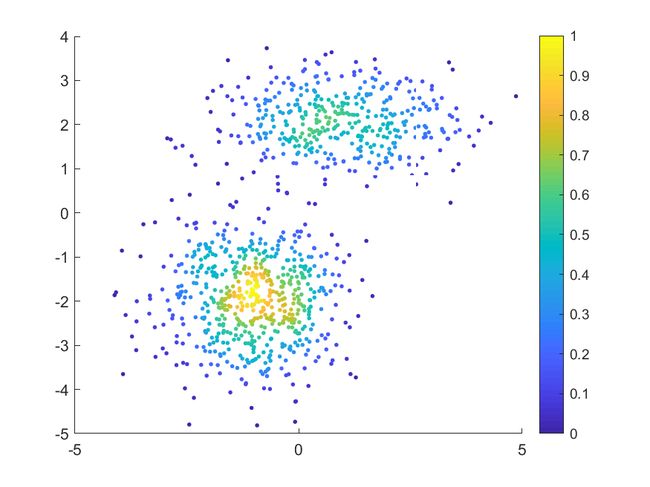
密度符号在matlab中,MATLAB实例：散点密度图

MATLAB实例：散点密度图

MATLAB绘制用颜色表示数据密度的散点图

1. demo.m

% 用颜色表示数据密度的散点图

data_load=dlmread('E:\scanplot\gauss.txt');

X=data_load(:,1:2);

scatplot(X(:,1),X(:,2),'circles', sqrt((range(X(:, 1))/30)^2 + (range(X(:,2))/30)^2), 100, 5, 1, 8);

% colormap jet

print(gcf,'-dpng','散点密度图.png');

2. scatplot.m

function out = scatplot(x,y,method,radius,N,n,po,ms)

% Scatter plot with color indicating data density

% https://www.mathworks.com/matlabcentral/fileexchange/8577-scatplot

% USAGE:

% out = scatplot(x,y,method,radius,N,n,po,ms)

% out = scatplot(x,y,dd)

%

% DESCRIPTION:

% Draws a scatter plot with a colorscale

% representing the data density computed

% using three methods

%

% INPUT VARIABLES:

% x,y - are the data points

% method - is the method used to calculate data densities:

% 'circles' - uses circles with a determined area

% centered at each data point

% 'squares' - uses squares with a determined area

% centered at each data point

% 'voronoi' - uses voronoi cells to determin data densities

% default method is 'voronoi'

% radius - is the radius used for the circles or squares

% used to calculate the data densities if

% (Note: only used in methods 'circles' and 'squares'

% default radius is sqrt((range(x)/30)^2 + (range(y)/30)^2)

% N - is the size of the square mesh (N x N) used to

% filter and calculate contours

% default is 100

% n - is the number of coeficients used in the 2-D

% running mean filter

% default is 5

% (Note: if n is length(2), n(2) is tjhe number of

% of times the filter is applied)

% po - plot options:

% 0 - No plot

% 1 - plots only colored data points (filtered)

% 2 - plots colored data points and contours (filtered)

% 3 - plots only colored data points (unfiltered)

% 4 - plots colored data points and contours (unfiltered)

% default is 1

% ms - uses this marker size for filled circles

% default is 4

%

% OUTPUT VARIABLE:

% out - structure array that contains the following fields:

% dd - unfiltered data densities at (x,y)

% ddf - filtered data densities at (x,y)

% radius - area used in 'circles' and 'squares'

% methods to calculate densities

% xi - x coordenates for zi matrix

% yi - y coordenates for zi matrix

% zi - unfiltered data densities at (xi,yi)

% zif - filtered data densities at (xi,yi)

% [c,h] = contour matrix C as described in

% CONTOURC and a handle H to a contourgroup object

% hs = scatter points handles

%

%Copy-Left, Alejandro Sanchez-Barba, 2005

if nargin==0

scatplotdemo

return

end

if nargin<3 | isempty(method)

method = 'vo';

end

if isnumeric(method)

gsp(x,y,method,2)

return

else

method = method(1:2);

end

if nargin<4 | isempty(n)

n = 5; %number of filter coefficients

end

if nargin<5 | isempty(radius)

radius = sqrt((range(x)/30)^2 + (range(y)/30)^2);

end

if nargin<6 | isempty(po)

po = 1; %plot option

end

if nargin<7 | isempty(ms)

ms = 7; %markersize

end

if nargin<8 | isempty(N)

N = 100; %length of grid

end

%Correct data if necessary

x = x(:);

y = y(:);

%Asuming x and y match

idat = isfinite(x);

x = x(idat);

y = y(idat);

holdstate = ishold;

if holdstate==0

cla

end

hold on

%--------- Caclulate data density ---------

dd = datadensity(x,y,method,radius);

%------------- Gridding -------------------

xi = repmat(linspace(min(x),max(x),N),N,1);

yi = repmat(linspace(min(y),max(y),N)',1,N);

zi = griddata(x,y,dd,xi,yi);

%----- Bidimensional running mean filter -----

zi(isnan(zi)) = 0;

coef = ones(n(1),1)/n(1);

zif = conv2(coef,coef,zi,'same');

if length(n)>1

for k=1:n(2)

zif = conv2(coef,coef,zif,'same');

end

end

%-------- New Filtered data densities --------

ddf = griddata(xi,yi,zif,x,y);

%----------- Plotting --------------------

switch po

case {1,2}

if po==2

[c,h] = contour(xi,yi,zif);

out.c = c;

out.h = h;

end %if

hs = gsp(x,y,ddf,ms);

out.hs = hs;

colorbar

case {3,4}

if po>3

[c,h] = contour(xi,yi,zi);

out.c = c;

end %if

hs = gsp(x,y,dd,ms);

out.hs = hs;

colorbar

end %switch

%------Relocate variables and place NaN's ----------

dd(idat) = dd;

dd(~idat) = NaN;

ddf(idat) = ddf;

ddf(~idat) = NaN;

%--------- Collect variables ----------------

out.dd = dd;

out.ddf = ddf;

out.radius = radius;

out.xi = xi;

out.yi = yi;

out.zi = zi;

out.zif = zif;

if ~holdstate

hold off

end

return

%~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

function scatplotdemo

po = 2;

method = 'squares';

radius = [];

N = [];

n = [];

ms = 5;

x = randn(1000,1);

y = randn(1000,1);

out = scatplot(x,y,method,radius,N,n,po,ms)

return

%~~~~~~~~~~ Data Density ~~~~~~~~~~~~~~

function dd = datadensity(x,y,method,r)

%Computes the data density (points/area) of scattered points

%Striped Down version

%

% USAGE:

% dd = datadensity(x,y,method,radius)

%

% INPUT:

% (x,y) - coordinates of points

% method - either 'squares','circles', or 'voronoi'

% default = 'voronoi'

% radius - Equal to the circle radius or half the square width

Ld = length(x);

dd = zeros(Ld,1);

switch method %Calculate Data Density

case 'sq' %---- Using squares ----

for k=1:Ld

dd(k) = sum( x>(x(k)-r) & x(y(k)-r) & y

end %for

area = (2*r)^2;

dd = dd/area;

case 'ci'

for k=1:Ld

dd(k) = sum( sqrt((x-x(k)).^2 + (y-y(k)).^2) < r );

end

area = pi*r^2;

dd = dd/area;

case 'vo' %----- Using voronoi cells ------

[v,c] = voronoin([x,y]);

for k=1:length(c)

%If at least one of the indices is 1,

%then it is an open region, its area

%is infinity and the data density is 0

if all(c{k}>1)

a = polyarea(v(c{k},1),v(c{k},2));

dd(k) = 1/a;

end %if

end %for

end %switch

return

%~~~~~~~~~~ Graf Scatter Plot ~~~~~~~~~~~

function varargout = gsp(x,y,c,ms)

%Graphs scattered poits

map = colormap;

ind = fix((c-min(c))/(max(c)-min(c))*(size(map,1)-1))+1;

h = [];

%much more efficient than matlab's scatter plot

for k=1:size(map,1)

if any(ind==k)

h(end+1) = line('Xdata',x(ind==k),'Ydata',y(ind==k), ...

'LineStyle','none','Color',map(k,:), ...

'Marker','.','MarkerSize',ms);

end

end

if nargout==1

varargout{1} = h;

end

return

3. 结果