深蓝学院的三维点云课程：第一章

一、前言

为什么现在点云应用这么广泛，就是因为他有深度信息。

像人脸识别用来解锁手机，比如Iphnoe手机在前边有一个深度摄像头，所以它产生的点云真的是一个三维点云；然后很多手机他可能就没有深度摄像头，它产生的就是一个图像，所以有的时候我们就可以使用一张照片就能骗过Arnold手机，但是很难用照片去骗过Iphone手机，因为Iphone他用的是三维信息也就是点云。所以这就是点云为什么会这么广泛的被应用起来，因为他有深度信息。

PS：激光雷达获取数据的特点是近密远疏。

点云形式：

我们有N个点，每个点有XYZ三个坐标，那么很显然他就是一个的matrix矩阵了，当然我们也可以加一些额外的信息，每个点加一些颜色信息或者有一些法向量之类的。

点云他就是一个矩阵。

点云可以从激光雷达中获取，RGBD相机中获取，获取其他的方式。

三维信息的表达形式：Mesh(三角形)：三角形结构太复杂、Voxel Grid()：规整的正方体比较的简单，但是他并不是很高效，因为我们的三维空间大部分都是空的，我们为一个空的空间，放这么多格子是一种对储存空间的内存浪费、Octree(八叉树)：他解决的效率的问题，因为他只是在有物体的地方才会去细分每一个正方体，所以他的内存占用会少很多，代价就是这个的表达形式比较复杂，不是很好用。

  

from flann import...

Nearest Neighbor Search//用来做点云的最邻近搜索

点云的难点在：

（1）密度的问题。（尤其在激光雷达里边近处的物体会反射很多个点，远处的物体就非常稀疏，导致难以识别。）

（2）不规则。（图像的每一个像素都是排成一个很规整的网格，所以我要找一个像素的邻居，只需要上下左右一格就找到了，但是对于点云很难找到离一个点最近的另外一个点；或者一个点一个半径范围内的邻居也是很难的）

（3）没有纹理信息。（比如在自动驾驶里边三人并排走在一起就会可能被识别为一个车。）

（4）Un-ordered问题。对于深度学习而言，他输进去的矩阵是不一样的，就会产生不一样的输出，但我们希望输出是一样的，这个就是深度学习的Un-ordered问题。（如何用深度学习去处理这种顺序有关系的一些数据）

（5）Rotation旋转问题。我们去旋转这些点，我们知道他还是同一个物体，但是他的坐标是完全不一样的。

偏slam就要算旋转平移矩阵了。

  

二、PCA & Kernel PCA

2.1、PCA介绍

PCA(Principle Component Analysis)：主成分分析。下面是二维和三维下的主成分分析图：

主成分分析的物理意义：主成分就是我先把这些数据点都投影到一个非常有特征性的方向上，然后每一个数据点在这个方向上的投影就是主成分。在三维情况下这个椭圆的主成分就是他的三个轴。

主成分的应用：

（1）降维（比如说上图中这些二维的点，如果我只把他投影到x plus上的话，他就变成了一维数据，而且这些一维数据最大程度上保全了这些点的原始信息就是沿着轴的分布，就是降维）

（2）法向量的估计（其实跟PCA是同一个应变量变，用的方法是一样的，）

（3）PCA可以用来作分类。

2.2、数学基础

向量的内积就是点乘（就是把其中一个向量投影到另外一个向量上去）。

一个矩阵与一个向量的乘法其实就是对这个矩阵的每一列进行一个线性的组合。

从SVD的角度去理解物理意义：比如说上图中的矩阵M，他可以被分解成   其中和V都是一个正交矩阵(类似于旋转矩阵的东西)，就是一个对角阵，他的对角线上储存了M的特征值，如果我把M乘以一个向量，第一步其实就是应用V在高维空间对这个向量做一个旋转，第一步这个圆被旋转了一下；第二步就是对这个旋转后的向量在每一个维度上做一个缩放，所以这个圆就变成了一个椭圆；第三步：再应用，也是高维空间上的旋转矩阵，所以我就把这个椭圆给旋转了一下。所以最后M乘以一个向量就是把这个圆变成了椭圆。

旋转矩阵就是正交矩阵。旋转矩阵是一个完美的矩阵——正交矩阵。

Q：旋转矩阵一定是正交矩阵，是对的。反过来正交矩阵一定是旋转矩阵，对吗？

A：不对。正交矩阵也可能是反射矩阵，不一定是旋转矩阵。

单位正交矩阵，且行列式为1，即是旋转矩阵。一个行列式为1的正交矩阵称为旋转矩阵。https://zhuanlan.zhihu.com/p/143056551

正交阵：https://www.cnblogs.com/caster99/p/4703033.html

https://blog.csdn.net/zhang11wu4/article/details/49761121

https://blog.csdn.net/mightbxg/article/details/79363699

Spectral Theorem(谱定理)：

有一个对称矩阵A，他可以被分解为   ，（就跟上边的SVD是一样的，但是因为A是一个对称矩阵，所以左右的两个是同一个，）。就是A的特征值，

如果矩阵的各列向量都是单位向量，并且两两正交。那么就说这个矩阵是正交矩阵。（参考xyz三维空间, 各轴上一个长度为1的向量构成的矩阵）

正交矩阵：https://zhuanlan.zhihu.com/p/258464098?utm_source=wechat_session

https://www.doc88.com/p-7844806191895.html

Rayleigh Quotients(瑞利熵)：

是一个向量，就是这个向量的模，就是在中间插入了一个对称矩阵A，之后就可以取得最大最小值。可以从SVD的物理意义去解释这个事情，如果我把这个A应用到这个向量上边去，那么其实就是对他做一些旋转缩放。这个特征值就是对这个向量的缩放，因为旋转不会改变向量的长度。

所以瑞利熵说的就是我这个A最终能够拉长或者缩短我这个向量多少倍，就是和是A的最小和最大特征值。

特征值分解只能针对于实对称矩阵，SVD分解是针对于任何矩阵的。每个实数矩阵都有一个奇异值分解，但不一定都有特征分解。例如，非方阵的矩阵没有特征分解，这是我们只能使用奇异值分解。特征值分解是一个提取矩阵特征很不错的方法，但是它只是对方阵而言的，在现实的世界中，我们看到的大部分矩阵都不是方阵，所以要用到奇异值分解。

https://blog.csdn.net/jcjunior/article/details/88064143

https://blog.csdn.net/lyxleft/article/details/84864791

是通过旋转一下，是通过对做一个高维的旋转，就是把它乘以一个，所以我们知道旋转是不会改变一个向量的长度的，所以这个的和和的和是一样的，

2.3、PCA讲解

2.3.1 概念：

PCA输入：PCA的输入是就是高维空间的一个向量，我们可以有m个向量，就是一堆高维空间中的点。

PCA输出：PCA的输出是一堆主要的向量。比如说就是他最主要的向量，描述了一群点里面最有代表性意义的高维的方向。 

Q：什么叫做最主要的成分？

A：其实就是说如果我把这个些高维点投影到某一个方向上，这些投影后的点方差要最大，就是说这些点在那个方向上，分布的非常的散。

Q：(假设我们已经得到了最主要的向量比如说)，我们如何得到 ？

A：就是我们先把这一组输入里边的属于的成分都去掉，然后我们再找剩下的东西里边的最主要的成分，就得到第二个。

Q：第三个最主要的成分怎么得到？

A：就是我把第二个最主要的方向的成分都去掉，同上就可以了。

  

2.3.2 PCA证明

• （1）首选i我们先把这一堆点，做个Normalize，把他的平均值设成0，也就是减去平均值，因为我们关心的是方向，所以他中心点在哪里对我们并没有太大关系，把它设为0。
• （2）然后PCA最主要的方向定义就是说这些点投影到一个方向上面，他的方差最大，所以那我就先投影，投影就是两个向量的内积，所以我们把每一个数据点把它投影到上边去，就得到一个，就是我这个点投影到方向上有多长，就是。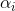
• （3）然后说PCA要算方差，那我就算方差，因为我们在（1）中已经减掉了一个mean,那方差就是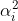的平方的和，最后再写成矩阵的形式。PCA要干的事情就是找到方差在某一个方向上的最大值，也就是它的最大值。这个与之前的瑞利熵很相似。
• （4）最后我们直接用瑞利熵的定义就可以得到方向到底是个什么样的东西。
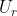
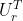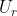• （5）所以用一下瑞利熵和谱定理，把这个H分解成   ，然后最主要的向量这里就是，然后就是的第一列。
• （6）因为我们可以用SVD的形式再去分解一下这个H。为什么我们要写成SVD的形式，因为下面我们就可以使用SVD的形式去求第二个最主要的方向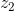。我们已经得到了最主要的方向，求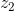的时很简单，把这些数据点里面属于的成分给去掉，什么叫做的成分呢？就是我把每一个数据点投影到这个方向去，然后再把数据点减掉这个的成分就好了，然后把它再写成矩阵的形式。
• 然后重新用SVD和的形式来看一下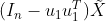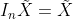，，因为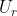其实是一个旋转矩阵就是正交矩阵，他的每一列都是互相垂直的，所以中间的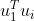除了i等于1的情况下都等于0。

总结：如果我们有一堆输入的点，每一个点都在n维空间，做PCA就是：

• 第一步：就是减掉这些数据点的中心。
• 第二步就是做H这个矩阵的SVD找到他的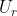，那么他的第一个主向量就是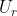的第一列，第二个主向量就是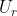的第二列，以此类推。
• PCA可以把他理解为基地的置换过程，就是我有一堆高维的数据点，然后如何去找出一组基底，使得第一个基底就是最有代表性的方向，也就是说他在这个基底的方向上分布的最广；然后第二个基底当然就是垂直与第一个基底的另外一个方向了，以此类推。所以PCA可以理解为一个基底的置换过程。 

2.3.3PCA的应用

第一个应用在降维上：

我们有一堆n维(n可能很大)数据点，使用一种办法把这个高维(就是n维)数据点投影到一维空间里边去，而且尽可能的保留他的特征；

办法就是：我们先用PCA找到他的个主向量，那么我就得到了个，这时候我们就把分别投影到每一个上边去，就可以得到了每一个在每一个方向上的投影，所以我们最后得到的每一个就是每一个向量在每一个方向上投影的成分，所以一个n维的点其实可以用一个维的这个系数来代替。再如何从维重新回到n维呢？就做一个和就行了，其实这个a就是每一个x在z上边的投影，那么我就把这个投影重新加起来就行了，当然我们经过了降维再升维肯定会有数据上的损失，除非我之前的l等于n，那么他就是一个完整的基地置换过程，不会是损失任何的信息，只要l是小于n的就会产生数据的损害，但是因为我们的这些主向量都是经过精心挑选的，所以他的数据的损失会比较小。

PS：Google了解一下Eigenfaces。

PCA的python实现：

##Python实现PCA
import numpy as np
def pca(X,k):#k is the components you want
  #mean of each feature
  n_samples, n_features = X.shape
  mean=np.array([np.mean(X[:,i]) for i in range(n_features)])
  #normalization
  norm_X=X-mean
  #scatter matrix
  scatter_matrix=np.dot(np.transpose(norm_X),norm_X)
  #Calculate the eigenvectors and eigenvalues
  eig_val, eig_vec = np.linalg.eig(scatter_matrix)
  eig_pairs = [(np.abs(eig_val[i]), eig_vec[:,i]) for i in range(n_features)]
  # sort eig_vec based on eig_val from highest to lowest
  eig_pairs.sort(reverse=True)
  # select the top k eig_vec
  feature=np.array([ele[1] for ele in eig_pairs[:k]])
  #get new data
  data=np.dot(norm_X,np.transpose(feature))
  return data
 
X = np.array([[-1, 1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
 
print(pca(X,1))

结果：

   

搞了半天结果不是很一样啊！分析一下吧！

sklearn中的PCA是通过svd_flip函数实现的，sklearn对奇异值分解结果进行了一个处理，因为ui*σi*vi=(-ui)*σi*(-vi)，也就是u和v同时取反得到的结果是一样的，而这会导致通过PCA降维得到不一样的结果（虽然都是正确的）。

用sklearn的PCA与我们的PCA做个比较：（结果见上图右）

##用sklearn的PCA
from sklearn.decomposition import PCA
import numpy as np
X = np.array([[-1, 1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
pca=PCA(n_components=1)pca.fit(X)
print(pca.transform(X))

参考链接：https://blog.csdn.net/program_developer/article/details/80632779?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522159046726919725256729568%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=159046726919725256729568&biz_id=0

https://blog.csdn.net/qq_45269116/article/details/106353433

2.4、Kernel PCA讲解

上述普通的PCA其实是一个线性的PCA，因为所谓的矩阵乘法也是一个线性操作而已，因为矩阵乘以向量其实是对矩阵列的线性组合，所以我们遇到的数据如果不是线性的。

定义一个函数φ，把二维的给提升为3维的，第三个维度选择两个坐标的平方和（其实就是极坐标的意思，因为他就是原来的点距离坐标原点的距离），变成三维空间之后呢我们就可以找到一个线或者平面把数据区分开，即这个时候只需要做一个普通的线性PCA就能够实现把红色绿色给分离开，只是这个时候是在三维空间不是在原来的二维空间。

升维操作：将原来二维空间的数据，升到三维空间，再做以划分。这个升维操作就叫做Kernel PCA。

步骤：

• 把原来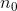维度的数据，通过函数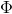给提升为。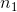
• 然后得到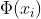之后，后边的操作和线性PCA是一模一样的(唯一的区别就是我们现在是在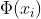上工作)。
• （1）之后先把他变成平均值为0。
• （2）算一下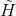矩阵。
• （3）要解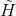他的特征值和特征向量。

难点：1、怎么选取这个升维函数；2、有时间升维之后的数据会非常的高，比如说我们的一个图片可能就是一个30x30的那么他就是一个900维或者更高维度的向量，那么这个时候在高维空间里边做矩阵的运算是非常耗费运算能力的，所以需要避免这种高维的操作，节省一下运算资源。这就是为什么提出了核PCA，我们就可以避免这种高维的操作，也可以更容易的选择这个升维函数。

第一步：给出一个结论就是这个特征向量可以表达成数据点的线性组合。是系数，就是映射到高维中的数据点。scalar表示标量，一个数字。

就是原来我们是在解这个特征向量的，但是现在我们可以把他看成是找一些系数，只要我们找到了这些系数，实际上我们就找到了这些特征向量。

核函数其实就是高维空间的一个内积，。这里还有两个和未被解决掉，因为我们不知道这个核函数长什么样子，所以暂时还不能用它。

KPCA举例：

选择二次多项式作为核函数，我们就可以得到不同的主成分，横轴是First component就是我们算出来的第一个主向量，我们把原来的数据投影到第一个主向量上面，得到一个数字，这个数字就是数据点在新的方向上的数值；Y轴是Second component就是第二个主成分，我把我的数据点投影到第二个主向量上边去就可以得到一个数值，我们可以看到只需要投影到第一个主成分上边去绿色蓝色和红色就已经很明显被分开了。

也可以是通过使用其他核函数，比如说这里使用高斯核函数，同样的X轴就是的第一个主成分，就已经非常好的把3种颜色给区分开了，