【AI100篇经典论文】Do ImageNet Classifiers Generalize to ImageNet

前情提要

在本论文当中，主要使用进行对比的数据集为ImageNet和CIFAR-10，在这两种数据集上选择合适的ImageNet来进行训练、测试。而为了体现训练后的泛化性如何，该论文中为这两种数据集建立了新的测试集进行另外的测试操作。

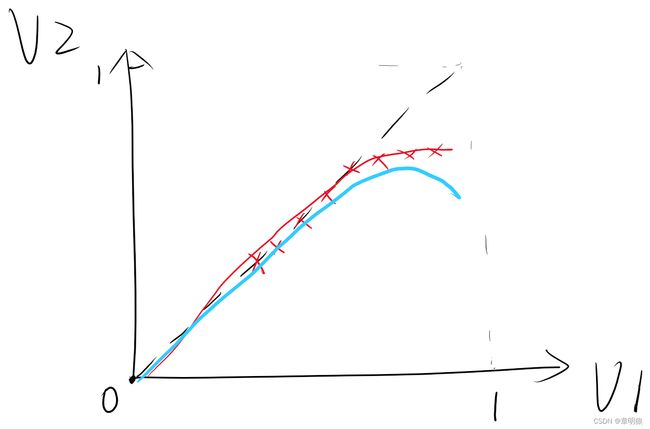
上述说法正如上图所示

V1表示在原有的ImageNet和CIFAR-10的数据集中，完成相关测试所得的正确率

V2表示在新的测试集中，完成相关测试所得的正确率

我们通常性的认为当我们在训练好的模型上进行验证时，当我们不断地增加训练次数epoch时，对于原有的数据集因为重复性的使用，而导致出现过度拟合overflow的风险增加。

正如上图中红线：V1的正确率增加，但对于V2的正确率基本不再变化。当然也有可能出现蓝线的情况，随着V1的正确率的不断上升，反而对于V2正确率有下降趋势。

主要结果

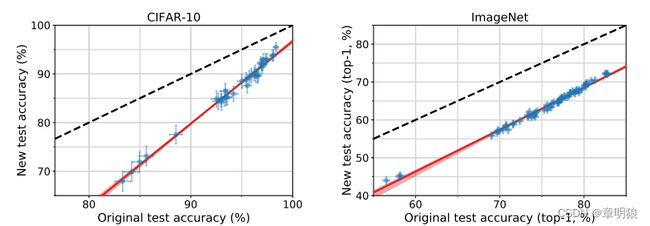
图1：是该论文主要的结果展示，为了支持未来的研究，团队已发布新的测试集和相应代码，其中新CIDFAR-10和新ImageNet【点击】

图1：原始测试集与我们的新测试集的模型准确性。

每个数据点对应于在我们的测试床中的一个模型(显示了95%的Clopper-Pearson置信区间)。

绘制这两个图时，它们的纵横比是相同的，即线的斜率在视觉上是可比较的。红色阴影区域是来自100，000个引导样本的线性拟合的95%置信区域。

这些图揭示了两个主要现象:

（1）从原始到新的准确性有显著下降测试集。

（2）模型精度严格遵循斜率大于1的线性函数(CIFAR-10为1.7，ImageNet为1.1)。这意味着原始测试集上的每一个百分点的进展都会转化为新测试集上的不止一个百分点。

从上面的图和上述分析可知：

（1）相同的分类模型下，当原测试集V1的准确性增高时，新的测试集进行准确性计算也会有增加的趋势，且呈线性增长的形式。

（2）从原始到新的准确性的线性值相较于同等线下降了（之间的差距解释如下部分）

简要分析

在采用标准分类器设置，并假设在标记的示例$(x，y)$上存在“真实的”潜在数据分布 $D$。

分类器的总体目标是找到一个模型$f$能够使得总体损失最小化。

由于我们通常不知道该分布，因此我们通过从该分布$D$中抽取的测试集 $S $来测量训练好的分类器的性能。

lassifiers Generalize to ImageNet【解读笔记】.assets/image-20220709110815784.png)]

基于上述两个公式，提出假设：将测试误差$L_S(\hat{f})$作为总体损失$L_D(\hat{f})$的代理，如果模型$\hat{f}$取得了较低的测试误差，我们就假设它将在分布的未来样本中表现得同样好。

• 这个假设基本上是机器学习中所有经验评估的基础，因为它允许我们认为模型是一般化的。

在这个实验中，我们通过从一个数据分布 $D^{\prime }$ 中收集一个新的测试集$S^{\prime }$来测试这个假设，我们 小心地控制这个数据分布$D^{\prime }$使其与原始分布$D$相似。

理想情况下，原始测试准确性$L_S(\hat{f})$和新测试准确性 $L_{S^{\prime }}(\hat{f})$将与随机采样误差相匹配。（如前情提要所述）

与这种理想化的观点相反，结果如图 1 显示从原始测试集 $S$到我们的新测试集 $S^{\prime }$ 的准确度有很大的下降。（在主要结果展示部分进行了相关介绍）

为了更详细地理解这种精度下降，我们将 $L_S(\hat{f})$和 $L_{S^{\prime }}(\hat{f})$之间的差异分解为三个部分

(简化符号，不再依赖 $\hat{f}$):

现在讨论这三项差距【适应性差距Adaptivity Gap】【数据分布差距Distribution Gap】【泛化性差距Generalization Gap】中的每一项会在多大程度上导致精度下降。

泛化性差距Generalization gap

在之前的构造中，新测试集$S^{\prime }$独立于现有的分类器$\hat{f}$。因此，第三项$L_{D^{\prime }}-L_{S^{\prime }}$是 机器学习中通常研究的标准泛化差距。它仅由随机采样误差决定。

第一种猜测是，这种固有的采样误差足以解释图中的精度下降 1（例如，新的测试集$S^{\prime }$可以更频繁地对分布$D$的某些“特殊”模式进行采样）。然而，对于新测试集的规模来说，这种量级的随机波动是不太可能的。（具体原因由选择的95%置信空间的大小差距变化为$\pm 1\%$，即使选择的是99.99%置信空间的大小差距变化也最多为$\pm 2$）

说明对于更高的精度，这些置信区间变得更小，这是最佳性能模型的相关机制。

因此，单凭随机机会无法解释我们实验中观察到的准确度下降。

适应性差距Adaptivity Gap

我们称$L_S-L_D$为适应性差距。它测量模型在多大程度上适应了测试集 $S$，从而导致测试误差 $L_S$ 低估了总体损失$L_D$，但是这种假设被直接在测试 集上调整模型超参数的常见做法破坏了，这在模型 $\hat{f}$和测试集 $S$之间引入了依赖性，在极端情况下，这可以被视为直接在测试集上训练。但是较温和形式的适应性也可能通过增加 $L_S$和$L_D$之间的差距，使其超出纯粹的随机误差，从而人为地夸大准确度分数。

分布差距Distribution Gap

称$L_D-L_{D^{\prime }}$为分布差距，它量化了从原始分布到新分布的变化对模型$\hat{f}$的影响程度。虽然过程中竭尽全力将这种系统差异最小化，但实际上很难争论两个高维分布是否完全相同。我们通常缺乏对这两种分布的精确定义，并且收集真实数据集涉及过多的设计选择。

区分两种机制

对于单个模型来说，不清楚如何理清适应性和分布差距。为了获得更细致的理解，我们测量了多个模型$f_1,...,f_k$这提供了额外的见解，因为它允许我们确定这两个差距是如何随着时间的推移而演变的。

对于 CIFAR-10 和 ImageNet 来说，分类模型都来自于一长串论文，这些论文在过去十年中逐步提高了准确率。一个自然的假设是，后来的模型经历了更多的自适应过拟合，因为它们是在同一测试集上更连续的超参数调整的结果。它们更高的准确性分数将来自于不断增加的适应性差距，并 且只反映了测试集$ S$ 中特定例子的进展，而不是实际分布的进展。在一个极端的情况下，总体准确性$L_D(\widehat{f_i})$将趋于平稳(甚至下降)，而连续模型$\widehat{f_i}$的测试准确性$L_S(\widehat{f_i})$将继续增长。

然而，这个理想化的场景与我们在图1中的结果形成了鲜明的对比，与早期模型相比，后来的模型没有看到收益递减，而是增加了优势。因此，我们将我们的结果视为准确性下降主要源于大的分布差距的证据。

其他变量和公式简述

图2：MTurk中分类进行的选择频率

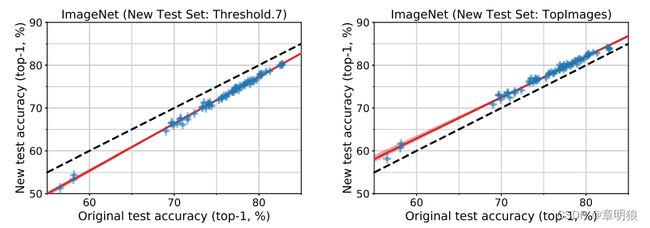
匹配频率MatchedFrequency：首先，我们从带注释的原始验证图像中估计每个类的选择频率分布。然 后，我们根据这些特定于类别的分布，从每个类别的候选池中抽取 10 幅图像进行采样。

Threshold0.7：对于每个类别，我们以至少 0.7 的选择频率采样 10 幅图像。

TopImages：对于每个类别，我们选择了 10 幅选择频率最高的图片。

图3绘制了Threshold0.7和TopImages的新准确性与原始准确性的对比，与图类似 1代表之前匹配的频率。所有三个图都显示了良好的线性拟合。

图3：Threshold0.7和TopImages的新准确性与原始准确性的对比

图3原始ImageNet验证集的模型准确性与新测试集的两个变体的准确性。每个数据点对应于我们测试平台中的一个模型(显示为95%的Clopper-Pearson置信区间)。在阈值为0.7时，模型精度比原始测试集低3%。在包含MTurk工作者最常选择的图像的TopImages上，模型的性能比原始测试集好2%。两个数据集的精度都严格遵循线性函数，类似于图1中的MatchedFrequency。红色阴影区域是来自100，000个引导样本的线性拟合的95%置信区域。

另一项有意思的实验

将V1与V2都划分为训练集和测试集，其中将两者的训练集放在一起进行训练，得到的模型对V2的测试集进行准确性的测试，发现准确性提高了。

有意思的建议对于未来的数据集

简单来说就是：以后的数据集设置，除了公布的数据集之外，都能将保留一个“不外露”的测试数据，在一段时间后，对现有训练的模型进行测试，来得到是否存在适应性过拟合的问题。

拜读原文点击：Do ImageNet Classifiers Generalize to ImageNet